Cám ơn Tuấn, xin trích dẫn lại lời giải của Telv ở #4 trong đây.

 

 

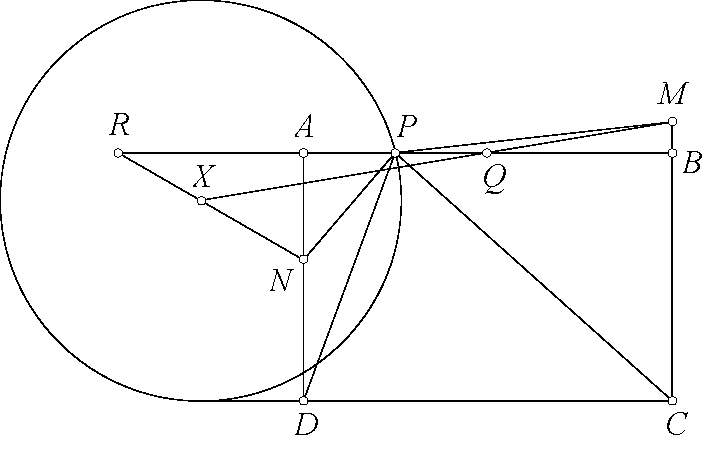
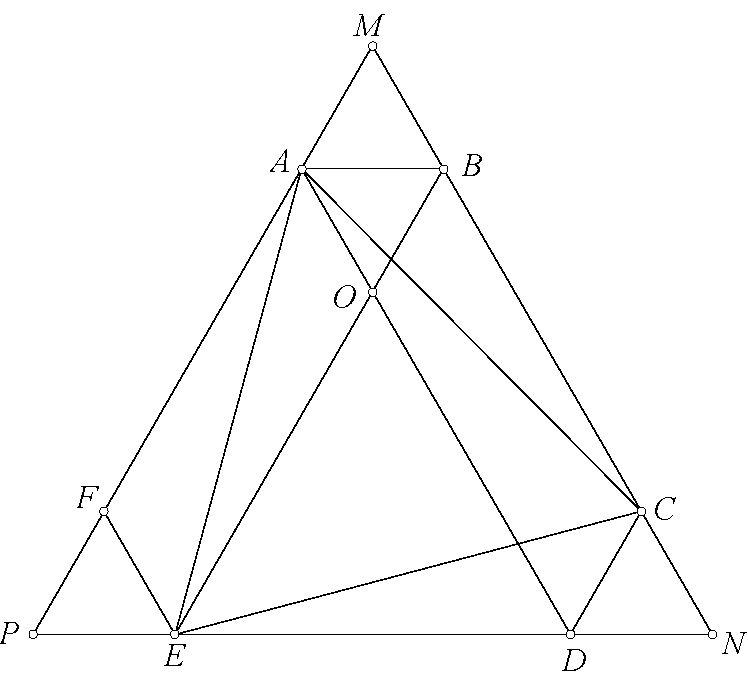
Giải bài toán 140 (Telv Cohl). Lấy điểm $Y$ sao cho hai tam giác $YBA$ và $XCD$ đồng dạng cùng hướng. Khi đó $\angle YAX+\angle YBX=\angle YAB+\angle BAX+\angle YBA+\angle ABX=\angle BAX+\angle XDC+\angle BAX+\angle XCD=180^\circ$. Từ đó $AYBX$ nội tiếp. Lại có $\angle YAB=\angle XDC=\angle XBA$ nên $AY\parallel BX$ do đó $AYBX$ là hình thang cân. Suy ra $AB^2=BY.AX+AY.BX$, lại có $YBA$ và $XCD$ đồng dạng nên $AB.CD=XA.XC+XB.XD$. Chứng minh tương tự $AD.BC=XA.XC+XB.XD$ nên $AB.CD=AD.BC$. Kết thúc chứng minh.

 

Bài toán 141. Cho bốn đường thẳng $\ell_1,\ell_2,\ell_3,\ell_4$ bất kỳ trong mặt phẳng. Gọi $H_1$ là trực tâm tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $P_1$ là cực trực giao của $\ell_1$ với tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $X_1$ thuộc $\ell_1$ sao cho $P_1X_1\perp P_1H_1$. Định nghĩa tương tự các điểm $X_2,X_3,X_4$. Chứng minh rằng $X_1,X_2,X_3,X_4$ đồng viên.

Đúng vậy, cám ơn Bảo dẫn lại link, xin dịch lại lời giải của Telv Cohl như sau

 

Giải bài toán 141 (Telv Cohl). Gọi $ V_{ij} $ ($ i, $ $ j $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ i $ $ < $ $ j $ $ \leq $ $ 4 $) lần lượt là giao điểm của $ \ell_i, $ $ \ell_j $ và gọi $ T $ là hình chiếu của $ V_{23} $ trên $ \ell_4. $ Ta biết rằng $ H_k, $ $ P_k $ ($ k $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ k $ $ \leq $ $ 4 $) nằm trên đường thẳng Steiner của tứ giác toàn phần tạo bởi $ \ell_1, $ $ \ell_2, $ $ \ell_3, $ $ \ell_4, $ và chú ý rằng $ T $ $ \in $ $ \odot (H_1P_4X_4) $ nên ta thu được (từ định lý Reim's) $ H_1, $ $ H_2, $ $ V_{34} $ $ X_4 $ Đồng viên. Tương tự ta có thể chứng minh $ X_3 $ nằm trên đường tròn này và $ H_1, $ $ H_3, $ $ V_{24}, $ $ X_2, $ $ X_4 $ cũng đồng viên, do đó ta thu được

 

$$ \measuredangle X_2X_4X_3 = \measuredangle X_2X_4H_1 + \measuredangle H_1X_4X_3 = \measuredangle X_2V_{24}H_1 + \measuredangle H_1V_{34}X_3 = \measuredangle (\ell_2, \perp \ell_3) + \measuredangle (\perp \ell_2, \ell_3). $$

 

Tương tự, ta có $ \measuredangle X_2X_1X_3 $ $ = $ $ \measuredangle (\ell_2, \perp \ell_3) $ $ + $ $ \measuredangle (\perp \ell_2, \ell_3), $ do đó chúng ta thấy rằng $ X_1, $ $ X_2, $ $ X_3, $ $ X_4 $ đồng viên.

 

Mình xin đề nghị bài tiếp cho topic tiếp tục.

 

Bài toán 142. Cho hình chữ nhật $ABCD$ và $P$ nằm trên cạnh $AB$. $Q,R$ đối xứng với $A,B$ qua $P$. Trung trực $PC,PD$ lần lượt cắt $BC,AD$ tại $M,N$. $MQ$ cắt $NR$ tại $X$. Chứng minh rằng đường tròn $(X,XP)$ tiếp xúc $CD$.

 

Cám ơn Khánh bài toán gốc ở đây phần chú ý trong #3 tại đây và lời giải ở trong #4, xin trích lại lời giải của Luis González

 

Lời giải khác bài toán 129. Gọi các tiếp tuyến của $(ABC)$ cắt nhau tại $A',B',C'$. Chú ý $\angle ACE=\angle ACX=\angle ABZ=\angle ABF$ và $\angle ACB'=\angle ABC,$ $\angle ABC'=\angle ACB$ nên $C(Y,E,B,B')=B(Z,F,C,C')$ suy ra $B(Y,E,C,B')=C(Y,E,B,B')=B(Z,F,C,C')=C(Z,F,B,C')$. $Q \equiv BY \cap CZ,$ $P \equiv BE \cap CF$ và $K \equiv BB' \cap CC'$ thẳng hàng.

 

Mình xin đề nghị bài tiếp.

 

Bài toán 130 (Từ đề thi Ba Lan). Cho lục giác $ABCDEF$ có các cạnh bằng nhau và $\angle A+\angle C+\angle E=\angle B+\angle D+\angle F$. Chứng minh rằng $AD,BE,CF$ đồng quy.

Cám ơn Khánh đã dẫn lại link. Gốc gác bài toán 128 là mình tổng quát hóa tính chất điểm Prasolov http://www.artofprob...h453505p2549205 và đã post nó ở đây http://www.artofproblemsolving.com/community/c6h455311. Như vậy là Bảo đã đưa ra tổng quát hơn nữa rất thú vị. Vậy nhờ Bảo dịch lại đáp án của mình sang tiếng Việt và post lên điên đàn. 

 

Mình đã nhận được ảnh từ bạn Đỗ Hoàng Việt lời giải cho bài toán 127 bằng hình học không gian thú vị, xin đăng lại ảnh đó, nhưng lưu ý bạn cần dùng latex và nên gõ lại đáp án cẩn thận.

 

 

Mình xin đề xuất bài mới.

 

Bài toán 129 (AoPS). Cho tam giác $ABC$. $D$ và $X$ lần lượt nằm trong và nằm ngoài tam giác sao cho $\angle DBC=\angle DCB=\angle XBC=\angle XCB=\theta$. Dựng tương tự các điểm $E,F,Y,Z$. Ta biết rằng $AD,BE,CF$ đồng quy tại $P$ và $AX,BY,CZ$ đồng quy tại $Q$. Chứng minh rằng $PQ$ đi qua điểm cố định khi $\theta$ thay đổi. 

 

Đáp án bài toán 117. Gọi $BC,DE,AF$ cắt nhau tạo thành tam giác $MNP$. Vì tổng các góc của lục giác là $720^\circ$ nên $\angle A+\angle B=\angle C+\angle D=\angle E+\angle F=240^\circ$. Vì vậy, ta dễ thấy tam giác $MNP$ đều. Dựng tam giác đều $DEO$ với $O$ nằm trong lục giác. Ta thấy $EOAF$ và $DOBC$ đều là hình bình hành, nên $AB=EF=OA=CD=OB$, vậy $OAB$ là tam giác đều. Do đó, $\angle AFE+\angle BCD=\angle AOE+\angle BOD=360^\circ-60^\circ-60^\circ=240^\circ$. Nhưng do $\angle EDC+\angle BCD=240^\circ$. Từ đó suy ra $\angle AFE=\angle EDC$. Tương tự, $\angle EDC=\angle CBA$. Từ đó  $\angle B=\angle D=\angle F$. Ta có điều phải chứng minh.

Mình xin đề nghị bài toán tiếp

 

Bài toán 144. Cho tam giác $ABC$ với đường cao $AD,BE,CF$. Chứng minh rằng điểm Lemoine của tam giác $ABC$ là trọng tâm tam giác tạo bởi các điểm Lemoine của tam giác $AEF,BFD,CDE$.

Cám ơn em, xin dịch lại lời giải của bạn Đỗ Xuân Long đưa ra tại đây

 

Gọi $X,Y,Z$ là điểm Lemoine của các tam giác $AEF,BDF,CDE$. $H,O,G,L$ là trực tâm, tâm ngoại tiếp, trọng tâm, điểm Lemoine của tam giác $ABC$. $M, N$ là trung điểm của $BC, EF$. $T$ là trung điểm $AD$. $AU\perp EF$. $V$ là trung điểm $AU$. ta biết rằng $MT$ đi qua $L$. Từ $AU\parallel MN$, ta có $\frac {XA}{XM}=\frac {XV}{XN}=\frac {LT}{LM}$ vì vậy nên $XL\parallel AH \implies XL\perp BC$. Từ $\triangle DYZ\sim \triangle HBC$, ta thấy $AM\perp YZ \implies GX\perp YZ$. Gọi $\ell$ là đường thẳng qua $X$ và song song $YZ$. $t$ là đường thẳng qua $G$ và vuông góc $AD.$ Ta có $X(L,\ell,Y,Z)=G(M,t,BC)=-1$, nên $XL$ chia đôi $YZ$. Tương tự thì $L$ là trọng tâm tam giác $XYZ$.

 

Mình xin đề nghị bài tiếp.

 

Bài toán 145 (AoPS). Cho tam giác $ABC$ với $\angle BAC<45^{\circ}$. $D$ ở trong tam giác $ABC$ sao cho $BD=CD$ và $\angle BDC=4\angle BAC$. $E$ là đối xứng của $C$ qua $AB$. $F$ là đối xứng của $B$ qua $AC$. Chứng minh rằng $AD\perp EF$.

 

 

Lời giải bài toán 165. Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}$. Gọi phân giác $\angle BAC$ cắt $PQ$ tại $I$ do thì $\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$ nên $BI$ là phân giác $\angle ABC$. Từ đó $I$ là tâm nội tiếp và $CI$ là phân giác $\angle ACB$ đồng thời cũng là phân giác $\angle PCQ$ nên $\frac{CP}{CQ}=\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$, ta hoàn thành chứng minh.

 

Em đã viết ra và gửi thầy qua mail. Nhận xét của em đúng và lời giải thầy cần bổ sung thêm một đoạn cuối, cám ơn em. Thầy viết cẩn thận như sau

 

Lời giải bài toán 165. Khi $P=Q$ thì ta có kết luận hiển nhiên đúng.

 

Khi $P\not=Q$. Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}$. Gọi phân giác $\angle BAC$ cắt $PQ$ tại $I$ do thì $\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$ nên $BI$ là phân giác $\angle ABC$. Từ đó $I$ là tâm nội tiếp và $CI$ là phân giác $\angle ACB$ đồng thời cũng là phân giác $\angle PCQ$ nên $\frac{CP}{CQ}=\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$. Từ đó $(ABC)$ là đường tròn Apollonius của đoạn $PQ$ như vậy $I$ cũng nằm trên $(ABC)$ điều này vô lý.

Em viết rõ chỗ "kết hợp định lý Ceva dạng lượng giác suy ra "... thầy nghĩ chỗ đó có vấn đề.

Cám ơn các em đã đóng góp, các marathon olympic ở trên diễn đàn ai thích tham gia cái nào cứ thoải mái có vấn đề gì đâu. Mình xin đưa ra đáp án chi tiết cho bài toán 153.

 

 

Đáp án bài toán 153. Trước hết ta thất $BA=BM$ nên $\angle BCM=\angle BCA$ do đó $CM$ và $CA$ là hai đường thẳng đối xứng nhau qua $BC$. Tương tự $BN$ và $BA$ là hai đường thẳng đối xứng nhau qua $BC$. Xét đối xứng trục $BC$ thì $D,K$ lần lượt biến thàng $L,O$ và ta vẫn có $BL\parallel DC, CL\parallel DB$. Khi đó $E$ sẽ $U$ biến thành giao điểm của đường thẳng qua $O$ song song $BL$ và $AC$ hay cũng chính là giao của đường thẳng qua $O$ song song $DC$ và $AC$. Tương tự $F$ biến thàng $V$ là giao điểm của đường thẳng qua $O$ song song với $DB$ và $AB$. Qua đối xứng trục $BC$ thì $H$ biến thành $X$ là giao điểm của $AH$ và $(O)$. Theo bài toán Iran 2013, thì $XU=XV$. Qua đối xứng trục $BC$ cho ta $HE=HF$.

 

Bài toán 153 là một ứng dụng của bài toán Iran 2013, bài toán này đã được mình tổng quát trong đề thách thức toán học trên số 1 của tạp chi PI. Xung quanh bài toán này còn rất nhiều điểm thú vị.

 

Bài toán 146 mình gửi lên AoPS đã lâu, có thể coi là tổng quát của 2010 APMO P4 và 2012 China TST P3, các bạn có thể xem đề bài và đáp án tại đây trong #7 và #8. 

 

Xin đề nghị tiếp một bài nữa để topic được tiếp tục với 2 bài toán

 

Bài toán 155 (AoPS). Cho tam giác $ABC$. Đường tròn nội tiếp tiếp xúc $AB,BC$ tại $D,E$. Lấy điểm $F$ trên cạnh $AB$ sao cho $BF=AD$. Phân giác góc $\angle BCA$ cắt $AB$ tại $K$ và cắt đường tròn ngoại tiếp tam giác $CDF$ tại $L$ khác $C$. Đường tròn ngoại tiếp tam giác $EKL$ cắt $BC$ tại $N$ khác $E$. Chứng minh rằng tam giác $BNF$ cân.

 

 

 

 

Năm mới xin chúc các bạn mọi điều tốt đẹp như ý. Minh xin khai trương topic năm mới bằng cách giải bài này và đề nghị một bài đẹp tiếp theo  . Trước hết thay đổi một chút ký hiệu cho bài toán dễ nhìn.

 

Bài toán 152 (Dark Repulsor). Cho tam giác $ABC$ có đường cao $BE,CF$ cắt nhau tại $H$. $M,N$ là trung điểm của $CE,BF$. $HM,HN$ cắt các đường tròn $(HBF),(HCE)$ lần lượt tại $P,Q$ khác $H$. $U,V$ lần lượt thuộc $BE,CF$ sao cho $AU\perp AB,AV\perp AC$. Chứng minh rằng $PQ\parallel UV$.

 

 

Giải bài toán 152. Ta thấy $\angle MCH=\angle HBF=\angle HPF$ nên tứ giác $FMCP$ nội tiếp. Tương tự tứ giác $ENBQ$ nội tiếp. Từ đó $HP.HM=HF.HC=HE.HB=HN.HQ$, ta suy ra $MNPQ$ nội tiếp. Gọi $EF$ cắt $BC$ tại $G$. $GH$ cắt $CA,AB$ tại $L,K$. Ta thấy $(AK,FB)=(AL,EC)=-1$ nên $AL.AM=AE.AC=AF.AB=AK.AN$ suy ra $KLMN$ nội tiếp. Kết hợp $MNPQ$ nội tiếp suy ra $PQ\parallel KL\perp AR$ với $R$ là trung điểm $BC$. Gọi $D$ đối xứng $A$ qua $R$ thì dễ thấy hai tam giác $AUV$ và $CDA$ đồng dạng c.g.c lại có các cạnh $AV\perp AC, AU\perp CD$ nên $AD\perp UV$. Từ đó $PQ\parallel UV$ do cùng vuông góc $AD$.

 

Bài toán 153. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, trực tâm $H$ và $D$ là trung điểm của cung $BC$ không chứa $A$. $K$ là tâm ngoại tiếp tam giác $HBC$. $M,N$ lần lượt đối xứng $A$ qua $OB,OC$. Trên $MC,NB$ lần lượt lấy $E,F$ sao cho $KE\parallel DB,KF\parallel DC$. Chứng minh rằng $HE=HF$.

 

 

Lưu ý các bạn vẫn còn bài toán 146 chưa có lời giải.

Cám ơn Quân đã đóng góp lời giải, bài này thầy mở rộng từ bài IMO 2005, xin đề nghị bài tiếp như sau

 

Bài toán 118. Cho tam giác $ABC$ nhọn trực tâm $H$, tâm ngoại tiếp $O$, $G$ là trọng tâm của tam giác $HBC$. $K$ thuộc đoạn $AH$ sao cho $\angle BKC=90^\circ$. $KG$ cắt trung trực $BC$ tại $L$. Các điểm $P,Q$ thuộc đoạn $BC$ sao cho $LP\parallel OB,LQ\parallel OC$. Các điểm $E,F$ thuộc đường thẳng $HC,HB$ sao cho $PE,QF$ cùng vuông góc với $BC$. Chứng minh rằng $EF=PE+QF$.

Lời giải bài toán 112. Gọi tiếp tuyến qua $B,C$ của $(O)$ cắt nhau tại $S$. $TK$ tại $J$. Do $(K)$ tiếp xúc $(O)$ nên $KL\parallel AO$. Từ đó $\frac{JS}{XS}=\frac{KO}{XO}=\frac{LA}{XA}$ suy ra $\frac{JS}{LS}=\frac{XS}{LS}:\frac{XA}{LA}$. Ta thấy các hàng điểu hòa cơ bản $(AX,SD)=(AD,SL)=-1$ do dó $(AS,XD)=(AS,DL)=2$ suy ra $\frac{XA}{XS}:\frac{DA}{DS}=\frac{DA}{DS}:\frac{LA}{LS}=2$ từ đó dễ thấy $\frac{XS}{LS}:\frac{XA}{LA}=\frac{1}{4}$ hay $\frac{OT}{OL}=\frac{JS}{JL}=\frac{1}{4}$. Ta hoàn thành chứng minh.



Bài toán 113. Cho tam giác $ABC$ và $P$ bất kỳ. $D,E,F$ là hình chiếu của $P$ lên $BC,CA,AB$. $(DEF)$ cắt $BC$ tại $M$ khác $D$. $DP$ cắt $EF$ tại $L$. $AL$ cắt $BC$ tại $K$. Các đường thẳng qua $A,M$ lần lượt vuông góc với $BC,PK$ cắt nhau tại $X$. Chứng minh rằng $XK\parallel EF.$

Cám ơn Bảo, lời giải rất chuẩn, bài gốc thực chất không khó nhưng rất mới và đẹp, thầy rất thích những bài nhẹ nhàng và mới như thế ! Từ bài tổng quát thầy vẫn thử tìm tổng quát hơn cho đẳng giác bất kỳ mà chưa thu được gì ? 

 

Nếu Bảo đồng ý thầy sẽ bù lại một bài đỡ hơn ?

Lời giải không nghịch đảo của Khoa cho bài của thầy rất thú vị, bài đó thầy tạo ra từ nghịch đảo giống như Quân (halloffame) đã làm, bài toán gốc là một mở rộng của bài 4 trong IMO 2010, hãy đón đọc cả bài viết trong kỷ yếu GGTH 2016 !

Bài toán 43 gốc ở đây http://artofproblems...1198358p6114585 problem 13 của Telv Cohl.

 

Vừa rồi có 2 bài ELMO 2016 mới có trên mạng rất hay, nhờ cảm hứng bài này và được sự đồng ý của Dương, mình đề nghị bài sau

 

$\boxed{\text{Bài toán 44.}}$ Cho tam giác $ABC$ với $P$ là một điểm nằm trên trung trực $BC$ và $Q$ là đẳng giác của $P$ trong tam giác $ABC$. $PD$ là đường kính của đường tròn $(PBC)$. $QB,QC$ cắt đường tròn $(QCA),(QAB)$ tại $E,F$ khác $Q$. $K$ là tâm $(DEF)$. Chứng minh rằng $AK\perp BC$.

 

Cám ơn Bảo, lời giải rất hay khác với lời giải thầy biết, sau đây là link gốc của bài toán

 

http://www.artofprob...nity/c6h1144762

Được sự đồng ý của Dương, mình đề nghị hộ một bài toán

 

$\boxed{\text{Bài toán 39}}$ (Telv Cohl+Trần Quang Hùng). Cho tam giác $ABC$ và $P$ là một điểm trên đường tròn ngoại tiếp. $Q$ là hình chiếu của $P$ lên cát tuyến trực giao của $P$ ứng với tam giác $ABC$. Chứng minh rằng trực tâm các tam giác $APQ,BPQ,CQP$ cùng nằm trên đường thẳng $\ell$ và đường thẳng qua $P$ vuông góc với $\ell$ luôn đi qua điểm cố định khi $P$ thay đổi.

 

Khái niệm cát tuyến trực giao

Bài toán Gossard có thể tham khảo thêm các link sau từ AoPS

 

http://artofproblems...unity/c6h284982

 

http://artofproblems...unity/c6h561557

 

Được Dương đồng ý, mình xin đề nghị bài sau (Trong chuỗi bài GGTH 2016)

 

$\boxed{\text{Bài toán 51.}}$ Cho tam giác $ABC$ nhọn nội tiếp trong đường tròn $(O)$. $P$ là một điểm nằm trong tam giác và nằm trên trung trực $BC$. Lấy điểm $Q$ trên đường tròn $(PBC)$ và nằm trong tam giác sao cho $\angle PQA+\angle OAP=90^\circ$. $QA,QB,QC$ lần lượt cắt $BC,CA,AB$ tại $D,E,F$. $DE,DF$ lần lượt cắt $PQ$ tại $M,N$. Chứng minh rằng $BN,CM,EF$ đồng quy tại $R$ và $\angle RQA=\angle PAO$.

Đáp án gốc bài toán 71.



Gọi $ABC$ là tam giác nội tiếp đường tròn $(O)$ và điểm $P$ thuộc $(O)$. Để tiện cho theo dõi chúng ta giả sử $P$ thuộc cung $BC$ không chứa $A$. Gọi $E,F$ là hình chiếu của $P$ lên $CA,AB$ thì đường thẳng $EF$ là đường thẳng Simson của $P$ ứng với tam giác $ABC$. Gọi $M,N$ là hình chiếu của $C,B$ lên $EF$. Đường thẳng qua $M,N$ lần lượt vuông góc với $AB,AC$ cắt nhau tại $L$ thì $L$ chính là cực trực giao của $EF$ ứng với tam giác $ABC$. Ta sẽ chứng minh rằng $EF$ chia đôi $PL$, thật vậy. Gọi đường cao $CS,BT$ của tam giác $ABC$ cắt nhau tại $H$ và đường cao $EU,FV$ của tam giác $AMN$ cắt nhau tại $L$. Theo kết quả quen thuộc về đường thẳng Steiner thì $EF$ chia đôi $PH$, mặt khác dễ thấy $PEKF$ là hình bình hành nên $EF$ chia đôi $PK$ vậy ta sẽ chứng minh $H,K,L$ thẳng hàng thì $EF$ sẽ chia đôi $PL$. Ta xét các đường tròn đường kính $BE$ và $CF$. Ta dễ thấy $HB.HT=HC.HS$ và $KF.KV=KE.KU$ nên $H,K$ thuộc trục đẳng phương của hai đường tròn này. Gọi $UV$ cắt đường tròn đường kính $BE,CF$ tại $J,I$ khác $U,V$. Ta có $\angle UJN=\angle UEN=\angle EUF=\angle UVF$. Từ đó $NJ\parallel FV\perp AC$ nên $NJ$ đi qua cực trực giao $L$. Tương tự $MI$ đi qua $L$. Lại có $\angle IJN=\angle UVF=\angle UEF=\angle IMN$, suy ra tứ giác $MNIJ$ nội tiếp. Vậy $LI.LM=LJ.LN$ hay $L$ cũng thuộc trục đẳng phương của đường tròn đường kính $BE,CF$. Từ đó ta suy ra $H,K,L$ thẳng hàng hay $EF$ chia đôi $PL$.

 

Bài này chính xác là mình đã gửi đăng THTT, lời giải trên đó của Dương, vậy Dương có thể giới thiệu lời giải của mình lên đây được không ?

 

Topic đã qua một chặng đường lớn, mình rất vui vì topic ngày càng lớn mạnh và được nhiều bạn tận tụy tham gia đóng góp sức mình, mong rằng số bài sẽ nhanh cán mốc $100$.

Cám ơn Hoàng cho lời giải thú vị khác đáp án cho bài toán 102. Sau đây là đáp án của thầy. Phần đầu của chứng minh này có tham khảo trên AoPS nhưng mình không tìm lại link, xin trích dẫn sau.

 

 

Lời giải bài toán 102. Gọi $CI$, $BI$ lần lượt cắt đường tròn $(AIB)$, $(AIC)$ tại $I_c$, $I_b$ thì $I_c$, $I_b$ chính là các tâm đường tròn bàng tiếp góc $C$, góc $B$ của tam giác $ABC$. Do đó $I_c$, $A$, $I_b$ thẳng hàng. Mặt khác do $I_cB\parallel AK$, $BK\parallel AI_c$ nên $I_cAKB$ là hình bình hành từ đó $K$ đối xứng $I_c$ qua trung điểm $AB$. Tương tự thì $L$ đối xứng $I_b$ qua trung điểm $AC$. Gọi $E$, $F$, $H$, $N$ lần lượt là trung điểm $CA$, $AB$, $KL$, $I_cI_b$ thì $H$, $N$ đối xứng nhau qua trung điểm $EF$ nên $AH\perp BC$ hay $AH\parallel ON$. Gọi $M$ là trung điểm $BC$ thì $A$ đối xứng $M$ qua trung điểm $EF$. Do đó $AHMN$ là hình bình hành suy ra $AH=MN$ nên $AH$ có độ dài không đổi. $AP$ cắt $OM$ tại $Q$ thì tính chất đường trung bình cho ta $OQ=2AP$ suy ra $OQ$ không đổi hay $Q$ cố định. Vậy $AP$ đi qua điểm $Q$ cố định khi $A$ thay đổi.

 

 

Và lời giải bài 103.

 

 

Lời giải bài toán 103. Dễ thấy $AM$ là phân giác ngoài góc $\angle BAC$ nên $N$ là trung điểm cung $XY$ chứa $A$ của đường tròn $(K)$ ngoại tiếp tam giác $AXY$ nên trung trực $XY$ đi qua $N$. Dễ thấy trung trực $BC$ đi qua $M$. Gọi trung trực $BC$ và $XY$ cắt nhau tại $R$. Ta sẽ chứng minh tam giác $RMN$ cân thì trung trực $MN$ đi qua $R$, thật vậy. Gọi $AD$ là phân giác của tam giác $ABC$ dễ thấy $AD\perp MN$, ta có biến đổi góc. 

 

$$(RM,MN)=(BC,AD)=(BC,BP)+(BP,AD)=(QC,QP)+(AD,QC)=(PQ,AD)=(MN,RN)$$.

 

Từ đó tam giác $RMN$ cân tại $R$.

 

Bài toán 104 (Tập huấn đội IMO 2016, tập huấn đội KHTN 2017). Cho tam giác $ABC$ nhọn, nội tiếp đường tròn $(O)$. Phân giác $AD$, $BE$, $CF$. $X$, $Y$, $Z$ lần lượt là trung điểm cung $BC$ chứa $A$, cung $CA$ chứa $B$, cung $AB$ chứa $C$. Trung trực $CA$, $AB$ cắt $AZ$, $AY$ tại $A_1$, $A_2$. $U$ đối xứng $A$ qua $A_1A_2$. Tương tự có $U$, $W$. Chứng minh rằng tiếp tuyến qua $A$, $B$, $C$ của các đường tròn $(ADU)$, $(BEV)$, $(CFW)$ đồng quy.

 

 

Cám ơn Bảo về bài phát triển và lời giải hay, thầy đễ xuất bài sau

 

$\boxed{\text{Bài toán 92.}}$ Cho tam giác $ABC$ nhọn có tâm ngoại tiếp $O$, trực tâm $H$ và đường tròn Euler là $(N)$. Dựng hình bình hành $ABDC$. Trên trục đẳng phương của đường tròn đường kính $OD$ và $(N)$ lấy $P$ sao cho $OP\parallel BC$. $K$ thuộc $OH$ sao cho $PK=PO$. Chứng minh rằng trục đẳng phương của đường tròn đường kính $HK$ và $(N)$ đi qua $O$.

Cám ơn Dương, đáp án của thầy cũng là bổ đề đó. Bài này trông cấu hình có vẻ kinh khủng như khi giải ra cũng không phức tạp. Ý tưởng dựa vào bổ đề đẳng giác trên và bài này là đặc trưng cho góc định hướng.

Cám ơn Dương về lời giải mới chặt chẽ.

 

Lời giải nghịch đảo là cách mình tạo ra bài toán 73. Lời giải không nghịch đảo của Hoàng hay.

 

$\boxed{\text{Bài toán 74.}}$ Cho tam giác $ABC$ và $P,Q$ là hai điểm bất kỳ. Gọi $D$ là giao điểm của đối xứng $PB,PC$ lần lượt qua $QB,QC$. Tương tự có $E,F$. Gọi $K,L$ đẳng giác với $P,Q$ trong tam giác $ABC$. Gọi $X$ là giao điểm của đối xứng $KB,KC$ lần lượt qua $LB,LC$. Tương tự có $Y,Z$. Chứng minh rằng các đường tròn ngoại tiếp tam giác $DBC,ECA,FAB$ có điểm chung $S$, các đường tròn ngoại tiếp tam giác $XBC,YCA,ZAB$ có điểm chung $T$ và $S,T$ đẳng giác trong tam giác $ABC$.

 

Bài này là bài tập huấn đội KHTN năm 2016.

Cũng không vấn đề gì cả, mình sau này có thể tự nghĩ ra những bài đã có từ trước là chuyện rất bình thường, thầy đã bị thế nhiều. Bởi vậy việc đưa lên thảo luận là quan trọng vì nếu ai biết thì trích dẫn lại rõ ràng bài này đầu tiên có ở đâu để mình biết !