Chủ đề này có 11 trả lời

[cunshockbaby]

Đề thi vào lớp 10 môn toán THPT Chuyên Lam Sơn

File gửi kèm

•  Đề thi vào lớp 10 môn toán THPT Chuyên Lam Sơn.pdf   104.09K   1694 Số lần tải

[minhtuyb]

Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Ngày thi: 17 tháng 6 năm 2012

Câu 1: (2,0 điểm) Cho biểu thức:
$P=(\frac{\sqrt{a+1}}{\sqrt{a-1}}-\frac{\sqrt{a-1}}{\sqrt{a+1}}+4\sqrt{a})\frac{1}{2a\sqrt{a}}$ (với $a>;a\ne 1$)
1. Chứng minh rằng $P=\frac{2}{a-1}$
2. Tìm giá trị của $a$ để $P=a$

Câu 2: (2,0 điểm) Trong mặt phẳng tọa độ $Oxy$, cho Parabol $(P):y=x^2$ và đường thẳng $(d):y=2x+3$
1. Chứng minh rằng (d) và (P) có 2 điểm chung phân biệt
2. Gọi $A,B$ là các điểm chung của (d) và (P). Tính diện tích tam giác $OAB$

Câu 3: (2,0 điểm) Cho phương trình $x^2+2mx+m^2-2m+4=0$
1. Giải phương trình khi $m=4$
2. Tìm $m$ để phương trình có hai nghiệm phân biệt

Câu 4: (3,0 điểm) Cho đường tròn $(O)$ có đường kính $AB$ cố định, $M$ là điểm thuộc $(O)$ ($M$ khác các điểm $A,B$). Các tiếp tuyến với $(O)$ tại $A$ và $M$ cắt nhau ở $C$. Đường tròn $(I)$ đi qua $M$ tiếp xúc với đường thẳng $AC$ tại $C$; $CD$ là đường kính của $(I)$. Chứng minh rằng:
1. Ba điểm $O,M,D$ thẳng hàng
2. Tam giác $COD$ là tam giác cân
3. Đường thẳng đi qua $D$ và vuông góc với $BC$ luôn đi qua một điểm cố định khi $M$ di động trên đường tròn $(O)$

Câu 5: (1,0 điểm)
Cho $a,b,c$ là các số thực không âm thỏa mãn điều kiện: $a^2+b^2+c^2=3$.
Chứng minh rằng: $\frac{a}{2a^2+b+3}+\frac{b}{2b^2+c+3}+\frac{c}{2c^2+a+3}\le \frac{1}{2}$

----------------------------------Hết----------------------------------

(Cán bộ coi thi không giải thích gì thêm)

Bài viết đã được chỉnh sửa nội dung bởi minhtuyb: 17-06-2012 - 14:14

[danganhaaaa]

bài 5.
dễ thấy $\frac{a}{2a^{2}+2b+3}\leq \frac{a}{2a+2b+2}$ (bất đẳng thức cô si)
suy ra ta cần cm $\sum \frac{a}{2a+2b+2}\leq \frac{1}{2}\Leftrightarrow \sum \frac{a}{a+b+1}\leq 1$
lấy 3 trừ đi cả 2 vế của BĐT suy ra ta cần cm
$\sum \frac{b+1}{a+b+1}\geq 2 \Leftrightarrow \sum \frac{(b+1)^{2}}{(a+b+1)(b+1)}\geq 2$
áp dụng bất đẳng thức cauchy schwart suy ra ĐPCM (biến đổi hơi dài dòng mà lại ngại đánh latex)

Bài viết đã được chỉnh sửa nội dung bởi danganhaaaa: 20-06-2012 - 11:06

[nthoangcute]

dễ thấy $\frac{a}{2a^{2}+b+3}\leq \frac{a}{2a+2b+2}$ (bất đẳng thức cô si)
suy ra ta cần cm $\sum \frac{a}{2a+2b+2}\leq \frac{1}{2}\Leftrightarrow \sum \frac{a}{a+b+1}\leq 1$
lấy 3 trừ đi cả 2 vế của BĐT suy ra ta cần cm
$\sum \frac{b+1}{a+b+1}\geq 2 \Leftrightarrow \sum \frac{(b+1)^{2}}{(a+b+1)(b+1)}\geq 2$
áp dụng bất đẳng thức cauchy schwart suy ra ĐPCM (biến đổi hơi dài dòng mà lại ngại đánh latex)

Chỗ màu đỏ chứng minh như nào !!!

[danganhaaaa]

Chỗ màu đỏ chứng minh như nào !!!

tớ chép nhầm đề rồi!!!thông cảm!!!

[nthoangcute]

Câu 5: (1,0 điểm)
Cho $a,b,c$ là các số thực không âm thỏa mãn điều kiện: $a^2+b^2+c^2=3$.
Chứng minh rằng: $\frac{a}{2a^2+b+3}+\frac{b}{2b^2+c+3}+\frac{c}{2c^2+a+3}\le \frac{1}{2}$

Giải như sau:
Áp dụng BĐT Cô-si ta có:
$2a^2+b+3 \geq 4a+b+1$
Suy ra $$\sum \frac{a}{2a^2+b+3} \leq \sum \frac{a}{4a+b+1}$$
$$=\frac{3}{4}-\sum \frac{b+1}{4(4a+b+1)}$$
$$\leq \frac{3}{4} - \frac{(a+b+c+3)^2}{4 \sum (a+1)(4c+a+1)} $$
$$=\frac{3}{4}- \frac{a^2+b^2+c^2+2(ab+bc+ca)+6(a+b+c)+9}{4(a^2+b^2+c^2+4(ab+bc+ca)+6(a+b+c)+3)} $$
$$\leq \frac{3}{4} -\frac{a^2+b^2+c^2+2(ab+bc+ca)+6(a+b+c)+3+2(ab+bc+ca)}{4(a^2+b^2+c^2+4(ab+bc+ca)+6(a+b+c)+3)}=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}$$
Suy ra đpcm

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 18-06-2012 - 12:08

[dangthettbn]

bai hinh phan 3, to tim dc diem co dinh roi nhung chua cm dc, ai lam ho cai

[sherry Ai]

bai hinh phan 3, to tim dc diem co dinh roi nhung chua cm dc, ai lam ho cai

giống tớ thế

[perfectstrong]

Câu 4: 3)

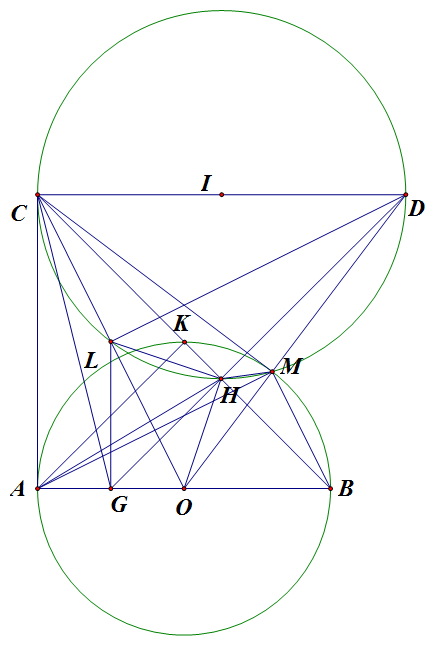
Vẽ $OC$ cắt $(I)$ tại điểm thứ 2 là $L \Rightarrow \angle DLC=90^o \Rightarrow DL \perp OC$
Mà $\vartriangle DOC$ cân tại $D$ nên $L$ là trung điểm $OC,(1)$.
$\angle MHB=\angle MDC=\angle MOB \Rightarrow HMBO:tgnt$
$\Rightarrow \angle OHB=\angle OMB=\angle OBM=\angle AOC=\angle LHG$
$\Rightarrow \angle LHO=\angle LHG+\angle GHO=\angle OHB+\angle GHO=\angle GHB=90^o$
Mặt khác, $\angle LHG=\angle LCD=\angle LOM=\angle LOG \Rightarrow LHOG:tgnt$
$\Rightarrow \angle LGO=180^o-\angle LHO=90^o \Rightarrow LG \perp AO \Rightarrow LG \parallel AC$.
Mà $L$ là trung điểm $OC$ nên $G$ là trung điểm $AO$: cố định. Vậy ta có đpcm.

[Zaraki]

ĐỀ THI CHUYÊN TOÁN LAM SƠN 2012-2013

Môn: Toán

Ngày: 18 tháng 6 năm 2012

Thời gian thi: 150 phút (không kể thời gian giao đề)

Câu 1: (2.0 điểm) Cho $a = x + \frac{1}{x};b = y + \frac{1}{y};c = xy + \frac{1}{{xy}}$, với các số thực $x,y$ thỏa mãn $xy \ne 0$.
Tính giá trị biểu thức $A = {a^2} + {b^2} + {c^2} - abc$
Câu 2: (2.0 điểm)
Cho phương trình $(x - 1)(x - 2)(x - 3)(x - 6) = m{x^2}$ ($m là tham số).
Giả sử $m$ nhận các giá trị sao cho phương trình có 4 nghiệm ${x_1},{x_2},{x_3},{x_4}$ đều khác $0$.
Chứng minh rằng biểu thức \[\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \frac{1}{{{x_3}}} + \frac{1}{{{x_4}}}\] không phụ thuộc $m$.
Câu 3: (2.0 điểm)
Tìm số nguyên dương $n$ sao cho \[\frac{{n(2n - 1)}}{{26}}\] là số chính phương.
Câu 4: (3.0 điểm)
1) Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Gọi $(I), (K)$ lần lượt là các đường tròn nội tiếp tam giác $ABH, ACH$. Đường thẳng $KI$ cắt cạnh $AB$ tại $M$ và cạnh $AC$ tại $N$.
a) Chứng minh \[\frac{{HI}}{{HK}} = \frac{{HB}}{{HA}}\]
b) Chứng minh rằng $AM = AN$.
2) Cho tam giác nhọn $ABC$, $D$ là điểm trên cạnh $AB \; (D \ne A,B)$, trung tuyến $AM$ cắt $CD$ tại $E$. Chứng minh rằng nếu $\angle DBM + \angle DEM = {180^ \circ }$ thì $BC < AC\sqrt 2 $.

Câu 5: (1.0 điểm)
Cho $x,y$ là các số thực thay đổi thỏa mãn:
$$\left\{ \begin{array}{l} x > 1,y > 1 \\ x + y \le 4 \\ \end{array} \right.$$
Tìm giá trị nhỏ nhất của biểu thức: \[P = \frac{{{x^4}}}{{{{(y - 1)}^3}}} + \frac{{{y^4}}}{{{{(x - 1)}^3}}}.\]

Bài viết đã được chỉnh sửa nội dung bởi Phạm Quang Toàn: 19-06-2012 - 09:37

[ninhxa]

Câu 3
Tìm số nguyên dương $n$ sao cho $\frac{{n(2n - 1)}}{{26}}$ là số chính phương.

-Đặt $n(2n-1)=26q^2$ (1)
-Do VP chẵn và$2n-1$ lẻ nên $n$ chẵn hay $n=2k$
-Do đó
$(1)\Rightarrow k(4k-1)=13q^2$ (2)
-Nhận thấy: $(k,4k-1)=1$ nên
$(2)\Rightarrow \left\{\begin{matrix}k=u^2 \\ 4k-1=13v^2 \end{matrix}\right.\vee \left\{\begin{matrix}k=13u^2 \\ 4k-1=v^2 \end{matrix}\right.$
-Xét TH1 ta có
$\left\{\begin{matrix}k=u^2 \\ 4k-1=13v^2 \end{matrix}\right.\Rightarrow 4k=13v^2+1=12v^2+v^2+1$
$\Rightarrow v^2+1\vdots 4\Rightarrow v^2\equiv 3(mod4)$ (vô lý)
-Xét TH2 ta có:
$\left\{\begin{matrix}k=13u^2 \\ 4k-1=v^2 \end{matrix}\right.\Rightarrow 4k=v^2+1$
Tg tự ta cũng thấy vô lý
Vậy ko tồn tại $n$ thỏa mãn yêu cầu đề bài

Câu 1: (2.0 điểm) Cho $a = x + \frac{1}{x};b = y + \frac{1}{y};c = xy + \frac{1}{{xy}}$, với các số thực $x,y$ thỏa mãn $xy \ne 0$.
Tính giá trị biểu thức $A = {a^2} + {b^2} + {c^2} - abc$

-Làm theo kiểu cần cù bù thông minh vậy
-Ta có
$a^2+b^2+c^2=(x+\frac{1}{x})^2+(y+\frac{1}{y})^2+(xy+\frac{1}{xy})^2$
$=x^2+\frac{1}{x^2}+y^2+\frac{1}{y^2}+x^2y^2+\frac{1}{x^2y^2}+6$
-Lại có
$abc=\left ( x+\frac{1}{x} \right )\left ( y+\frac{1}{y} \right )\left ( xy+\frac{1}{xy} \right )=x^2y^2+x^2+\frac{1}{y^2}+y^2+\frac{1}{x^2}+\frac{1}{x^2y^2}+2$

-Do vậy A=4

Câu 5: (1.0 điểm)
Cho $x,y$ là các số thực thay đổi thỏa mãn:
$$\left\{ \begin{array}{l} x > 1,y > 1 \\ x + y \le 4 \\ \end{array} \right.$$
Tìm giá trị nhỏ nhất của biểu thức: $P = \frac{{{x^4}}}{{{{(y - 1)}^3}}} + \frac{{{y^4}}}{{{{(x - 1)}^3}}}$

-Áp dụng bdt AM_GM cho 4 số dương ta có:

$\frac{x^4}{(y-1)^3}+16(y-1)+16(y-1)+16(y-1)\geq 32x$
-Xây dựng bdt tg tự rồi cộng vế với vế ta dc:

$P\geq -16(x+y)+96\geq -16.4+96=32$

-Dấu bằng khi $x=y=2$

Câu 2: (2.0 điểm)
Cho phương trình $(x - 1)(x - 2)(x - 3)(x - 6) = m{x^2}$ (*) ($m$ là tham số).
Giả sử $m$ nhận các giá trị sao cho phương trình có 4 nghiệm ${x_1},{x_2},{x_3},{x_4}$ đều khác $0$.
Chứng minh rằng biểu thức $\frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} + \frac{1}{{{x_3}}} + \frac{1}{{{x_4}}}$ không phụ thuộc $m$
-Ta có:
$(*)\Leftrightarrow \left [ \left ( x-1 \right )\left ( x-6 \right ) \right ]\left [ (x-2)(x-3) \right ]=mx^2$
$\Leftrightarrow (x^2-7x+6)(x^2-5x+6)=mx^2$
$\Leftrightarrow \left ( x+\frac{6}{x}-7 \right )\left ( x+\frac{6}{x}-5 \right )=m$ (**)
-Đặt $x+\frac{6}{x}=t$
$(**)\Leftrightarrow (t-7)(t-5)=m\Leftrightarrow t^2-12t+35-m=0$ (1)
-Phương trình (*) có 4 nghiệm phân biệt nên phương trình (1) có 2 nghiệm t1, t2 phân biệt.
Theo hệ thức Vi-et ta có:
$\left\{\begin{matrix}t_1+t_2=12 \\t_1t_2=35-m \end{matrix}\right.$
-Do pt(*) có 2 nghiệm t1 và t2 phân biệt nên (*) tương đương với 2 pt:
$\left\{\begin{matrix}x+\frac{6}{x}=t_1 \\x+\frac{6}{x}=t_2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x^2-t_1x+6=0 (a)\\ x^2-t_2x+6=0 (b)\end{matrix}\right.$
-Giả sử $x_1,x_2$ là nghiệm pt (a) và $x_3,x_4$ là nghiệm pt (b)
-Theo hệ thức Vi-ét có
$\left\{\begin{matrix}x_1+x_2=t_1 \\ x_1x_2=6 \end{matrix}\right.$
$\left\{\begin{matrix}x_3+x_4=t_2 \\ x_3x_4=6 \end{matrix}\right.$
-Do đó:
$\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}+\frac{1}{x_4}=\frac{x_1+x_2}{x_1x_2}+\frac{x_3+x_4}{x_3x_4}=\frac{t_1+t_2}{6}=\frac{12}{6}=2$
-Ta có đpcm

Câu 4: (3.0 điểm)
1) Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Gọi $(I), (K)$ lần lượt là các đường tròn nội tiếp tam giác $ABH, ACH$. Đường thẳng $KI$ cắt cạnh $AB$ tại $M$ và cạnh $AC$ tại $N$.
a) Chứng minh $\frac{{HI}}{{HK}} = \frac{{HB}}{{HA}}$
b) Chứng minh rằng $AM = AN$



a)
-Ta có:
$\widehat{ABH}=\widehat{HAC}$ (cùng phụ $\widehat{BAH}$)
$\Rightarrow \widehat{IBH}=\widehat{KAH}$
-Lại có: $\widehat{IHB}=\widehat{KAH}(=45^0)$
$\Rightarrow \Delta IHB\sim \Delta KHA (g.g)$
$\Rightarrow \frac{HI}{HK}=\frac{HB}{HA}$
b)
-Ta có:
$\Delta AHB\sim \Delta CAB(g-g)$
$\Rightarrow \frac{HA}{HB}=\frac{CA}{AB}$
-Kết hợp với phần a ta có:
$\Rightarrow \frac{HI}{HK}=\frac{CA}{AB}$
$\Rightarrow \Delta IHK\sim \Delta BAC(c.g.c)$
$\Rightarrow \widehat{KIH}=\widehat{MBH}$
$\Rightarrow$ tứ giác IMBH nội tiếp
$\Rightarrow \widehat{AMN}=\widehat{IHB}=45^0$
$\Rightarrow \Delta AMN$ vuông cần
$\Rightarrow AM=AN$

Câu 4: (3.0 điểm)
2) Cho tam giác nhọn $ABC$, $D$ là điểm trên cạnh $AB \; (D \ne A,B)$, trung tuyến $AM$ cắt $CD$ tại $E$. Chứng minh rằng nếu $\angle DBM + \angle DEM = {180^ \circ }$ thì $BC < AC\sqrt 2 $



-Kẻ tia Ex cắt AC tại I sao cho $\widehat{AEI}=\widehat{ACB}$ (vì tam giác ABC nhọn nên luôn dựng dc)
-Ta chứng minh đc các tứ giác DEMB ; EICM; ADEI nội tiếp
-Do đó $CM.CB=CE.CD=CI.CA< CA^2$
Hay $\frac{1}{2}BC^2< AC^2\Leftrightarrow BC^2<2AC^2$
-Vậy: $BC< AC\sqrt{2}$

Xong đề rồi.

Bài viết đã được chỉnh sửa nội dung bởi ninhxa: 26-06-2012 - 17:33

[Poseidont]

CÂu 5

Bài này đổi biến đuợc mà, em h đang mắc mọi ngưòi thông cảm nha
$ \sum \frac{a}{a^2+2b+3}\leq \frac{1}{2}\Leftrightarrow \sum \frac{a}{4a+b+1}\leq \frac{1}{2}\Rightarrow \sum \frac{4a}{4a+b+1}\leq 2\Rightarrow \sum \frac{b+1}{4a+b+1}\geq 1$
Đến đây $\sum \frac{b+1}{4a+b+1}\geq 1=\sum \frac{b}{4a+b+1}+\frac{1}{4a+b+1}$
Ta áp dụng Cauchy Scwharz và áp dụng cái $a^2+b^2+c^2=3$ là $\square$