Chủ đề này có 4 trả lời

[THYH]

 

Ngày 1

 

Câu 1: Tìm tất cả các cặp số nguyên dương ($a, b$) sao cho $\gcd(a, b)=1$, và $\frac{a}{b}=\overline{ba}$. (Ví dụ, nếu $a = 92$ và $b = 13$, thì $b / a = 13,92$)

Câu 2: Cho $n$ là một số tự nhiên và $w_1, w_2, ....., w_n$ là $n$ quả cân. Ta gọi một tập $\{w_1, w_2, ...., w_n \}$ là một bộ hoàn hảo nếu chúng ta có thể cân được mọi trọng lượng từ $1,2, ....., W$ với những quả cân $w_1, w_2, ......, w_n$, trong đó $W =\sum_{i=1}^nw_i$. Chứng minh rằng nếu ta bỏ đi quả cân nặng nhất trong Bộ hoàn hảo thì những quả cân còn lại vẫn tạo 1 Bộ hoàn hảo.

Câu 3: Cho $M$ là trung điểm cung nhỏ $BC$ của đường tròn ngoại tiếp tam giác $ABC$. Giả sử rằng đường cao vẽ từ $B $cắt đường tròn tại $N$. Hai đường thẳng qua tâm đường tròn ngoại tiếp $O$ của tam giác $ABC$ song song với $MB$ và $MC$, thứ tự cắt $AB$ và $AC$ tại $K$ và $L$. Chứng minh rằng $NK = NL$.

 

 

Ngày 2

 

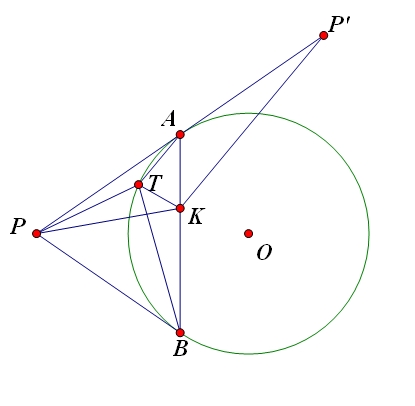
Câu 1: Cho $P$ là một điểm nằm ngoài đường tròn $C$.  $PA$ và $PB$ là tiếp tuyến với đường tròn $C$. Chọn một điểm $K$ trên $AB$. Giả sử rằng đường tròn ngoại tiếp tam giác $PBK$ cắt $C$ tại $T$. Gọi $P'$ là điểm đối xứng với $P$ qua $A$. Chứng minh rằng:

$$\angle PBT =\angle{P}'KA$$

Câu 2: Giả sử một bảng $ m\times n $. Ta viết một số nguyên vào mỗi ô trong bảng. Đến mỗi lượt, ta chọn một cột, một hàng, hoặc một đường chéo (đường chéo là tập hợp của các ô trong bảng mà hiệu giữa chỉ số hàng và chỉ số cột của chúng không đổi) và cộng hoặc $+1$ hoặc $-1$ vào tất cả các ô trong đó. Chứng minh rằng với mọi bảng $ 3\times 3 $ bất kì, ta có thể chuyển tất cả các số trong bảng về số 0, từ đó suy ra có thể chuyển mọi số trong bảng $m\times n $ về số $0$.

 

(Gợi ý:. Đầu tiên hãy nghĩ cách để chuyển các số trong bảng $3\times3$ về $0$)

Câu 3: Cho $\{a_n\}_{n=1}^{\infty}$ là một dãy số các số nguyên dương thỏa:

$$a_{n+2}=\left[\frac{2a_n}{a_{n+1}}\right]+\left[\frac{2a_{n+1}}{a_n}\right].$$

 

Chứng minh rằng có tồn tại một số nguyên dương $m$ thỏa $a_m=4$ và $a_{m +1}\in\{3,4 \}$.

Lưu ý. $[x]$ là số nguyên lớn nhất không vượt quá $x$.

 -----Hết------

 

 

Bài viết đã được chỉnh sửa nội dung bởi THYH: 19-07-2013 - 16:06

[BlackSelena]

Câu 3 ngày 1 phải là đường cao từ $A$ chứ nhỉ ?

[BlackSelena]

Câu 3: Cho $M$ là trung điểm của (nhỏ hơn) cung $BC$ trong đường tròn ngoại tiếp tam giác $ABC$. Giả sử rằng đường cao vẽ từ $B $cắt đường tròn tại $N$. Vẽ hai dây qua đường tròn $O$ của ABC song song với $MB$ và $MC$, mà cắt $AB$ và $AC$ tại $K$ và $L$, tương ứng. Chứng minh rằng $NK = NL$.

Chờ mãi ko thấy chủ topic đính chính nên liều giải vậy @@!
Dễ có $AKOL$ là tgnt. Dựng hình thang cân $KLOP$ thì hiển nhiên $P \in (AKOL)$

$\Rightarrow KP = OL \Rightarrow \angle KAP = \ angle OLA = \angle BAN$

$\Rightarrow P \in AN$
Mặt khác, do $AN \parallel IM$ nên $\angle OMN = 180^\circ - \angle ANM = \angle ACM = \angle ALO = \angle NPO$

$\Rightarrow POMN$ là hình bình hành.

$\Rightarrow NP = NO = OM$
Từ đây có $\triangle KON = \triangle LPN$. Tức $NK = NL$. Ta có đpcm!

p/s: Gg Trans quá lố r ==

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 09-07-2013 - 21:41

[THYH]

iranmo2013.png

Chờ mãi ko thấy chủ topic đính chính nên liều giải vậy @@!
Dễ có $AKOL$ là tgnt. Dựng hình thang cân $KLOP$ thì hiển nhiên $P \in (AKOL)$

$\Rightarrow KP = OL \Rightarrow \angle KAP = \ angle OLA = \angle BAN$

$\Rightarrow P \in AN$
Mặt khác, do $AN \parallel IM$ nên $\angle OMN = 180^\circ - \angle ANM = \angle ACM = \angle ALO = \angle NPO$

$\Rightarrow POMN$ là hình bình hành.

$\Rightarrow NP = NO = OM$
Từ đây có $\triangle KON = \triangle LPN$. Tức $NK = NL$. Ta có đpcm!

p/s: Gg Trans quá lố r ==

:v chờ mai mới sửa 

[gogo123]

Ngày 2.

Bài 1.(hình vẽ)

   Dễ thấy $\angle PBT=\angle TAB;\angle ATB=\angle KAP'$.

   Do đó để chứng minh kết quả bài toán cần chứng minh $\Delta ATB\sim \Delta KAP'(c.g.c)$.

Thật vậy do $\angle ATB=\angle KAP'$ nên chỉ cần chứng minh

$$\frac{AK}{AT} = \frac{AP'}{TB} = \frac{BP}{BT}$$

Mà tứ giác $KTPB$ nội tiếp nên $ \angle TPB = \angle AKT $ và $\angle TAK= \angle TBP$ nên hai tam giác $TPB$ và $TAK$.

Suy ra : $\frac{AK}{AT} = \frac{BP}{BT}$ (đpcm)

Bài 2. Chú ý ta có thể đồng thời tăng giá trị ở mỗi hàng (cột ,đchéo) lên một số nguyên k bất kì (k có thể âm).

Xét TH bảng $3*3$ ta có: Hàng 1,2,3 cộng thêm $H_1;H_2;H_3$, cột 1,2,3 cộng thêm $C_1;C_2;C_3$, đường chéo có hiệu -2,-1,0,1,2 cộng thêm $D_1,D_2,D_3,D_4,D_5$

Khi đó cần có  $M(i,j)=H_i+C_j+D_{i-j}$. Cho $M_i$ tăng thêm 1 đơn vị ta chỉ việc bién đổi phần $H,C,D$ cho phù hợp là thoã mãn bài toán,

Bài 3.  $a_{n+2}=\left [ \frac{2a_n}{a_{n+1}} \right ]+\left [ \frac{2a_{n+1}}{a_n} \right ] $

Dễ thấy trong hai số nghịch đảo có 1 sô không nhỏ hơn 1 nên $a_n \geq 2$ với mọi n.

Và nếu có $a_{n}=a_{n+1}$ thì $a_{n+2}=4$

 

 Nếu có 1 số $a_n=2$ thì $a_{n+2}=a_{n+1} + \left [ \frac{4}{a_{n+1}} \right ]$.

   Khi đó 

              TH1. $a_{n+1}=3 \Rightarrow a_{n+2}=4;a_{n+3}=3$,t/m

              TH2.$a_{n+1}=4 \Rightarrow a_{n+3}=3;a_{n+4}=4;a_{n+5}=3$,t/m

              TH3. $a_{n+1}>5$ thì $a_{n+2}=a_{n+1}$ $ \Rightarrow$  $a_{n+3}=4$,tiếp tục xử lí như TH $a_n \geq 3$

 

 Nếu  $a_n \geq 3$ với mọi n thì

      TH1. Tồn tại $a_n<a_{n+1}$ suy ra $\left [ \frac{2a_{n+1}}{a_n} \right ] \leq a_{n+1}-1$ và $\left [ \frac{2a_n}{a_{n+1}} \right ] <1 $. 

        Do đó $a_{n+2} \leq a_{n+1}$ nên dãy có số hạng $a_{n+1}$ là lớn nhất.

   Hay ta có nhân xét là nếu tồn tại $a_n<a_{n+1}$ thì mộ số hạng phía sau $a_{n+1}$ đều không lớn hơn  $a_{n+1}$ và dương nên tồn tại một dãy vô hạn số hạng liên tiếp bằng nhau ( cùng = 4), t/m

       TH2. $a_{n} \geq a_{n+1}$ với mọi $n$ thì tồn tại một dãy có vô số số hạng liên tiếp cùng bằng nhau và bằng 4,t/m.

Như vậy ta có đpcm

 

 

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi gogo123: 13-07-2013 - 01:17