Chủ đề này có 1 trả lời

[vutuanhien]

Cho tam giác đều $ABC$, $D$ là 1 điểm nằm trên cạnh $BC$ ($D$ không trùng với các đỉnh). Gọi $I$ là tâm đường tròn ngoại tiếp tam giác $ABD$ đối diện với cạnh $AB$, $J$ là tâm đường tròn bàng tiếp tam giác $ACD$ đối diện với cạnh $AC$. Giả sử $E$ là giao điểm thứ 2 của đường tròn ngoại tiếp các tam giác $ABI$ và tam giác $ACJ$. Chứng minh rằng:$A$ là tâm đường tròn nội tiếp tam giác $IEJ$

(Turkey JBMO TST 2013)

 

[gogo123]

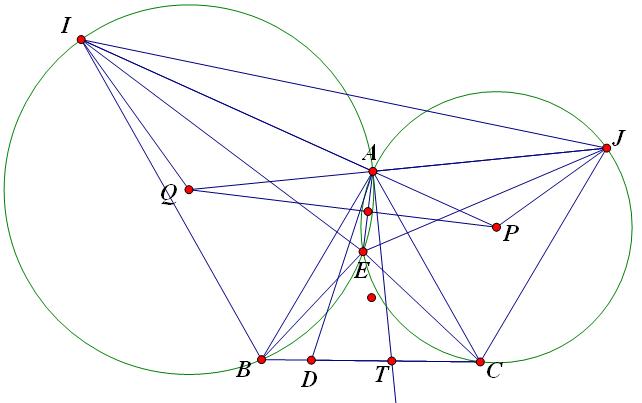
Gọi $Q,P$ lần lượt là tâm đường tròn ngoại tiếp $ABI,ACJ$.

Trước hết ta chứng minh $(Q,A,J);(P,A,I)$ là hai bộ điểm thẳng hàng.

   Gọi AT là phân giác $\angle CAD$, suy ra $AT\perp AJ$ (phân giác 2 góc bù nhau)

   Ta cần chứng minh $AT \perp AQ$ hay $AT$ là tiếp tuyến của $(Q)$, thật vậy ta có:

      $\angle AIB =180^{\circ}- \angle IAB -\angle IBA = 180^{\circ}-(90^{\circ}-\frac{ \angle SAD}{2} )-60^{\circ} = \frac{ \angle SAD}{2} + 30 ^{\circ}$

    $\angle BAT =60^{\circ}-\frac{ \angle CAD}{2}=\frac{ \angle SAD}{2} + 30 ^{\circ}$

  Do đó: $\angle AIB= \angle BAT $ hay $AT$ là tiếp tuyến của $(Q)$ suy ra $A,Q,J$ thẳng hàng.

  Tương tự ta cũng có $I,A,P$ thẳng hàng.

Trở lại bài toán ta sẽ chứng minh $JA$ là phân giác $\angle IJE$, thật vậy:

Ta có: $\angle ABI =\angle ACJ=60^{\circ} $ suy ra hai dây cung bị chắn $AI : AJ = R_{(Q)}:R_{(P)}$ hay  $\frac{AI}{AJ}=\frac{AQ}{AP}$

   Suy ra tứ giác $JIQP$ nội tiếp $\Rightarrow \angle IJA= \angle APQ$

   Xét đường tròn $(P)$ có $PQ$ vuông góc với dây $AE$ nên $\angle APQ =\angle AJE = 0,5.Sđ(\widehat{AE})$

  Suy ra : $\angle IJA= \angle APQ = \angle AJE$

Suy ra  $JA$ là phân giác $\angle IJE$

Tương tự $IA$ là phân giác $\angle JIE$

Vậy $A$ là tâm đường tròn nội tiếp tam giác $JIE$ (đpcm)

 

Hình gửi kèm

•