Thời gian: 180 phút.
Bài 1: (5 điểm)
Tìm tất cả các hàm số $f:\mathbb{R^*} \to \mathbb{R}$ sao cho $f(x + y) = {x^2}f\left( {\frac{1}{x}} \right) + {y^2}f\left( {\frac{1}{y}} \right),\forall x,y \in \mathbb{R^*}$
Bài 2: (5 điểm)
Cho $n$ số nguyên dương $x_1, x_2,...x_n$ đôi một khác nhau ($n \ge 2$). Đặt $A=\{1,2,...,n\}$. Với mội $i \in A$ lấy ${p_i} = \prod\limits_{j \in A\backslash \{ i\} } {({x_i} - {x_j})} $. Chứng minh $\sum\limits_{i \in A} {\frac{{{x_i}^k}}{{{p_i}}}} $ nguyên với mọi $k$ tự nhiên.
Bài 3: (5 điểm)
Cho đường thẳng $d$ và điểm A không nằm trên $d$. Gọi $H$ là hình chiếu của $A$ trên d và K là trung điểm của $AH$. Hai đường tròn $(M), (N)$ di động nhưng luôn tiếp xúc với d và tiếp xúc với nhau tại A. Chứng minh:
a) Phương tích của K với đường tròn đường kính $MN$ không đổi.
b) Chứng minh đường tròn đường kính $MN$ luôn tiếp xúc với đường tròn cố định.
Bài 4: (5 điểm)
Cho bảng kẻ ô vuông kích thước $(2n) \times (2n+1)$. Hãy tìm giá trị lớn nhất của $k$ sao cho $k$ thoả mãn điều kiện: ta có thể tô màu $k$ ô vuông đơn vị của bảng sao cho không có hai ô vuông đơn vị nào được tô mà có đỉnh chung.
Ngày 2
Thời gian: 180 phút.
Bài 5: (6 điểm)
Cho số nguyên tố $p>3$. Gọi $k = \left\lfloor {\frac{{2p}}{3}} \right\rfloor $. Chứng minh:
\[\sum\limits_{i = 1}^k {C_p^i} \vdots {p^2}\]
Bài 6: (7 điểm)
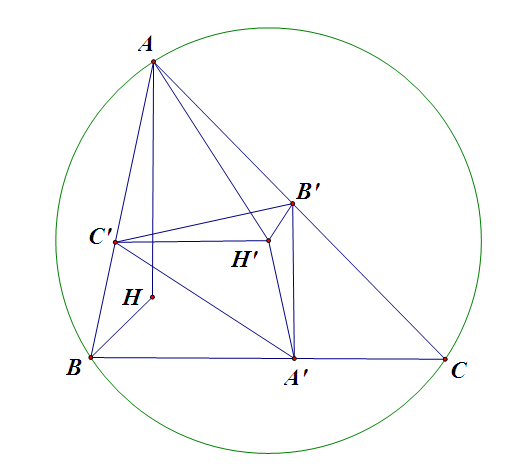
Cho tam giác $ABC$ và điểm $C'$ nằm trên đường thẳng $AB$. Chứng minh rằng:
a) Tồn tại duy nhất tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ mà các điểm $A'$ và $B'$ nằm lần lượt trên đường thẳng $BC$ và $AC$.
b) Trực tâm của tam giác $A'B'C'$ không phụ thuộc vị trí của điểm $C'$ trên đường thẳng $AB$.
Bài 7: (7 điểm)
Cho $(H)$ là một đa giác đều $24$ cạnh. Mỗi đỉnh của $(H)$ sẽ được tô bởi chỉ một trong hai màu xanh và đỏ. Khi đó, nếu $(K)$ là một đa giác đều thoả mãn đồng thời hai điều kiện:
- Tập đỉnh của $(K)$ là tập con của tập đỉnh của $(H)$.
- Tất cả các đỉnh của $(K)$ được tô bởi cùng một màu.
thì ta gọi $(K)$ là một mẫu đơn sắc. Hãy tính số cách tô màu các đỉnh của $(H)$ sao cho không có mẫu đơn sắc nào được tạo ra.
Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-09-2013 - 14:27