Đề chọn đội tuyển HSG Lâm Đồng 2013 – 2014
Bài 1: Giải hệ phương trình
$$\left\{ \begin{matrix} 8{{x}^{3}}+2y=\sqrt{y+5x+2} \\ \left( 3x+\sqrt{1+9{{x}^{2}}} \right)\left( y+\sqrt{1+{{y}^{2}}} \right)=1 \\ \end{matrix} \right.$$ .
Bài 2: Cho $a,b,c$ là 3 số thực dương thỏa $abc=1$ . Tìm giá trị nhỏ nhất của biểu thức
$$P=\frac{bc}{{{a}^{2}}b+{{a}^{2}}c}+\frac{ca}{{{b}^{2}}c+{{b}^{2}}a}+\frac{ab}{{{c}^{2}}a+{{c}^{2}}b}$$
Bài 3:
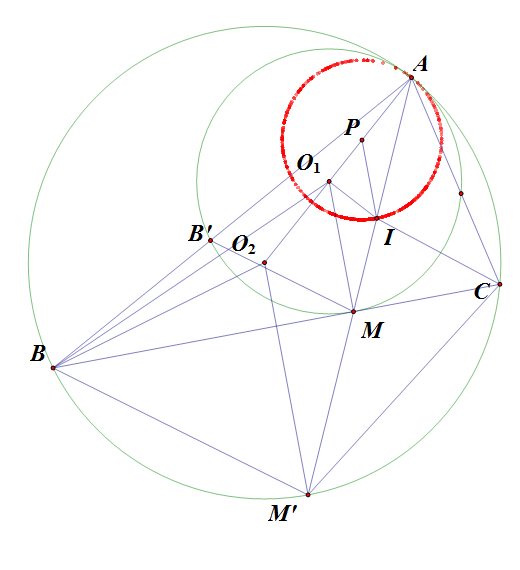
1) Cho hai đường tròn $\left( {{O}_{1}} \right)$ và $\left( {{O}_{2}} \right)$ lần lượt có bán kính là ${{R}_{1}},{{R}_{2}}\left( {{R}_{1}}<{{R}_{2}} \right)$ tiếp xúc trong tại $A$. Gọi $M$ là điểm di động trên $\left( {{O}_{1}} \right)$ ($M$ khác $A$), tiếp tuyến của $\left( {{O}_{1}} \right)$ tại $M$ cắt $\left( {{O}_{2}} \right)$ tại $B$ và $C$. Gọi $M'$ ($M'$ khác $A$) là giao điểm của $AM$ với $\left( {{O}_{2}} \right)$.
a) Chứng minh $AM’$ là đường phân giác của góc $\widehat{ABC}$ .
b) Tìm quỹ tích tâm $I$ của đường tròn nội tiếp tam giác $ABC$.
2) Cho đường tròn $\left( C \right)$ có tâm $I$ và đường kính $AB$, trên đoạn $IB$ lấy điểm $C$ ($C$ khác $I$ và $B$). Đường thẳng $(d)$ vuông góc với $AB$ tại $C$ và $H$ là điểm thay đổi trên $(d)$. Đường thẳng $AH$ cắt đường tròn $\left( C\right)$ tại điểm $D$ và đường tròn $BH$ cắt đường tròn $\left( C\right)$ tại $E$. Chứng minh đường thẳng $DE$ luôn đi qua điểm cố định.
Bài 4: Cho dãy số $\left( {{x}_{n}} \right),n=1,2,3,...$ xác định bởi
$$\left\{ \begin{matrix} {{x}_{1}}=1 \\ {{x}_{n+1}}=\sqrt{{{x}_{n}}\left( {{x}_{n}}+1 \right)\left( {{x}_{n}}+2 \right)\left( {{x}_{n}}+3 \right)+1}\end{matrix} \right.,n=1,2,3,...$$
a) Chứng minh : $\underset{n\to +\infty }{\mathop{\lim }}\,{{x}_{n}}=+\infty $
b) Tìm $\underset{n\to +\infty }{\mathop{\lim }}\,\sum\limits_{k=1}^{n}{\frac{1}{{{x}_{k}}+2}}$
Bài 5: Tìm tất cả hàm số liên tục $f:\mathbb{R}\to \mathbb{R}$ sao cho
$$f\left( x \right)+f\left( {{x}^{4}} \right)=4026+x+{{x}^{4}}$$ .