ĐỀ THI CHỌN ĐỘI TUYỂN HỌC SINH GIỎI LỚP 12 TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
BÌNH ĐỊNH- NĂM 2013-2014
________________________________
Bài 1: Cho dãy số $(U_n)$ được xác định bởi: $U_0=U_1=1, U_{n+2}=\sqrt[3]{U_{n+1}}+\sqrt[3]{U_n},\forall n\in \mathbb{N}$
Chứng minh rằng dãy $(U_n)$ có giới hạn hữu hạn. Tìm giới hạn đó.
Bài 2: Cho ba số thực $a,b,c$ biến thiên trong đoạn $[1;2]$ và thỏa mãn: $a+b+c=4$
Tìm giá trị lớn nhất của biểu thức:$$P=\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}$$
Bài 3: Có bao nhiêu bộ sắp thứ tự $(a,b,c)$, với $a,b,c$ là các số nguyên dương thỏa mãn: $[a,b,c]=2^3.3^5.5^7.7^{11}$ ? (Kí hiệu $[a,b,c]$ là bội chung nhỏ nhất của ba số $a,b,c$ nguyên dương)
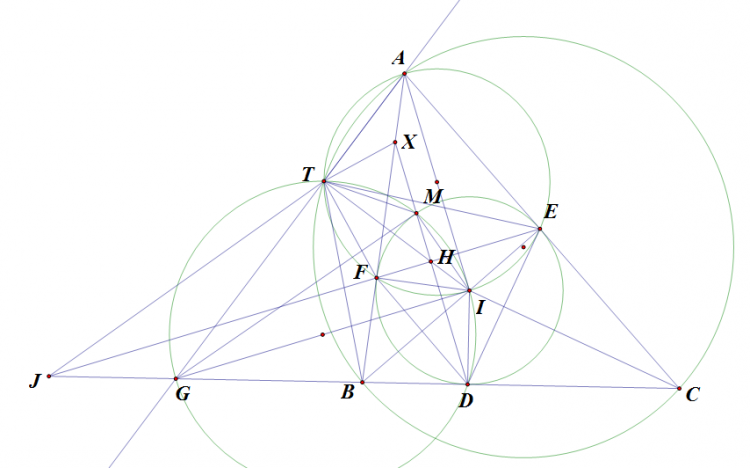
Bài 4: Đường tròn nội tiếp $\Delta ABC (AB\ne AC)$, tiếp xúc với cạnh $BC,CA,AB$ tương ứng tại $D,E,F$. Đường thẳng qua $D$ và vuông góc với $FE$ cắt cạnh $AB$ tại $X$, giao điểm thứ hai của đường tròn ngoại tiếp tam giác $AEF$ và $ABC$ là $T$. Chứng minh rằng: $TX\perp TF$
Bài viết đã được chỉnh sửa nội dung bởi thanhdotk14: 02-10-2013 - 19:03