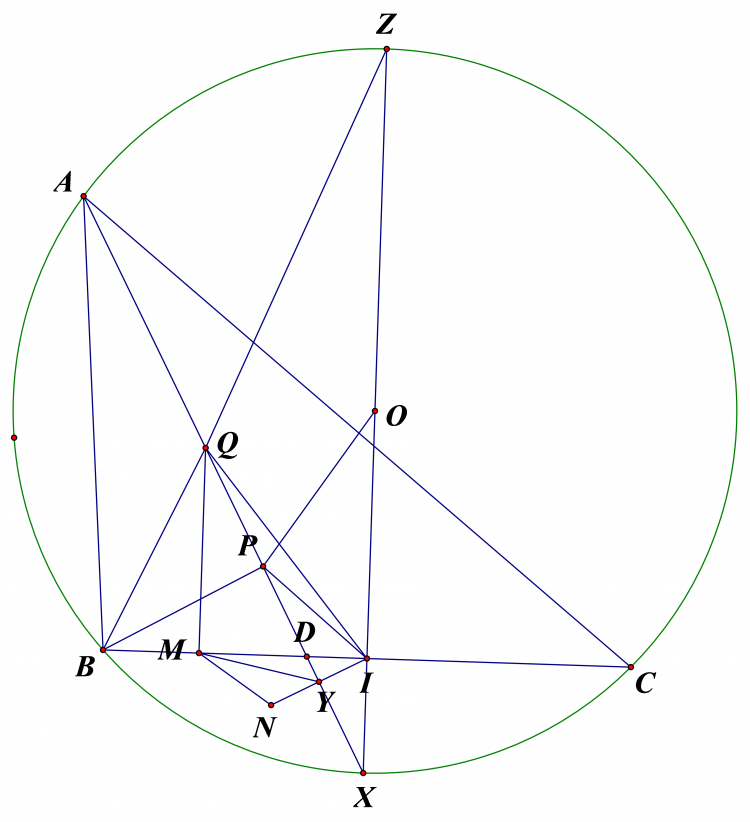
Cho tam giác $ABC$ nội tiếp $(O)$, $I$ là trung điểm cạnh $BC$. Phân giác trong $AD$ ($D$ trên cạnh $BC$),hai điểm $P,Q$ trên cạnh $AD$ thoả mãn $\angle CBP=\angle ABQ$. $M$ là hình chiếu của $Q$ trên $BC$, $N$ đối xứng với $I$ qua $AD$. Chứng minh $MN \perp OP$
Bài viết đã được chỉnh sửa nội dung bởi NVHT: 24-12-2013 - 23:01