Năm 1899, David Hilbert công bố tác phẩm Cơ sơ Hình học (CSHH), trong đó đã nêu lên một hệ tiên đề cho hình học Euclid, sau nay được gọi là Hệ tiên đề Hilbert (HTĐH).
HTĐH từng được coi là một hệ tiên đề hoàn hảo của Hình học Euclid, vì nó thỏa mãn 3 điều kiện khắt khe của một hệ tiên đề do chính Hilbert nêu lên: độc lập, đầy đủ, phi mâu thuẫn. Đến nay công trình này đã được coi là một vấn đề cổ điển thuộc cơ sở hình học, chẳng có gì đáng bàn thêm. Tuy nhiên, sau khi xem xét kỹ cuốn CSHH và một số tài liệu liên quan, tôi xin mạnh dạn nêu lên một số nghi vấn về tính hoàn hảo của HTĐH.
Để tránh hiểu lầm, xin nhấn mạnh rằng mọi chi tiết trong bài này chỉ đề cập đến HTĐH mà thôi, không liên quan đến bất cứ hệ tiên đè hình học nào của ai khác, nếu có.
1. HTĐH có bao nhiêu tiên đề?
Tài liệu đầu tiên tôi được đọc về HTĐH là cuốn Bách khoa toán học trẻ của Liên Xô, trong đó nói ìhình học có khoảng 19 tiên đề” (1). Chữ ìkhoảng” (nguyên văn tiếng Nga là okolo) làm tôi nghi ngờ tính chính xác của thông tin, thậm chí nghĩ rằng tác giả cuốn bách khoa này không nắm vững HTĐH.
Năm 1996, GS Văn Như Cương tuyên bố: ìPhải chờ đến cuối thế kỷ XIX nhà toán học Hilbert mới đề nghị một hệ tiên đề đầy đủ cho Hình học Euclid bao gồm 19 tiên đề…”, nhưng không cho biết thông tin đó dựa vào tài liệu nào. Phải chăng cũng dựa theo Bách khoa toán học trẻ của Liên Xô? Nếu đúng như thế thì số liệu này không đáng tin cậy.
Vài năm sau, sau khi tham khảo thêm nhiều tài liệu mới, tôi hết sức ngạc nhiên thấy số tiên đề trong các tài liệu đó mâu thuẫn với nhau (xem bảng dưới)
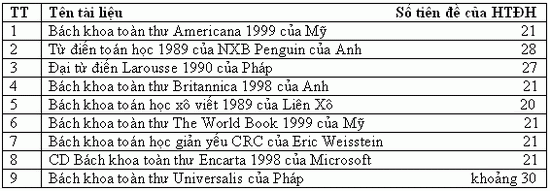
Xin chú ý tài liệu 9 – Bách khoa toàn thư Universalis – cũng chỉ cung cấp một con số gần đúng ìkhoảng 30 tiên đề” (une trentaine d’axiomes), thay vì một số tiên đề xác định.
Sự mâu thuẫn giữa các tài liệu đã thúc đẩy tôi viết thư phỏng vấn một số nhà toán học, và họ đã trả lời.
Giáo sư toán học Edmund Robertson ở Đại học Saint Andrews ở Anh tỏ ra ngạc nhiên và nói: ìTôi luôn luôn nghĩ rằng Hilbert nêu lên 21 tiên đề. Tôi hoàn toàn không biết tại sao những nguồn tại liệu khác mà ông trích dẫn lại đưa ra những số liệu khác”.
Giáo sư toán học John O’Connor cũng tại Đại học St Andrews đã trả lời bằng cách cung cấp một địa chi Internet về đề tài này: http://mathworld.wol...ertsAxioms.html. Tôi vào địa chỉ đó và thấy ngay rằng không có gì mới. Đó là trang web của tài liệu 7 đã thống kê ở trên. Tuy nhiên, tài liệu này nói rõ nguồn tư liệu tham khảo, đó là cuốn CSHH của Hilbert bằng tiếng Anh, do Open Court tái bản lần thứ hai tại Chicago năm 1980, xin viết tắt là CSHH 1980. Như vậy theo CSHH 1980, HTĐH có 21 tiên đề.
Sau khi đọc bài Một thế kỷ tranh cãi về nền tảng của toán học trên Internet, một bài giảng hấp dẫn của Gregory Chaitin, giáo sư toán học thuộc Viện Thomas Watson của IBM, trong đó đề cập khá sâu sắc đến chương trình tiên đề hóa của Hilbert, tôi nghĩ chắc chắn tác giả phải nắm vững HTĐH. Tôi liên lạc và nhận được trả lời” ìTôi e rằng tôi không trả lời được các câu hỏi lý thú của ông về các hệ tiên đề của Hilbert, vì hình học không thuộc lĩnh vực của tôi”. Bù lại, giáo sư cung cấp một thông tin liên quan đến tính đầy đủ của hình học sơ cấp, sẽ được trình bày ở phần II.
Tóm lại đến lúc đó, số tiên đề của HTĐH vẫn còn là một ẩn số..
Nhưng rồi ìcái gì sẽ xảy ra, phải xảy ra”, ìQue sera, sera”. Đầu năm 2000 tôi đã tìm mua được một cuốn CSHH mới tinh, nhan đề Foundations of Geometry, tác giả David Hilbert, tái bản bằng tiếng Anh lần thứ hai, do Open Court, La Salle xuất bản năm 1971 tại Illinois, Mỹ, in lại năm 1999, xin viết tắt là CSHH 1971.
Ngay tại chương I, mục 1, sau phần định nghĩa các khái niệm, Hilbert viết:
Các tiên đề của hình học có thể được chia thành năm nhóm. Mỗi nhóm thể hiện những yếu tố xác định dựa trên trực giác của chúng ta. Các nhóm tiên đề này sẽ được đặt tên như sau:
Nhóm I-Các tiên đề về sự khu trú (Axioms of Incidence), gồm 8 tiên đề.
Nhóm II- Các tiên đề về thứ tự (Axioms of Order), gồm 4 tiên đề.
Nhóm III-Các tiên đề về sự bằng nhau (Axioms of Congruence), gồm 5 tiên đề.
Nhóm IV-Tiên đề đường song song (Axioms of Parallels), gồm một tiên đề.
Nhóm V-Các tiên đề về tính liên tục (Axioms of Continuity), gồm 2 tiên đề.
Như vậy, theo CSHH 1971, HTĐH có 20 tiên đề!
Đến đây, xin độc giả thử cùng với tôi làm một phân tích so sánh số liệu.
2. Phân tích so sánh
Trước hết xin độc giả đọc kỹ một đoạn trích trong Lời tựa của CSHH 1971: ìKể từ lần xuất bản đầu tiên trở đi, cuốn Cơ sở Hình học của Hilbert bản thân nó đã trải qua những thay đổi lớn (major changes) đến nỗi cuốn xuất bản lần cuối cùng khó mà nhận ra cuốn xuất bản đầu tiên. Vì lý do đó, điều rất quan trọng đối với một học sinh nghiêm túc và giáo viên trung học là nên sử dụng cuốn xuất bản lần cuối cùng này”. Đó là ý kiến của Harry Goheen, giáo sư toán học tại Đại học Oregon ở Mỹ. Goheen viết tiếp: ìNhiều nhà toán học đã phát biểu ý kiến rằng công trình của Hilbert là một công trình sơ cấp (elementary) hoặc ít quan trọng (of small importance), đầy rẫy sai sót (full of error), và không có ý nghĩa hiện đại (devoid of modern significance). Với sự kính trọng đối với tất cả những ai có những chỉ trích đó, tôi xin đặc biệt nhấn mạnh tầm quan trọng to lớn của ý định xây dựng một hệ tiên đề đầy đủ phi mâu thuẫn của hình học và một sự tổng hợp của các tiên đề này bên trong giải tích và số thực”.
Tự ý kiến trên, kếthợp với những bằng chứng rõ ràng khác, có thể tin rằng Hilbert đã nhiều lần thay đổi hệ tiên đề của ông, và đó là những thay đổi chủ yếu.
Thật vậy, có thể thấy rõ sự thay đổi này ngay trong CSHH 1971: Ghi chú ở trang 6 nói rằng Định lý 5 trong lần xuất bản đầu tiên vốn được coi là một tiên đề, nhưng năm 1902, E.H.Moore đã chứng minh đó là hệ quả của các tiên đề nhóm I và II. Ghi chú ở trang 27 cho biết Định lý 32 trong những lần xuất bản trước đây vốn được coi là một tiên đề về tính đầy đủ. Vậy có thể biết chắc chắn rằng số tiên đề trong lần xuất bản đầu tiên (1899) ít nhất phải là: 20 + 2 = 22. Năm 1902, một tiên đề thành Định lý 5, vậy số tiên đề là 22 – 1 = 21. Đến khi Tiên đề về sự đầy đủ biết thành Định lý 32 thì số tiên đề còn lại là 21 – 1 = 20. Nhưng nếu chú ý đến ý kiến của Goheen thì sự thay đổi chắc chắn đã xảy ra nhiều hơn như thế. Nghĩa là không phải chỉ có hai lần thay đổi, và số tiên đề ban đầu không phải là 22, mà lớn hơn nhiều.
Đến đây, tôi mạnh dạn phỏng đoán rằng số tiên đề ban đầu là ìkhoảng 30”, đúng như Bách khoa Universalis của Pháp (tài liệu 9) đã nói. Sau đó số tiên đề được giảm dần, xuống 28 (tài liệu 2), rồi 27 (tài liệu 3), rồi 21 (tài liệu 1, 4, 6, 7, 8 và CSHH 1980) và 20 (tài liệu 5 và CSHH 1971) như những con số trong bảng thống kê ở trên. Sự phỏng đoán này có thể kiểm tra đúng hay sai nếu có điều kiện tiếp xúc với tất cả các nhà xuất bản của các tài liệu nói trên. Nhưng điều đó đòi hỏi thì giờ và công sức, tôi chưa thể làm được.
Chú ý rằng chính Hilbert đã thể hiện rõ mong muốn tìm một hệ tiên đề với số tiên đề càng ít càng tốt. Ông viết trong phần dẫn nhập: ìCông trình nghiên cứu hiện tại này là một cố gắng mới để lập cho hình học một tập hợp các tiên đề đầy đủ, và càng đơn giản càng tốt và để từ đó rút ra những định lý hình học quan trọng nhất …”. Mặt khác, có thể tin rằng không có một thiên tài nào ngay lúc đầu có thể định ra một số tiên đề chính xác được, vì quá trình xây dựng tiên đề , như chính Hilbert nói, phải bắt đầu từ trực giác. Tất nhiên sau đó phải chứng minh. Nhưng dù là thiên tài, không có gì để đảm bảo rằng chứng minh hôm nay tưởng là đúng sẽ vĩnh viễn đúng.



3. Nghi vấn tính hoàn hảo của HTĐH
i) Về tính độc lập: Hai tiên đề được coi là độc lập với nhau nếu tiên đề này không phải là hệ quả của tiên đề kia và ngược lại. Vậy mỗi lần một tiên đề bị phát hiện không phải là tiên đề mà là một định lý thì có nghĩa là chứng minh trước đó về tính độc lập của hệ tiên đề là sai. Nếu sự phỏng đoán số tiên đề ban đầu là ìkhoảng 30” và cuối cùng là 20 là đúng, thì suy ra Hilbert đã sai lầm ìkhoảng 10” lần trong việc chứng minh tính độc lập của hệ tiên đề (!). Nhận xét này có thể không làm đẹp lòng những người vốn quen thần thánh hóa Hilbert, nhưng lại phù hợp với ý kiến của những người chỉ trích Hilbert mà Goheen đã nói trong Lời tựa của CSHH 1971 như ở trên đã dẫn, rằng công trình của Hilbert ìđầy rẫy sai sót”. Vì thế tôi ngờ vực độ tin cậy của kết quả hiện tại, và xin mạnh dạn nêu lên một nghi vấn: Có gì để bảo đảm rằng số tiên đề cuối cùng là 20?
ii) Về tính phi mẫu thuẫn: Bách khoa toán học Xô viết 1989 viết: ìHệ tiên đề Hilbert là phi mâu thuẫn nếu số học phi mâu thuẫn”. Số học có phi mâu thuẫn hay không? Định lý bất toàn của Kurt Godel đã chứng minh rằng không thể chứng minh được tính phi mẫu thuẫn của số học. Vậy suy ra tính phi mâu thuẫn của Hệ tiên đề Hilbert cũng chỉ có giá trị tương đối mà thôi.
iii) Về tính đầy đủ: Tính đầy đủ là điểm hơn hẳn của HTĐH so với Euclid. Nhưng làm thể nào để chứng minh tính đầy đủ của HTĐH? Trong cuốn CSHH 1971 không có phần nào trình bày tính đầy đủ (điều này làm tôi ngạc nhiên). Gregory Chaitin trả lời phỏng vấn của tôi, nói: ìKhoảng 1940, Alfred Tarski, một nhà toán học Ba Lan, khám phá ra một quy trình có thể chứng minh tính đầy đủ của hình học Euclid. Thông qua đại số Descartes và sử dụng Lý thuyết các trường số thực đóng, quy trình Tarski cho phép chứng minh hoặc phủ định bất kỳ một định lý nào của hình học Euclid trình bày dưới dạng hình thức. Công trình của Tarski có tên là Tính đầy đủ của đại số và hình học sơ cấp hiện chỉ có bằng tiếng Pháp do Armand Colline xuất bản tại Paris năm 1974. Về sau người ta cho chạy thử quy trình Tarski trên computer nhưng cực kỳ chậm. Tôi nhớ không rõ lắm rằng quy trình này hình như dựa trên thủ tục Sturm để tìm nghiệm của các phương trình đại số. Nhưng đáng tiếc là công trình này không nhận được sự chú ý cần thiết”. Tuy nhiên Chaitin không nói gì về mối liên hệ giữa công trình của Tarski với HTĐH. Giuseppe Longo, giáo sư toán học tại Ecole Normale Supérieure, nói: ìCó một truyền thống mạnh mẽ của của những người đi theo chủ nghĩa toán học hình thức (chủ nghĩa Hilbert) trong thế kỷ này (20) đi theo hướng viết lại lịch sử và và trình bày nó như một cuộc trường chinh tới việc thiết lập hệ tiên đề như ngày nay. Trong công trình của Hilbert không có một cấu trúc nào định trước làm chỗ dựa để người ta kiểm chứng tính đầy đủ (giống như số học của Peano và cấu trúc đại số), do đó tính đầy đủ có thể chỉ là một đặc thù mang tính lý thuyết”.
4. Kết
Qua những phân tích trên, tôi thấy cần phải nghi vấn mức độ hoàn hảo của HTĐH mà nhiều tài liệu, sách báo và một số nhà toán học vẫn thường quảng cáo rùm beng. Cần có những nghiên cứu toán học sâu sắc hơn để trả lại cho Hệ tiên đề Hilbert giá trị đúng với thực chất của nó, tránh bệnh sùng bái thiếu căn cứ.
PHẠM VIỆT HƯNG (Tạp chí Tia sáng, tháng 8. 2002)







