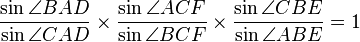Lời giải của toán thủ $\boxed{MSS_{04}}$ : Nguyễn Trung Hiếu
Trước tiên ta chứng minh bổ đề sau:
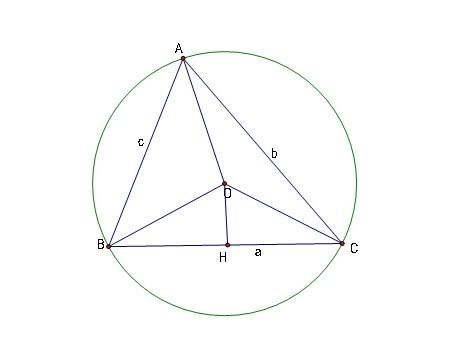
Bổ Đề $\boxed{1}$: Cho tam giác $ABC$ nhọn. Chứng minh rằng $S_{ABC}=\dfrac{1}{2}.AB.AC.sin \angle BAC$
$\triangleright$Chứng minh :

Kẻ đường cao $BH$ của tam giác $ABC$ ta có :
Ta có : $S_{ABC}=\dfrac{1}{2}.AC.BH=\dfrac{1}{2}.AC.AB.sin \angle BAC$ (đpcm)
Bổ đề $\boxed{2}$ : Định lý $\boxed{Cêva}$ :
Cho tam giác ABC.Gọi $E, F, G$ là ba điểm tương ứng nằm trên $BC, CA, AB$. Ba đường thẳng $AE, BF, CG$ cắt nhau tại một điểm O khi và chỉ khi:
$\frac{AG }{GB}.\frac{BE}{EC}.\frac{CF}{FA}=1$
$\triangleright$ Chứng minh :

Toán thủ MSS 004
Phần thuận:
Giả sử ba đường thẳng $AE,BF,CG$ cắt nhau tại một điểm $O$.
TỪ $A$ và $C$, kẻ các đường song song với $BF$, chúng lần lượt cắt $CG$ và $AE$ tại $K, I$ tương ứng.
Ta có:$\frac{CF}{FA}=\frac{CO}{OK}$ và $\frac{CI}{AK}=\frac{CO}{OK}$ (Sử dụng định lý Thales)
$\Rightarrow \frac{CF}{FA}=\frac{IC}{AK}$.
Các cặp $\Delta$ đồng dạng $IEC$ và $OEB$, $AKG$ và $BOG$ : $\frac{BE}{CE}=\frac{BO}{CI}$ và $\frac{AG}{BG}=\frac{AK}{BO}$
Do đó: $\frac{AG }{GB}.\frac{BE}{EC}.\frac{CF}{FA}=\frac{AK}{OB}.\frac{BO}{IC}.\frac{IC}{AK}=1$
Phần đảo:
Giả sử ta có: $\frac{AG}{GB}.\frac{BE}{EC}.\frac{CF}{FA}=1$
Qua giao điểm của các đường thẳng $AE$ và $BF$, kẻ đường thẳng $CC_1$ với $C_{1}$ nằm trên cạnh $AB$. Khi đó, theo chứng minh phần thuận:
$\frac{AC_{1}}{C_{1}B}.\frac{BE}{EC}.\frac{CF}{FA}=\frac{AG }{GB}.\frac{BE}{EC}.\frac{CF}{FA}=1$
Suy ra $\frac{AC_{1}}{C_{1}B}=\frac{AG}{GB}$, hay $C_{1}\equiv G$, ta có điều phải chứng minh.
Bổ đề $\boxed{3}$ định lý Cê-va sin:
Gọi $E, F, G$ là ba điểm tương ứng nằm trên các đường thẳng $BC,CA,AB$ của $\Delta$ ABC. Ba đường thẳng $AE, BF, CG$ cắt nhau tại một điểm $O$ khi và chỉ khi: $\frac{sinABF}{sinCBF}.\frac{sinBCG}{sinACG}.\frac{sinCAE}{sinBAE}=1$
$\triangleright$ Chứng minh :

Toán thủ MSS 004
Phần thuận: Giả sử $AE, BF, CG$ đồng quy tại $O$.
Khi đó hai $\Delta$ $ABE$ và $ACE$ có cùng chiều cao hạ từ đỉnh $A$.
$\Rightarrow \frac{BE}{EC}=\frac{S_{ABE}}{S_{ACE}}=\frac{AB.AE.sinBAE}{AC.AE.sinCAE}=\frac{AB.sinBAE}{AC.sinCAE}$
Tương tự $\frac{CF}{FA}=\frac{BC.sinCBF}{BA.sinABE}$
Và $\frac{AG}{GB}=\frac{CA.sinACG}{CB.sinBCG}$
Nhân từng vế ba đẳng thức trên được:
$\frac{sinABF}{sinCBF}.\frac{sinBCG}{sinACG}.\frac{sinCAE}{sinBAE}=\frac{BE}{EC}.\frac{CF}{FA}.\frac{AG}{GB}=1$(Theo định lý Ceva)
Từ đó suy ra đpcm.
Phần đảo : Chứng minh tương tự phần thuân ta có $\frac{sinABF}{sinCBF}.\frac{sinBCG}{sinACG}.\frac{sinCAE}{sinBAE}=\frac{BE}{EC}.\frac{CF}{FA}.\frac{AG}{GB}$. Tới đây đưa về chứng minh bài toán đảo của định lý Cê-va (đã chứng minh ở bổ đề 2)
$\triangleright$ Trở lại bài toán :

$\triangleright$ Áp dụng bổ đề $\boxed{1}$ ta có :
$\dfrac{S_{AME}}{S_{AMF}}=\dfrac{\dfrac{1}{2}.AM.ME.sin \angle AME}{\dfrac{1}{2}.AM.MF.sin \angle AMF}=\dfrac{\dfrac{1}{2}.AM.AE.sin \angle MAC}{\dfrac{1}{2}.AM.AF.sin \angle MAB}\\\Rightarrow \dfrac{ME}{MF}=\dfrac{AE.sin \angle MAC}{AF.sin \angle MAB}$ (do $\angle AME+ \angle ADP=180 \Rightarrow \dfrac{sin \angle AME}{sin \angle ADP}=1$
$\Rightarrow \dfrac{sin \angle MAC}{sin \angle MAB}=\dfrac{ME}{MF}.\dfrac{AF}{AE}(1)$
Chứng minh một cách hoàn toàn tương tự ta cũng có :
$\frac{sin \angle NBA}{sin \angle NBC}=\frac{NF}{ND}.\frac{EC}{DC}(2)\\\\\frac{sin \angle PCB}{sin \angle PCA}=\frac{PD}{PE}.\frac{EC}{DC}(3)$
Từ $(1),(2),(3)\Rightarrow \frac{sin \angle MAC}{sin \angle MAB}.\frac{sin \angle NBA}{sin \angle NBC}.\frac{sin \angle PCB}{sin \angle PCA}=(\frac{ME}{MF}.\frac{NF}{ND}.\frac{PD}{PE}).(\frac{AF}{AE}.\frac{BD}{BF}.\frac{CE}{CD})$
$\triangleright$ Tiếp tục áp dụng bổ đề $\boxed{2}$ cho tam giác $ABC$ và $DEF$ ta có :
$\frac{AF}{AE}.\frac{BD}{BF}.\frac{CE}{CD}=1$
$\frac{ME}{MF}.\frac{NF}{ND}.\frac{PD}{PE}=1$
Như vậy ta đã chứng minh được: $\frac{sin \angle MAC}{sin \angle MAB}.\frac{sin \angle NBA}{sin \angle NBC}.\frac{sin \angle PCB}{sin \angle PCA}=1$
$\triangleright$ Áp dụng bổ đề $\boxed{3}$ ta có ngay điều phải chứng minh : $AM,BN,CP$ đồng quy.$\blacksquare$
$d=9$
$S= 40$
Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 16-03-2014 - 19:11