1.$\left\{\begin{matrix} x_{1}=2 & \\ x_{n}=\frac{x_{n-1}^2+2}{2x_{n}} & \end{matrix}\right.$
2.$\left\{\begin{matrix} u{1}=2 & \\ u_{n+1}=\frac{u_{n}^2}{2u_{n}-1} & \end{matrix}\right.$


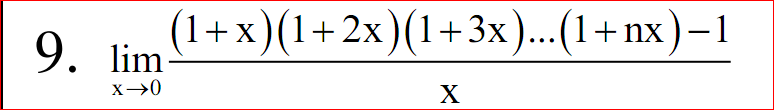
Niềm Tin + Hành Động = Thành Công
I Will Never Give Up
Tôi Yêu Bạn

Hướng dẫn $\prod_{k=1}^{n}\left ( 1+kx \right )=\left ( 1+x \right )\left ( 1+2x \right )...\left ( 1+nx \right )=1+\left ( 1+2+...+n \right )x+Bx^2$
Trong đó $B$ là một đa thức xác định.
$\text{Cứ làm việc chăm chỉ trong im lặng}$
 $\text{Hãy để thành công trở thành tiếng nói của bạn}$
$\text{Hãy để thành công trở thành tiếng nói của bạn}$

Hướng dẫn $\prod_{k=1}^{n}\left ( 1+kx \right )=\left ( 1+x \right )\left ( 1+2x \right )...\left ( 1+nx \right )=1+\left ( 1+2+...+n \right )x+Bx^2$
Trong đó $B$ là một đa thức xác định.
Cảm ơn bạn. Tức là GH đó =Vô cùng. bạn có thể giải thích rõ hơn cho mình cách phân thích như nào ra như vậy đc không? c/ơn bạn rất nhiều.
Niềm Tin + Hành Động = Thành Công
I Will Never Give Up
Tôi Yêu Bạn

1, Cho Un:
$U_{n}= \frac{2^3-1}{2^3+1}.\frac{3^3-1}{3^3+1}. ... .\frac{n^3-1}{n^3+1}$
Tìm lim Un.
2, Tìm lim$(\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{n(n+1)(n+2)})$
3, Tìm lim$(\frac{1}{1^2}+\frac{1}{2^2}+...+\frac{1}{n^2})$
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bài viết đã được chỉnh sửa nội dung bởi doilaphudu: 07-03-2014 - 22:48

bài 2
$\lim_{n\rightarrow \infty }\frac{1}{n(n+1)(n+2)}=\lim_{n\rightarrow \infty }\frac{1}{2}(\frac{n+2-n}{n(n+1)(n+2)})=\lim_{n\rightarrow \infty }\frac{1}{2}(\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)})=\lim_{n\rightarrow \infty }\frac{1}{2}(\frac{1}{2}-\frac{1}{6}+...-\frac{1}{(n+1)(n+2)})=\frac{1}{4}$
bài 3
hàm zeta, $\frac{\pi ^{2}}{6}$, bài này thì ko nằm trong phần thi đại học

Đặt $(1+x)(1+2x)(1+3x)...(1+nx)=A_{n}x^n+A_{n-1}x^{n-1}+A_{n-2}x^{n-2}+...+A_{2}x^2+A_{1}x+A_{0}=(A_{n}x^{n-2}+A_{n-1}x^{n-3}+A_{n-2}x^{n-4}+...+A_{2})x^2+A_{1}x+A_{0}=Bx^2+A_{1}x+A_{0}$
Trong đó :
Các hệ số $A_{i}$ ($i$ từ $2$ đến $n$) là các hằng số xác định (ta không quan tâm giá trị của chúng)
$A_{1}x=x.1.1...1+2x.1.1...1+3x.1.1...1+...+nx.1.1...1=(1+2+3+...+n)x\Rightarrow A_{1}=1+2+...+n=\frac{n(n+1)}{2}$
$A_{0}=1.1...1=1$
$B=A_{n}x^{n-2}+A_{n-1}x^{n-3}+A_{n-2}x^{n-4}+...+A_{2}$ là một đa thức xác định đối với biến $x$
Vậy :
$\lim_{x\rightarrow 0}\frac{(1+x)(1+2x)(1+3x)...(1+nx)-1}{x}=\lim_{x\rightarrow 0}\frac{Bx^2+A_{1}x}{x}$
$=\lim_{x\rightarrow 0}(Bx+A_{1})=A_{1}=\frac{n(n+1)}{2}$
Vậy đáp án bài này là $\frac{n(n+1)}{2}$ (chứ không phải là $+\infty$)
(Lưu ý rằng ta đang tìm giới hạn khi $x\rightarrow 0$ (chứ không phải khi $n\rightarrow \infty$).Còn $n$ trong bài này chỉ là một số nguyên dương xác định cho trước (xem như đã biết)
...
Ðêm nay tiễn đưa
Giây phút cuối vẫn còn tay ấm tay
Mai sẽ thấm cơn lạnh khi gió lay
Và những lúc mưa gọi thương nhớ đầy ...

1.Ta có: $x_{n}=\frac{x_{n-1}^{2}+2}{2x_{n}}\Leftrightarrow x_{n}^{2}=\frac{1}{2}x_{n-1}^{2}+1$
Đăt:$a_{n}=x_{n}^{2}-2$
$\Rightarrow \left\{\begin{matrix} a_{1}=x_{1}^{2}-2=2 & & \\ a_{n}+2=\frac{1}{2}(x_{n-1}+2)+1 & & \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a_{1}=2 & & \\ a_{n}=\frac{1}{2}a_{n-1}& & \end{matrix}\right.$
$\Rightarrow (a_{n})$ là một CSN với $a_{1}=2;q=\frac{1}{2}$
$\Rightarrow a_{n}=a_{1}q^{n-1}=2.\frac{1}{2^{n-1}}=\frac{1}{2^{n-2}}$
$\Rightarrow x_{n}^{2}=2+\frac{1}{2^{n-2}}$

1.$\left\{\begin{matrix} x_{1}=2 & \\ x_{n}=\frac{x_{n-1}^2+2}{2x_{n}} & \end{matrix}\right.$
2.$\left\{\begin{matrix} u{1}=2 & \\ u_{n+1}=\frac{u_{n}^2}{2u_{n}-1} & \end{matrix}\right.$
Giải:
$\left\{\begin{matrix} u_{1}=2 & \\ u_{n+1}=\frac{u_{n}^2}{2u_{n}-1}(1) & \end{matrix}\right.$
$(1)\Leftrightarrow \frac{1}{u_{n+1}}= \frac{1}{u_n}(2-\frac{1}{u_n})$
$(1)\Leftrightarrow x_{n+1}= - x_{n}^2 +2x_{n}$
Đến đây ta xét pt đặc trưng $-X^2 +2X=0$ là ra CTTQ ![]()
$$\mathfrak{Curiosity}$$

1, Cho $X_{n}$ xác định bởi:
$X_{1}=2014 $
$X_{n+1}= \frac{1}{4-3X_{n}} với \forall n\in N, n\geq 1$
2, Cho $X_{n}$ xác định bởi:
$X_{n}=a\in \left ( 1,2 \right )$
$X_{n+1}= 1+ X_{n}- \frac{1}{2}(X_{n})^2$
a, Chứng minh dãy có giới hạn
b, Tìm lim $X_{n}$
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

1, Cho $X_{n}$ xác định bởi:
$X_{1}=2014 $
$X_{n+1}= \frac{1}{4-3X_{n}} với \forall n\in N, n\geq 1$
2, Cho $X_{n}$ xác định bởi:
$X_{n}=a\in \left ( 1,2 \right )$
$X_{n+1}= 1+ X_{n}- \frac{1}{2}(X_{n})^2$
a, Chứng minh dãy có giới hạn
b, Tìm lim $X_{n}$









Đặt $y_n=x_n+1\Rightarrow y_{n+1}+1=\frac{1}{1-3y_n}\Rightarrow y_{n+1}=\frac{3y_n}{1-3y_n}$
Đặt $u_n=\frac{1}{y_n}\Rightarrow u_{n+1}=\frac{1}{3}u_n-1$
$\Rightarrow u_{n+1}+\frac{3}{2}=\frac{1}{3}\left(u_n+\frac{3}{2} \right)$
Đặt $v_n=u_n+\frac{3}{2}\Rightarrow v_{n+1}=\frac{1}{3}v_n\Rightarrow v_n$ là cấp số nhân....
$\Rightarrow ....$
0 thành viên, 0 khách, 0 thành viên ẩn danh