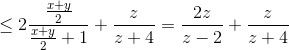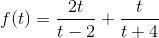1) Trước hết ta chứng minh $\frac{x}{x+1}+\frac{y}{y+1}\leq2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}$ với x, y > -1.
Sau khi biến đổi (với x, y > -1), bất đẳng thức trên tương đương với $(x-y)^2\geq0$.
Ta có:
$Q=\frac{x}{x+1}+\frac{y}{y+1}+\frac{z}{z+4}$
$\leq2\frac{\frac{x+y}{2}}{\frac{x+y}{2}+1}+\frac{z}{z+4}=\frac{2z}{z-2}+\frac{z}{z+4}$
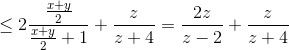
Ta có $x>-1$, $y>-1$ nên $z<2$.
Lập bảng biến thiên hàm 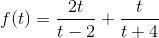 trong khoảng (-4,2), ta tìm được GTLN của Q là $\frac{1}{3}$, xảy ra $\Leftrightarrow x=y=\frac{1}{2}$, $z=-1$
trong khoảng (-4,2), ta tìm được GTLN của Q là $\frac{1}{3}$, xảy ra $\Leftrightarrow x=y=\frac{1}{2}$, $z=-1$
2) $x^2+y^2-2x-4y+4=0\Leftrightarrow (x-1)^2+(y-2)^2=1$. Đặt $x-1=a$, $y-2=b\Rightarrow a^2+b^2=1$
$|x^2-y^2+2\sqrt{3}xy-2(1+2\sqrt{3})x+(4-2\sqrt{3})y+4\sqrt{3}-3|=|a^2-b^2+2\sqrt{3}ab|$.
Theo BĐT Cauchy - Schwarz:
$|a^2-b^2+2\sqrt{3}ab|$
$\leq\sqrt{[(a^2-b^2)^2+4a^2b^2][1+(\sqrt{3})^2]}$
$=\sqrt{4(a^2+b^2)^2}=2$
Dấu bằng xảy ra $\Leftrightarrow a=\frac{\sqrt{3}}{2}$, $b=\frac{1}{2}$ hay $x=1+\frac{\sqrt{3}}{2}$, $y=\frac{5}{2}$
Nhận xét: Bài này có thể lượng giác hóa.
Bài viết đã được chỉnh sửa nội dung bởi RainThunde: 01-04-2014 - 02:45