Xét theo một cách nào đó thì những vấn đề như này cũng khá thú vị đấy chứ, thực tế có nhiều bạn học sinh (thậm chí là thầy cô giáo, nhất là người trẻ như mình) cũng còn chưa hiểu thật cặn kẽ những điều tưởng chừng như rất dễ kiểu thế này!
Bây giờ mình sẽ bổ sung thêm để lời giải của bạn buitudong1998 trọn vẹn hơn nhé!
Ta có $u^2+v^2=1$ nên $u\in[-1;1]$, do đó ta chọn được góc $\alpha$ để $u=\sin \alpha$.
Mà $\sin^2\alpha+\cos^2\alpha=1$ nên $\cos^2\alpha=1-\sin^2\alpha=1-u^2=v^2\Longleftrightarrow \left[ \begin{array}{l}\cos \alpha=v\\ \cos \alpha=-v\end{array}\right.$
Bây giờ ta sẽ xét hai trường hợp:
TH1: $v>0$.
Ta chọn góc $\alpha$ để $\sin \alpha=u$ nhưng $\alpha\in \left[ -\dfrac{\pi}2;\dfrac{\pi}2\right]$.
Luôn chọn được góc như thế (Xem hình vẽ)

Với góc $\alpha$ như này ta sẽ có $\cos \alpha>0$. Và do đó $\cos \alpha=v$
Như vậy ta đã chọn được góc $\alpha$ để $u=\sin \alpha$ và $v=\cos \alpha$.
TH2: $v<0$.
Ta chọn góc $\alpha$ để $\sin \alpha=u$ nhưng $\alpha\in \left[ \dfrac{\pi}2;\dfrac{3\pi}2\right]$.
Cũng luôn chọn được góc như thế (Xem hình vẽ)
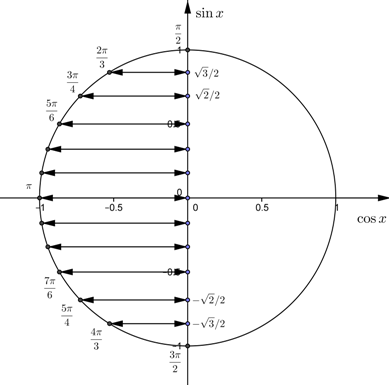
Với góc $\alpha$ như này ta sẽ có $\cos \alpha<0$. Và do đó $\cos \alpha=v$ (chú ý $v<0$ nhé.)
Như vậy ta cũng chọn được góc $\alpha$ để $u=\sin \alpha$ và $v=\cos \alpha$.
Nhận xét: Việc hiểu được cách ràng buộc điều kiện của góc $\alpha$ khi đặt $u=\sin \alpha$ mang rất nhiều ý nghĩa trong việc ứng dụng lượng giác vào các bài toán khác như giải phương trình chứa căn hoặc tính tích phân chẳng hạn.
![]() Có bạn nào giải thích giúp mình không?
Có bạn nào giải thích giúp mình không? ![]()
![]()
![]()














