Đề thi chọn đội tuyển toán THPT chuyên Đại học Sư Phạm Hà Nội năm học 2014-2015
Ngày 1:
Câu 1: Cho dãy số $\left ( x_n \right )^\infty _{n=1}$ thỏa mãn với $x_1=1$ và $x_{n+1}=5\left ( \sqrt{x_n+11}-\sqrt{x_n+4} \right )$ với mọi $n$ nguyên dương. Chứng minh rằng dãy số $\left ( x_n \right )^\infty _{n=1}$ có giới hạn hữu hạn và tìm giới hạn ấy.
Câu 2: Xét $M$ là tập tất cả các đa thức $p(x)=a_{2n}x^{2n}+a_{2n-1}x^{2n-1}+...+a_{1}x+a_0$ trong đó $n$ là số nguyên dương và $a_k$ là số thực thuộc đoạn $\left [ 100;101 \right ]$ với mọi $k=0,1,...,2n$
- Chứng minh rằng tồn tại đa thức $p(x)$ thuộc $M$ có bậc bằng 200 và có nghiệm thực.
- Tìm số nguyên dương $n$ nhỏ nhất thỏa mãn tính chất : tồn tại một đa thức $p(x)$ thuộc $M$ có bậc bằng $2n$ và có nghiệm thực.
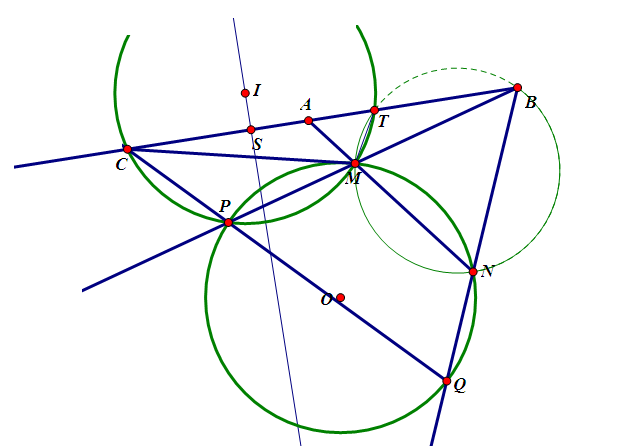
Câu 3: Cho tam giác $ABC$ . Đường tròn nội tiếp tam giác $ABC$ tiếp xúc với $BC$ ở $D$. $M$ là một điểm thay đổi trên $BC$ khác $B,C$. $(I_1),(I_2)$ theo thứ tự là đường tròn nội tiếp tam giác $ABM$ và $ACM$. $PQ$ là tiếp tuyến chung ngoài khác $BC$ của $(I_1),(I_2)$ (với $P\in\left ( I_1 \right )$ và $Q\in\left ( I_2 \right )$) . $S$ là giao điểm $BP$ và $CQ$. Chứng minh rằng :
- Bốn điểm $M,I_1,I_2,D$ cùng nằm trên một đường tròn.
- $S$ luôn chạy trên một đường tròn cố định.
Câu 4: Một bộ ba số nguyên được $(x,y,z)$ được gọi là một bộ ba $Pythagore$ nếu như $x^2+y^2=z^2$. Tìm số $k$ nhỏ nhất sao cho trong mỗi tập con gồm $k$ phần tử của tập $S=\left \{ 1,2,...,25 \right \}$, luôn có ba phần tử tạo thành một bộ ba $Pythagore$ .
Ngày 2:
Câu 5: Cho đường tròn $(O)$ và hai điểm $A,B$ phân biệt, cố định không thuộc đường tròn. Đường thẳng $\Delta$ thay đổi qua $A$ cắt đường tròn $(O)$ tại hai điểm phân biệt $M,N$. Gọi $P,Q$ là các giao điểm thứ hai của $BM,BN$ với $(O)$. Các đường thẳng $PQ$ và $AB$ cắt nhau ở $C$. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $MCP$ chạy trên một đường thẳng cố định.
Câu 6: Cho dãy số $\left ( x_n \right )_{n\geq 0}$ xác định bởi $x_0=0,x_1=3$ và $x_{n+1}=\frac{7x_n+3\sqrt{4+5x_n^2}}{2}$ với mọi số nguyên không âm $n$.
- Chứng minh rằng mọi số hạng của dãy $\left ( x_n \right )_{n\geq 0}$ là số tự nhiên và $x_{2014}$ chia hết cho $x_{19}$.
- Chứng minh rằng tồn tại số nguyên dương $a$ sao cho với mọi số nguyên dương $n$, trong biển diễn nhị phân của số $x_{an}$ có ít nhất $46^{2014}$ chữ số 1.
Câu 7: Cho $x,y,z$ là các số thực không âm và đôi một phân biệt. Chứng minh rằng: $$\frac{x+y}{\left ( x-y \right )^2}+\frac{y+z}{\left ( y-z \right )^2}+\frac{z+x}{\left ( z-x \right )^2}\geq \frac{9}{x+y+z}$$
Câu 8: Có một người sử dụng bản đồ trên điện thoại di động để đi từ một điểm $A$ đến một điểm $B$ . Anh ta đã đi đến được điểm $B$ sau một số lần cứ đi một đoạn thẳng lại phải chỉnh lại hướng bằng cách quay một góc nhọn theo chiều kim đồng hồ. Biết rằng tổng các góc phải điều chình này bằng $\alpha < 180^{\circ}$. Chứng minh rằng độ dài đoạn đường anh ta đi không vượt quá $\frac{AB}{cos\frac{\alpha }{2}}$.
Bài viết đã được chỉnh sửa nội dung bởi Trang Luong: 07-10-2014 - 19:14