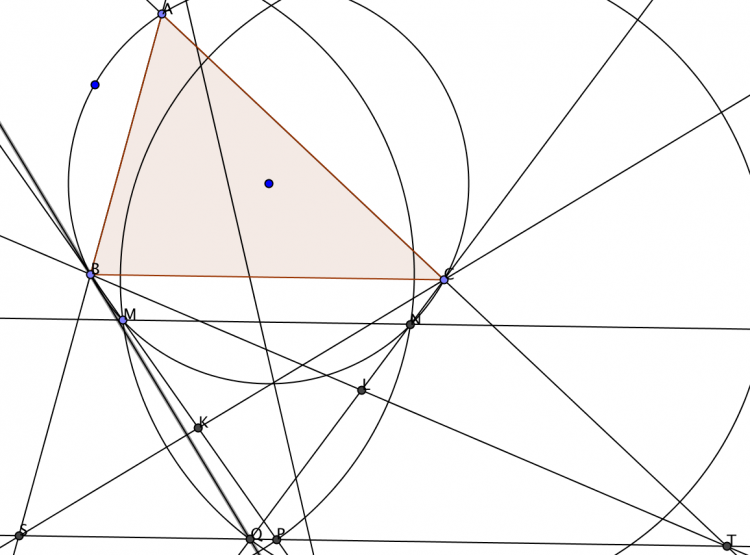
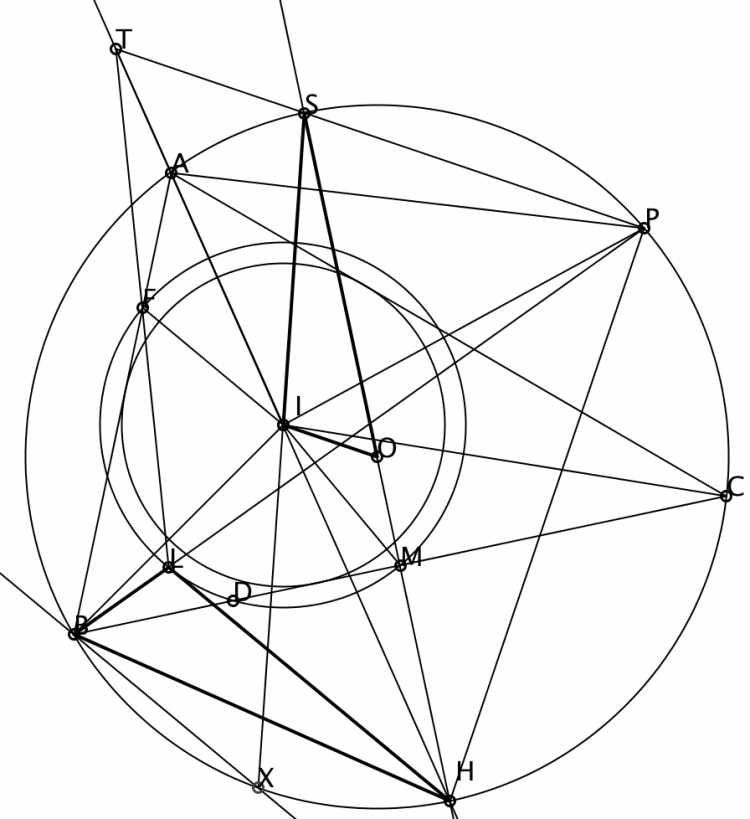
Bài 3: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Trên cung $BC$ không chứa A lấy hai điểm $M,N$ sao cho $MN//BC$ ( Tia $AM$ nằm giữa tia $AB$ và tia $AN$ ). Trên tia $BM,CN$ lấy điểm $P,Q$ sao cho $BP=BN=CM=CQ$. Đường thẳng $AM,AN$ cắt đường thẳng $PQ$ lần lượt tại $S,T$. $BT,CS$ lần lượt cắt cạnh $CQ,BP$ tại $L,K$. Chứng minh rằng $AK=AL$
Lời giải.
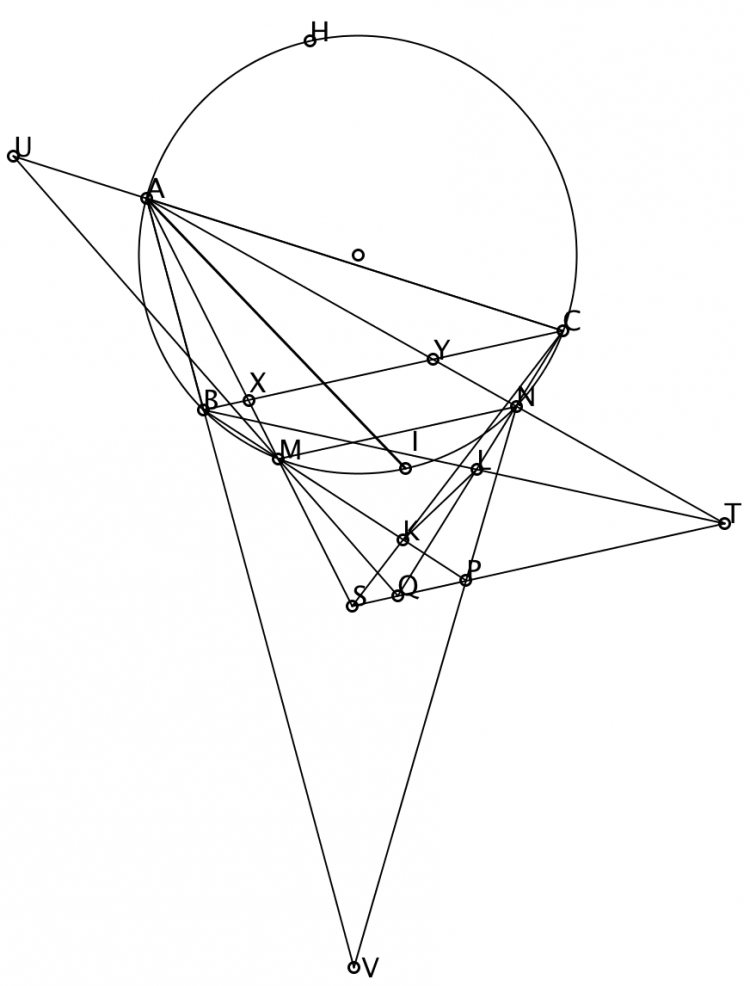
$AM,AN$ cắt $BC$ lần lượt tại $X,Y$. Dễ chứng minh $X,Y$ nằm giữa $BC$. Vì $BC \parallel SP$ nên $$\begin{aligned} & (BK,MP)=S(BK,MP)=(BC,X) \\ \Leftrightarrow & \frac{\overline{MB}}{\overline{PB}} \cdot \frac{\overline{PK}}{\overline{MK}}= \frac{\overline{XB}}{\overline{XC}} = \frac{AB \cdot \sin \left( \overrightarrow{AX}, \overrightarrow{AB} \right)}{AC \cdot \sin \left( \overrightarrow{AX}, \overrightarrow{AC} \right)} \end{aligned} \qquad (1)$$
Để ý rằng $ \frac{AB \cdot \sin \left( \overrightarrow{AX}, \overrightarrow{AB} \right)}{AC \cdot \sin \left( \overrightarrow{AX}, \overrightarrow{AC} \right)}= - \frac{AB}{AC} \cdot \frac{BM}{BP}$ vì $X$ nằm giữa $B$ và $C$. Kết hợp với $M$ nằm giữa $BP$ thì từ $(1)$ ta suy ra $\frac{\overline{PK}}{\overline{MK}}= - \frac{AB}{AC}$. Do đó $K$ nằm giữa $M$ và $P$ và $\frac{PK}{MK}= \frac{AB}{AC}$. Chứng minh tương tự $\frac{LN}{LQ}= \frac{AB}{AC}$ và $L$ nằm giữa $N,Q$. Khi đó $\frac{KP}{KM}= \frac{LN}{LQ}$ suy ra $KP=LN$ (vì $KP+KM=LN+LQ=QN=MP$).
Gọi $I$ là trung điểm cung $BC$ không chứa $A$. $CI$ phân giác $\angle MCN$ nên $CI \perp MQ,IM=IQ$ (vì $CM=CQ$). Tương tự $BI \perp PN,IN=IP$. Ta sẽ đi chứng minh $AI \perp KL$ và $IK=IL$.
Từ các chứng minh trên ta dễ dàng có $\triangle IPK= \triangle INL \; ( \text{c.g.c})$ dẫn đến $IK=IL$.
Ta có $\frac{KM}{KP}= \frac{LN}{LQ}= \frac{AB}{AC}$ nên $\overrightarrow{KL}= \frac{1}{AB+AC} \left( AC \cdot \overrightarrow{PN}+AB \cdot \overrightarrow{MQ} \right)$.
Ta có $$\begin{aligned} AI \perp KL & \Leftrightarrow \overrightarrow{AI} \cdot \overrightarrow{KL}= \vec{0} \\ & \Leftrightarrow \left( \overrightarrow{AB}+ \overrightarrow{BI} \right) \left( AC \cdot \overrightarrow{PN}+AB \cdot \overrightarrow{MQ} \right)= \vec{0} \\ & \Leftrightarrow \overrightarrow{AB} \cdot \overrightarrow{PN} \cdot AC + \overrightarrow{AI} \cdot \overrightarrow{MQ} \cdot AB = \vec{0} \; ( \text{ vì} \; BI \perp PN) \\ & \Leftrightarrow \overrightarrow{AB} \cdot \overrightarrow{PN} \cdot AC+ \overrightarrow{AC} \cdot \overrightarrow{MQ} \cdot AB= \vec{0} \; (\text{vì} \; CI \perp MQ) \\ & \Leftrightarrow AB \cdot PN \cdot AC \cdot \cos \left( \overrightarrow{PN}, \overrightarrow{AB} \right)= AC \cdot AB \cdot QM \cdot \cos \left( \overrightarrow{MQ}, \overrightarrow{AC} \right) \\ & \Leftrightarrow \cos \left( \overrightarrow{PN}, \overrightarrow{BA} \right)= \cos \left( \overrightarrow{MQ}, \overrightarrow{AC} \right). \end{aligned}$$
Trường hợp $A$ nằm chính giữa cung $BC$ thì ta dễ dàng chứng minh được $AK=AL$, lúc này $AB \parallel NP, AC \parallel MQ$.
Trường hợp $A$ không nằm chính giữa cung $BC$, gọi giao điểm của các cặp đưởng thẳng $PN$ và $AB$, $MQ$ và $AC$ lần lượt là $U,V$. Dễ chứng minh được $\angle CVM= \angle AUN= \left| \angle ABC- \angle ACB \right|$. Ta sẽ chứng minh $U,V$ nằm trên hai nửa mặt phẳng đối nhau bờ $BC \qquad (2)$.
Gọi $H$ là điểm chính giữa cung $BC$ chứa điểm $A$. Khi đó $HC \parallel QM$. Không mất tính tổng quát, giả sử $AB<AC$ thì khi đó $A,B,M,Q$ cùng nằm trên một nửa mặt phẳng bờ $HC$. Do đó với $V$ là giao điểm của $AB$ và $MQ$ thì $A$ nằm giữa $V$ và $C$. Hay nói cách khác $V$ nằm trên nửa mặt phẳng bờ $BC$ có chứa $A$. Lập luận tương tự với $U$. Ta đã chứng minh được $(2)$. Trong trường hợp $AB<AC$ thì áp dụng $(2)$ ta được $A$ nằm giữa $V$ và $C$, $M$ nằm giữa $V$ và $Q$ nên $\left( \overrightarrow{MQ}, \overrightarrow{AC} \right)= \angle CVM$.
Từ $(2)$ ta suy ra $\cos \left( \overrightarrow{MQ}, \overrightarrow{AC} \right) = \cos \angle CVM = \cos \left( \overrightarrow{PN}, \overrightarrow{BA} \right)$ (trường hợp $AB<AC$). Ta thu được $AI \perp KL$.
Vậy $AI \perp KL$ và $IK=IL$ nên ta suy ra $AK=AL$. $\blacksquare$
Ps: Xin lỗi vì kí hiệu nhầm trong hình vẽ, hai điểm $U,V$ đổi tên cho nhau nhé! 
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 18-10-2014 - 17:17