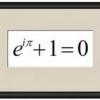gpt: $3^x+4^x=5^x$
gpt $3^x+4^x=5^x$
#1
 Đã gửi 08-11-2014 - 15:33
Đã gửi 08-11-2014 - 15:33

Tương lai khóc hay cười phụ thuộc vào độ lười của quá khứ
#2
 Đã gửi 08-11-2014 - 15:39
Đã gửi 08-11-2014 - 15:39

gpt: $3^x+4^x=5^x$
$\Leftrightarrow 9^{\frac{x}{2}}+16^{\frac{x}{2}}=25^{\frac{x}{2}}\Leftrightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}+\left ( \frac{16}{25} \right )^{\frac{x}{2}}=1$
Nếu $x\geq 2$ thì
Vì $\frac{9}{25}< 1\Rightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}\leq\frac{9}{25}$
tương tự suy ra $VT\leq1$
đẳng thức xả ra khi và chỉ khi $x=2$
Nếu $x\leq 2$ thì $\frac{9}{25}< 1\Rightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}>\frac{9}{25}$
suy ra $x=2$
Bài viết đã được chỉnh sửa nội dung bởi ChiLanA0K48: 08-11-2014 - 23:13
- Rikikudo1102 và PolarBear154 thích
#3
 Đã gửi 08-11-2014 - 16:03
Đã gửi 08-11-2014 - 16:03

$\Leftrightarrow 9^{\frac{x}{2}}+16^{\frac{x}{2}}=25^{\frac{x}{2}}\Leftrightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}+\left ( \frac{16}{25} \right )^{\frac{x}{2}}=1$
Vì $\frac{9}{25}< 1\Rightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}\leq\frac{9}{25}$
tương tự suy ra $VT\leq1$
đẳng thức xả ra khi và chỉ khi $x=2$
Bài này mình chia luôn
${3^x} + {4^x} = {5^x} \Leftrightarrow {\left( {\frac{3}{5}} \right)^x} + {\left( {\frac{4}{5}} \right)^x} = 1$
sau đó đánh giá
- Rikikudo1102 yêu thích
#4
 Đã gửi 08-11-2014 - 18:32
Đã gửi 08-11-2014 - 18:32

$\Leftrightarrow 9^{\frac{x}{2}}+16^{\frac{x}{2}}=25^{\frac{x}{2}}\Leftrightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}+\left ( \frac{16}{25} \right )^{\frac{x}{2}}=1$
Vì $\frac{9}{25}< 1\Rightarrow \left ( \frac{9}{25} \right )^{\frac{x}{2}}\leq\frac{9}{25}$
tương tự suy ra $VT\leq1$
đẳng thức xả ra khi và chỉ khi $x=2$
Bạn đánh giá bị sai rồi. Giả sử $x=1$ thì $(\frac{9}{25})^{\frac{1}{2}}> \frac{9}{25}$.
Bài viết đã được chỉnh sửa nội dung bởi Lam Ba Thinh: 08-11-2014 - 18:34
- ChiLanA0K48 yêu thích
#5
 Đã gửi 08-11-2014 - 22:53
Đã gửi 08-11-2014 - 22:53

Bài này phải đánh giá theo hai hướng:
$x > 2$: VT lớn hơn 5
$x < 2$: VT bé hơn 5
Bài viết đã được chỉnh sửa nội dung bởi SilentAssassin1998: 08-11-2014 - 23:15
- ChiLanA0K48 yêu thích
The 7 wonders
${1729}$
${381654729}$
${142857}$
${2520}$
${12345679}$
?
?
#6
 Đã gửi 08-11-2014 - 23:09
Đã gửi 08-11-2014 - 23:09

Bài này mình chia luôn
${3^x} + {4^x} = {5^x} \Leftrightarrow {\left( {\frac{3}{5}} \right)^x} + {\left( {\frac{4}{5}} \right)^x} = 1$
sau đó đánh giá
Bạn đánh giá bị sai rồi. Giả sử $x=1$ thì $(\frac{9}{25})^{\frac{1}{2}}> \frac{9}{25}$.
Mình có ý chia xuống cho chẵn thôi ![]() nhưng đánh giá của mình vẫn chưa đúng. Hình như phải đánh giá như bạn SilentAssassin1998 mới đúng
nhưng đánh giá của mình vẫn chưa đúng. Hình như phải đánh giá như bạn SilentAssassin1998 mới đúng ![]() Chp phép mình sửa bài giải trên nhé!
Chp phép mình sửa bài giải trên nhé!
Bài viết đã được chỉnh sửa nội dung bởi ChiLanA0K48: 08-11-2014 - 23:14
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh