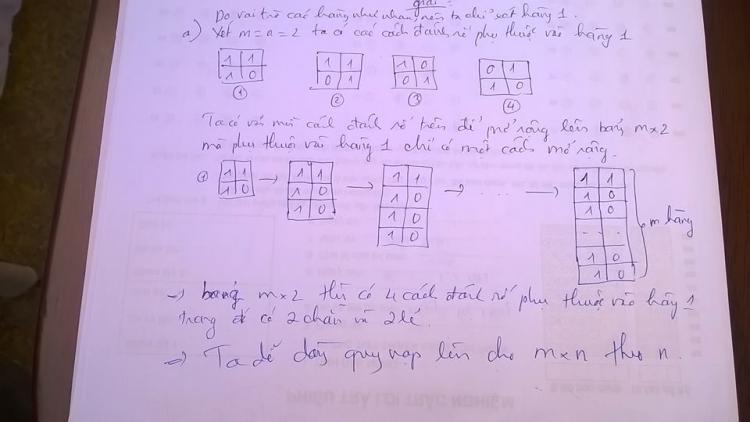Chủ đề này có 32 trả lời

[cachuoi]

vẫn tìm ra cttq như cậu rồi làm tiếp , xét phương trình x^3-x^2+x=0 có 3 nghiệm trong đó có 2 nghiệm phức đặt là z1 và z2 
1 nghiệm thực là x=0
do vậy muốn f_n(x)chia hết cho x^3-x^2+x
nên f_n(0)=0 do vậy n lẻ 
tương tự f_n(z1)=f_n(z2)=0 
thay số vụ thể vào rồi quy nạp 3/n 
ngoài ra còn 1 cách khác mình đọc đc trên mạng là dùng công thức moivre là nhanh nhất

[taideptrai]

bạn khanghaxuan làm sai rồi, đáp số là n lẻ và là bội của 3

[taideptrai]

Bài 1   :    $\left\{\begin{matrix} f_{0}(x)=2 , f_{1}(x)=3x & \\ f_{n}(x)=3xf_{n-1}(x)+(1-x-2x^{2})f_{n-2}(x) & \end{matrix}\right.$  

 

Áp dụng phương pháp sai phân bậc 2 ta tìm được công thức tổng quát :   

 

                                              $f_{n}(x)=(2x-1)^{n}+(x+1)^{n}$   
 

Khai triển rồi nhóm lại ta được :   

 

        $f_{n}(x)=x^{n}.(2^{n}+1)+...+(-1)^{n}+1^{n}$  (*)

 

 Để (*) chia hết cho  $x^{3}-x^{2}+x$  thì $n$ là một số lẻ và được viết dưới dạng sau :  

 

$x(x^{2}-x+1)(x^{n-3}.C_{1}+....+x.C_{n-3}+C_{n-2})$

 

Xét đa thức $g(x)=x^{n-1}(2^{n}+1 )+...+C^{n-1}_{n}$ 

                    

                     $h(x)=x^{3}.C_{1}+...+C_{n-2}$

 

Ta có :  Tổng các hệ số của đa thức $g(x)$ bằng tổng hệ số của đa thức $h(x)$ (  $h(x)$ là đa thức thương của $g(x)$ với $x^{2}-x+1$ 

 

Ta xác định được :   $C_{1}=2^{n}+1$ 

                                 $C_{n-2}=C^{n-1}_{n}$

 

Tới đây bước tính toán của em hơi khủng !!!!! 

 

$C_{3}=C^{2}_{n}(2^{n-2}-1)+C^{1}_{n}(2^{n-1}+1)$ 

$C_{4}=C^{3}_{n}(2^{n-3}-1)+C^{2}_{n}(2^{n-2}+1)-2^{n}-1$

 

Cứ tiếp tục như thế  (  Khúc sau khủng quá nên lười ghi )

 

Cuối cùng cân bằng hệ số giữa  $C_{n-2}$  trong khai triển trên với $C_{n-2}$ trong đa thức $g(x)$

 

Ta tìm được :  $n=3$ thỏa đề bài .  

 

P/s : Cái khúc tính toán để em xem lại nhé ! ( Dấu $+$ , $-$  loạn xạ ) 

sai rồi bạn ơi!!! n là số lẻ chia hết cho 3, bài này dùng hằng đẳng thức đáng nhớ

Bài viết đã được chỉnh sửa nội dung bởi taideptrai: 10-01-2015 - 22:17

[taideptrai]

Bài 1 :  

 

a.  Với $a=0$ thì dãy viết lại như sau :         $\left\{\begin{matrix} u_{1}=3 & \\ u_{n+1}=\frac{1}{2}u_{n}+\frac{1}{4}\sqrt{u^{2}_{n}+3} & \end{matrix}\right.$

 

     Th1:   $$u_{n}\in \begin{bmatrix} 1;\infty \end{bmatrix}$$  (**)

 

Xét  $u_{n+1}-u_{n}=\frac{1}{4}\sqrt{u^{2}_{n}+3}-\frac{u_{n}}{2}$ (*)

 

Giả sử $u_{n}$  là hàm tăng thì (*) $\Leftrightarrow \sqrt{u^{2}_{n}+3} >  2u_{n}\Leftrightarrow u_{n}<1$  ( vô lý ) 

 

nên $u_{n}$ là hàm giảm  mà kết hợp với (**) nên $u_{n}$ có giới hạn hữu hạn .   

 

Gọi    $lim u_{n}=L$   ,  chuyển qua giới hạn ta có :    $L=1$  nên    $lim u_{n}=1$

 

  Hiển nhiên ta có $u_{n}>0$ 

 

 Th2 :        $0< u_{n}\leq 1$ (***)  ,  tương tự như trên ta cũng chứng minh được  $u_{n}$ là hàm số tăng mà kết hợp với  (***)

 

ta được  $u_{n}$ tăng và bị chặn trên nên    $lim u_{n}=1$

 

b.         Th1 :   $u_{n}\in \begin{bmatrix} 1;\infty \end{bmatrix}$  ,  chứng minh tương tự câu a  nên dãy có giới hạn hữu hạn 

 

            Th2 :   $0 < u_{n}\leq 1 $  ta cũng sẽ chứng minh $u_{n}$ là hàm tăng như sau :      

 

Xét :  $u_{n+1}-u_{n}=\frac{n^{2}}{4n^{2}+a}\sqrt{u^{2}_{n}+3}-\frac{1}{2}u_{n}$

 

Sau đó sử dụng đánh giá  :   $a <1$  rồi đưa về biểu thức sau :   $u^{2}_{n}=\frac{12n^{4}}{12n^{4}+8n^{2}+1}<1 \rightarrow u_{n}<1$  (đúng )

 

nên $u_{n}$  tăng và bị chặn trên nên  $u_{n}$ có giới hạn hữu hạn 

Câu a của cậu cũng sai luôn rồi!!! Có đến mấy chỗ cậu ngộ nhận luôn. Làm gì có chuyện hàm không tăng thì là hàm giảm??? Nếu như xét TH như vậy thì đang còn thiếu TH, lỡ dãy nãy đánh võng quanh số 1 thì cậu làm sao???

[duythanbg]

Câu 4b

Goi (ABC) là (O) tâm O

Gọi giao điểm của TM,TN với (O) là L,G

Ta sẽ chứng minh phân giác MTN đi qua điểm chính giữa cung BC không chứa A.  Tương đương với chứng minh LG // BC hay $\widehat{BTM}=\widehat{NTC}$  (5)

Dễ thấy PQ là trục đẳng phương của (I),(HBC),(K) .                 (*)

Gọi J là giao điểm của EF với BC .

Ta có EFBC nội tiếp nên JE.JF=JB.JC do đó J nằm trên trục đẳng phương của (HBC) hay (O) và (I)     

Do đó J,P,Q thẳng hàng .

Ta có : T nằm trên trục đẳng phương của (O) và (K) nên O,K,T thẳng hàng .                 (1)

  Từ (*) suy ra  : JE.JF = JP.JQ = JM.JN = JB.JC

Do đó J nằm trên trục đẳng phương của (O) và (K) .                                                        (2)

Từ (1) và (2) suy ra JT tiếp xúc (O) , (K).

 

Dễ thấy : $\widehat{JTC}=\widehat{TBC}$                                        (3)

     $ JT^2=JB.JC=P_{J/(O)} $ 

 

Do đó : $\widehat{JTN}=\widehat{JMT}$                                           (4)

 

Từ (3) và (4) suy ra ĐPCM  (Theo (5))

Bài viết đã được chỉnh sửa nội dung bởi duythanbg: 13-01-2015 - 22:36

[quyenlan1250]

 LOI GIAI DE THI VMO 2015.pdf   132.77K   484 Số lần tải

Đây là lời giải của câu 3 ngày 1 theo số phức 

[LilTee]

5 cách giải câu Bất đẳng thức

File gửi kèm

•  Lời giải Bất đẳng thức trong đề thi HSG Quốc gia môn Toán 2015 - Tăng Hải Tuân.pdf   84.13K   409 Số lần tải

[quyenlan1250]

Bài 7đề thi VMO 2015 câu a

[quyenlan1250]

lời giải bài 5

Hình gửi kèm

• 
• 
• 
• 
• 
• 

[quyenlan1250]

Bài này dùng đồng dư giải cũng được bạn ah.

[shinichigl]

 

NGÀY 2

Bài 5: (7,0 điểm) Cho $(f_n(x))$ là dãy đa thức xác định bởi:

$f_0(x)=2,f_1(x)=3x,f_n(x)=3xf_{n-1}(x)+(1-x-2x^2)f_{n-2}(x)$ với mọi $n\ge 2$. 

Tìm tất cả các số nguyên dương $n$ để $f_n(x)$ chia hết cho đa thức $x^3-x^2+x$.

Áp dụng phương trình sai phân bậc hai, ta tìm được công thức tổng quát: $f_{n}(x)=(2x-1)^{n}+(x+1)^{n}$ (*)

Thay $x=5$ vào (*) ta được $f_{n}(5)=9^{n}+6^{n}$

Ta sẽ tìm $n$ để $f_{n}(5)=9^{n}+6^{n}$ chia hết cho $5^{3}-5^{2}+5=105$

Ta có $9^{n}+6^{n}=3^{n}\left ( 3^{n}+2^{n} \right )$ và $105=3.5.7$

Suy ra ta chỉ cần tìm $n$ sao cho $3^{n}+2^{n}$ chia hết cho $7$

Đặt $n=6k+r$ ($r\in \left \{ 0,1,2,3,4,5 \right \}$)

Từ đó ta có $3^{n}+2^{n}=3^{6k+r}+2^{6k+r}=729^{k}.3^{r}+64^{k}.3^{r}$

Suy ra $3^{n}+2^{n}\equiv 3^{r}+2^{r}(mod7)$

Lần lượt thay $r= 0,1,2,3,4,5$ ta thấy chỉ có $r=3$ thõa mãn $3^{n}+2^{n}\equiv 0(mod7)$

Tiếp theo ta sẽ chứng minh $n=6k+3$ thõa mãn (bằng quy nạp theo $k$)

Thật vậy,

Với $k=0$ ($n=3$) ta có $f_{n}=f_{3}=9x^{3}-9x^{2}+9x$ chia hết cho $x^{3}-x^{2}+x$

Giả sử $k=a$ thõa mãn, ta sẽ chứng minh $k=a+1$ cũng thõa mãn

Ta có 

$(2x-1)^{6a+9}+(x+1)^{6a+9}=\left [ (2x-1)^{6a+3}+(x+1)^{6a+3} \right ]\left [ (2x-1)^{6}+(x+1)^{6} \right ]-(2x-1)^{6}(x+1)^{6}\left [ (2x-1)^{6a-3}+(x+1)^{6a-3} \right ]$

chia hết cho $x^{3}-x^{2}+x$

Vậy theo nguyên lý quy nạp ta có $n=6k+3$, với mọi $k$ nguyên không âm, thõa mãn đề bài

Bài viết đã được chỉnh sửa nội dung bởi shinichigl: 18-01-2015 - 13:23

[quyenlan1250]

 BINH LUAN DE THI VMO 2015.doc   201K   323 Số lần tải

Bình luận bài 3 và bài VMO 2015

[quyenlan1250]

Lời gải bài 3 trước có nhầm lẫn mình đã gửi lời giải bài 3 và bài 7