George Boole
(1815 - 1864)
Năm 2015 là một năm đặc biệt đối với các nhà toán học: Kỉ niệm 200 năm ngày sinh của George Boole - một trong những người phát minh ra máy tính hiện đại ngày nay.
Câu chuyện về George Boole (1815-1864) là một ví dụ khác thường về một nhà khoa học trong suốt nhiều thế kỉ. Những nghiên cứu của ông đã xây dựng một nền tảng cho máy tính và điện thoại thông minh ngày nay. Tuy nhiên, ông đã mất trước khi chiếc máy tính đầu tiên ra đời. Vậy, làm sao mà một nhà toán học trong thế kỉ XIX và các nghiên cứu của ông lại có thể ảnh hưởng đến nền khoa học công nghệ thế kỉ XXI? Dưới đây là câu chuyện về ông - George Boole và những kỹ sư thời hiện đại đã nhận ra sức mạnh trong ý tưởng của ông.
I. LÚC CÒN TRẺ
Lúc trẻ, George Boole đã không để lại dấu ấn gì đột phá dưới vai trò của một nhà toán học. Sinh ra tại Lincoln vào năm 1815, ông là con của một thợ đóng giày địa phương. Tưởng như ông sẽ kế tục gia đình làm việc trong lĩnh vực kinh doanh giày da, tuy nhiên, do công ty của nhà ông sụp đổ, ông đã trở thành một thầy giáo. Ở tuổi 19, Boole vẫn là một thầy giáo chủ nhiệm, mặc dù vậy hầu như ông dành tất cả các buổi tối và ngày nghỉ của mình để tìm tòi khám phá những ý tưởng toán học! Tác phẩm đầu tay của ông đã xuất hiện tại the Cambridge Mathematics Journal và công việc của ông đã thu hút được sự chú ý của Hội đồng Hoàng Gia. Năm 1844, Boole được trao tặng Huân chương Hoàng Gia cho bài báo về Công thức tổng quát của Giải tích (On a general method of analysis). Hồ sơ phát triển của ông đã giúp ông được đề nghị trở trở thành Giáo sư ngay sau đó. Boole bỏ lại sự nghiệp dạy học của mình tại Lincoln và chuyển đến Đại học Cork, dành toàn bộ đời mình để theo đuổi toán học và thực hiện những nghiên cứu đột phá mà thành quả của nó vẫn còn tác động đến cuộc sống quanh ta hôm nay.
II. NHỮNG PHÁT HIỆN QUAN TRỌNG
Trong những năm tại Ireland, Boole tập trung vào việc kết hợp suy diễn logic với đại số. Ông cho rằng cách tiếp cận logic của các nhà triết học Hi Lạp cổ đại như Aristotle và những người cùng trường phái là không đủ để giải quyết một số vấn đề. Ộng tập trung vào những vấn đề mà mỗi câu phát biểu hoặc mệnh đề chỉ có thể mô tả dưới dạng đúng hoặc sai. Công việc của Boole đòi hỏi sự phát triển của một ngành toán học mới trong đại số và các qui tắc số học xung quanh nó.
Để giới thiệu cho ý tưởng của Boole, ta xem xét hai mệnh đề sau:
A = David Beckham là một cầu thủ.
B = Cưỡi chổi là một môn thể thao Olympic.
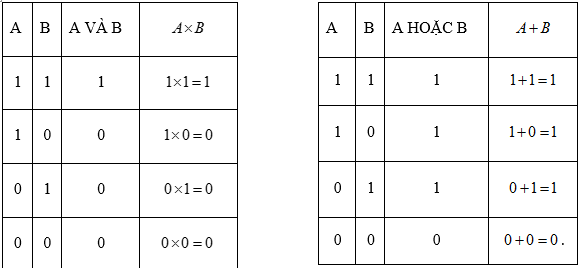
Rõ ràng chúng ta biết được trong số hai mệnh đề trên, sẽ có một mệnh đề đúng và một mệnh đề sai (bạn có thể tự nhận ra!). Tuy nhiên nếu ta phát biểu “A và B” tức là “David là cầu thủ và cưỡi chổi là môn thể thao” thì rõ ràng điều này là sai! Vậy nếu phát biểu trên là đúng thì ta cần mỗi thành phần trong câu đó đều đúng, và trường hợp đó không xảy ra. Vì vậy, tuyên bố “A và B” là sai. Mô hình hóa: Nếu chúng ta gán giá trị chân trị bằng 0 cho một mệnh đề sai và 1 cho một mệnh đề đúng, sau đó ta coi liên kết “và” là một phép nhân trong đó “AB” là viết tắt của “A và B”, vậy để xét tính đúng sai ta xem xét tích số chân trị $1\times 0=0$.
Vậy còn mệnh đề “A hoặc B”? Hoặc David là một cầu thủ hoặc cưỡi chổi là môn thể thao? Với điều này chỉ cần hoặc A đúng, hoặc B đúng thì cả mệnh đề sẽ đúng. Mô hình hóa như trên ta viết lại : “$A+B$” như là viết tắt của “A hoặc B”, vậy giá trị chân trị của $A+B$ là giá trị $1+0=1$.
Những ý tưởng này vẫn thỏa nếu A và B hoán đổi giá trị chân trị của mỗi mệnh đề, hoặc nếu chúng cùng đúng hay cùng sai. Bảng dưới đây cho ta thấy các giá trị chân trị cho mệnh đề “A và B”, “A hoặc B” cho mọi bộ giá trị của A, B kết hợp lại. Điều đó cho thấy định nghĩa của Boole về các phép tính đại số tương ứng. Điều duy nhất làm cho đại số Boole khác với các loại chúng ta đang sử dụng chính là theo Boole, “$1+1=1$” chứ không phải là “$1+1=2$”, tuy nhiên điều này không quá khó khăn để làm quen với các tính chất đặc trưng của chúng.
Theo Boole, tất cả các câu logic, các phát biểu đều được cấu thành từ các mệnh đề nhỏ hơn, và chúng được nối với nhau qua các toán tử “và” hay “hoặc”, và dĩ nhiên cũng có toán tử “không”, biến các giá trị chân trị thành trị đối lập của nó. Nếu ta nói mệnh đề “David là cầu thủ bóng đá” là đúng thì phủ định (toán tử “không”) sẽ xác định “ David không phải là cầu thủ bóng đá” là sai.
Bây giờ bạn đã nắm rõ được qui luật của đại số Boole, chắc bạn sẽ thích vấn đề dưới đây:
“Tưởng tượng rằng tôi có 3 quầy X, Y và Z, tuy nhiên chúng không được xếp đúng thứ tự này. Có một và chỉ một mệnh đề dưới đây là chính xác:
X màu đỏ
Y không phải màu đỏ
Z không phải màu xanh
Liệu bạn có thể tìm ra chính xác màu sắc của từng quầy?”
Mặc dù có nhiều cách giải quyết vấn đề này, chẳng hạn như thử một vài trường hợp và tìm ra qui luật. Tuy nhiên, Boole cho rằng có một cách tiếp cận có hệ thống và có thể giải quyết một lượng vấn đề lớn hơn, phức tạp hơn. Đối với bài toán trên, có lẽ bạn đã nhận ra các mệnh đề quan trọng giúp bạn giải quyết vấn đề. Ví dụ X có thể là màu Đỏ, Trắng hoặc Xanh, do đó mệnh đề “X Đỏ hoặc X Trắng hoặc X Xanh” là đúng với chân trị là 1. Tương tự vậy, các mệnh đề “X Đỏ hoặc Y Đỏ hoặc Z Đỏ” cũng có trị 1, hiển nhiên mỗi màu chỉ ở một quầy và một quầy chỉ có một màu nên các mệnh đề như “X và Y màu Đỏ” hay “ X màu Xanh và Trắng” đều sai nên nhận trị 0.
Với phương án này, tôi sẽ đễ bạn thiết lập các định đề và sử dụng phương pháp tiếp cận kiểu Boole để giải quyết vấn đề trên.
III. SỰ PHỐI HỢP XUYÊN THẾ KỈ
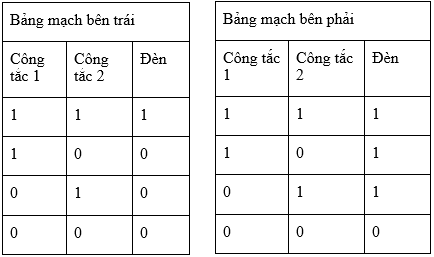
Hơn 70 năm sau cái chết của Boole, cách tiếp cận nhị phân (chỉ với hai kí số 1 và 0) đã tìm được một ứng dụng mạnh mẽ, khi mà các nhà toán học và kĩ sư như Claude Shannon nhận ra rằng các kí số này mô tả mạch điện một cách hoàn hảo. Đễ hình dung ra vấn đề này, ta tưởng tượng một mạch điện với hai bộ phận chuyển mạch và một bóng đèn gắn liền trong mạch. Bóng đèn sẽ sáng lên nếu có dòng điện đi qua, ngược lại thì đèn tắt. Mỗi công tắc có thể đóng (bật) hoặc mở (tắt). trong hình bên trái phía dưới, đèn sẽ sáng lại nếu nếu cả hai công tắc đang đóng. Trong hình bên phải, đèn sẽ sang nếu một trong hai công tắc được bật lên.
Các kĩ sư (trong đó có Shannon) nhận ra rằng họ có thể đặt kí số 1 cho trạng thái bóng đèn “bật” và 0 cho trạng thái bóng đèn “tắt”. Viết rõ ra các kết hợp 0 và 1 cho các thiết bị công tắc và trạng thái tương ứng của đèn, bạn nhận được chính xác bảng chân trị của “Hoặc” với bảng mạch bên trái, “Và” với bảng mạch bên phải.
Việc sử dụng một công tắc biến tần cho phép dòng điện đi qua khi công tắc mở, bạn có thể mô phỏng lại các bảng chân trị của phép “Phủ định”.
Thực hiện việc này mang một ý nghĩa quan trong đối với các kĩ sư khi họ có thể sử dụng phương pháp đại số Boole trong việc đơn giản hóa các mạch phức tạp.
Không dừng lại ở đó, Shannon vẫn còn tiến xa hơn: ông đề nghị rằng mọi loại thông tin (bao gồm cả từ ngữ lẫn hình ảnh, âm thanh) có thể được mô tả bằng các chuỗi số 0 và 1 (trong thực tế, Shannon cũng đã đề xuất phổ biến các chuỗi bit mà chúng ta thường dùng để mô tả chữ số ngày nay). Vì việc có thể dễ dàng mô tả các mệnh đề “Và”,“Hoặc”,”Không” cho các mạch điện tử, bạn có thể thực hiện các công việc mang tính logic lien quan đến xử lý thông tin. Đó là cơ sở để các bộ xử lý trung tâm (CPU) hiện nay phát triển lên.
Dù thế nào đi nữa, không thể phủ nhận được rằng những tiện ích bạn đang sử dụng ngày nay đều dựa trên hệ thống nhị phân và phương pháp đại số logic Boole - một người đàn ông đã sống, đã chết nhiều năm trước khi bóng đèn được tung vào thị trường và đóng một vai trò then chốt trong sự phát triển mạch điện hiện đại của chúng ta ngày nay.
Nguồn: https://plus.maths.o...nt/george-boole
Người dịch: Nguyễn Văn Sáng Hồng - Thành viên Chuyên san EXP.