Chủ đề này có 13 trả lời

[Phanbalong]

Đề hơi mờ mọi người thông cảm

Hình gửi kèm

• 

[Hoang Nhat Tuan]

Đề hơi mờ mọi người thông cảm

Câu 1: Chuẩn hóa $a+b+c=3$, khi đó BĐT trở thành:

$\sum (\frac{a}{3-a}+\sqrt{\frac{a}{2(3-a)}})\geq 3$

Lại có: $\frac{a}{3-a}+\sqrt{\frac{a}{2(3-a)}}=\frac{2a+\sqrt{2a(3-a)}}{2(3-a)}\geq \frac{9}{8}a-\frac{1}{8}$

Thiết lập 2 BĐT tương tự rồi cộng lại suy ra ĐPCM

[Quoc Tuan Qbdh]

Đề hơi mờ mọi người thông cảm

 

Sở GD&ĐT NGHỆ AN                                                                     KÌ THI CHỌN ĐỘI TUYỂN DỰ THI HSG QUỐC GIA

                                                                                                                     BẬC THPT NĂM HỌC 2015-2016

                                                                      

                                                                                Môn thi : Toán

                                                                               Thời gian làm bài : 180 phút

                                                                                Ngày thi : 06/10/2015

Câu $1$ ($5,0$ điểm)

Cho $3$ số dương $a;b;c$ chứng minh rằng :

$\sum \frac{a}{b+c}+ \sum \sqrt{\frac{a}{2b+2c}} \geq 3$

 

Câu $2$ ($5,0$ điểm)

Tìm tất cả các số tự nhiên $a$ sao cho tồn tại số nguyên dương $n$ lớn hơn $1$ và thỏa mãn $a^{n}+1$ chia hết cho $n^{2}$

 

Câu $3$ ($5,0$ điểm)

Cho tứ giác $ABCD$ nội tiếp ($O$)

$a)$ Gọi $J$ là giao điểm $AC$ và $BD$. Đường tròn ($O'$) tiếp xúc với hai tia $JA;JB$ tại $E;F$ và tiếp xúc trong với ($O$). Chứng minh đường thẳng $EF$ đi qua tâm đường tròn nội tiếp tam giác $ABD$

$b)$ Các đường phân giác ngoài của các góc tứ giác $ABCD$ cắt nhau tạo thành tứ giác $MNPQ$. Gọi $X;Y$ lần lượt là trung điểm của $MP;NQ$ . Chứng minh rằng $X;O:Y$ thẳng hàng.

 

Câu $4$ ($5,0$ điểm)

Viết các số từ $1$ đến $2015$ lên bảng. Ta chọn hai số bất kì $a;b$ trên bảng và xóa chúng đi. Sau đó viết thêm $|a-b|$ lên bảng. Thực hiện liên tiếp cho đến khi bảng chỉ còn lại một số. Gọi số đó là $m$

$a)$ Số $m$ có thể bằng $1$ hay không ?

$b)$ Tìm tập hợp các giá trị của $m$ .

 

----------------------------Hết----------------------------

Bài viết đã được chỉnh sửa nội dung bởi Quoc Tuan Qbdh: 20-11-2015 - 23:07

[dogsteven]

Bài 1. Bằng AM-GM, ta có thể chứng minh: $2(a+b+c)(a^2+b^2+c^2)\geqslant 3(a^2b+b^2c+c^2a+ab^2+bc^2+ca^2)$

Áp dụng bất đẳng thức Cauchy-Schwarz: $\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\geqslant \dfrac{(a+b+c)^2}{2(ab+bc+ca)}$

Áp dụng bất đẳng thức Holder: $\sum \sqrt{\dfrac{a}{b+c}}\geqslant \sqrt{\dfrac{(a+b+c)^3}{2(a^2b+b^2c+c^2a+ab^2+bc^2+ca^2)}}\geqslant \dfrac{a+b+c}{2}\sqrt{\dfrac{3}{a^2+b^2+c^2}}$

Bằng việc chuẩn hóa $a+b+c=3$, ta đưa về chứng minh: $\dfrac{3}{ab+bc+ca}+\sqrt{\dfrac{3}{a^2+b^2+c^2}}\geqslant 2$

Đến đây ta mạnh dạng áp dụng bất đẳng thức AM-GM: $VT\geqslant 2\sqrt{\dfrac{3\sqrt{3}}{\sqrt{(a^2+b^2+c^2)(ab+bc+ca)^2}}}$

Áp dụng bất đẳng thức AM-GM: $(ab+bc+ca)^2(a^2+b^2+c^2)\leqslant \dfrac{(a+b+c)^6}{27}=27$ nên ta có điều phải chứng minh.

[TonnyMon97]

Câu 4a/ Câu trả lời là không do số cuối cùng không thể là số lẻ.

Thật vậy, theo quy luật đề bài ta có:

chẵn + chẵn = chẵn 

lẻ + lẻ = chẵn

chẵn + lẻ = lẻ + chẵn = lẻ

Trước dấu "=" là xóa đi và sau là số viết vào.

Ta thấy số lẽ luôn mất đi 2 hoặc không mất đi qua cả 3 TH ta xóa tùy ý. Mà ta có 1008 số lẻ nên theo luật bất biến rõ ràng số lẻ không thể còn lại cuối cùng.

[dogsteven]

Bài 4b. Ta sẽ chứng minh $m$ thuộc tập các số chẵn từ $0$ đến $2014$ hay là chứng minh với một số chẵn bất kỳ thuộc $\{0,2,4,...,2014\}$ thì ta luôn tồn tại hữu hạn các thao tác biến đổi sao cho số cuối cùng còn lại là số đã chọn.

Giả sử ta muốn có số $2k$. Ta sẽ thực hiện phép biến đổi với các cặp như sau: $(1,2), (3,4),..., (2k-3, 2k-2), (2k-1, 2k+1), (2k+2, 2k+3),..., (2014,2015)$

Sau khi thực hiện các phép biến đổi sẽ ra $1006$ số $1$, $1$ số $2$ và số $2k$

Ta thực hiện phép biến đổi cho $(2,1)$ thì ta được $1006$ số $1$ và số $2k$

Đến đây thực hiện phép biến đổi cho từng cặp số $1$ thì chỉ còn lại $503$ số $0$ và số $2k$ và đến đây thì áp dụng phép biến đổi tùy ý, đến cuối ta được số $2k$

Vậy ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi dogsteven: 21-11-2015 - 16:43

[Phanbalong]

Câu 1: Chuẩn hóa $a+b+c=3$, khi đó BĐT trở thành:

$\sum (\frac{a}{3-a}+\sqrt{\frac{a}{2(3-a)}})\geq 3$

Lại có: $\frac{a}{3-a}+\sqrt{\frac{a}{2(3-a)}}=\frac{2a+\sqrt{2a(3-a)}}{2(3-a)}\geq \frac{9}{8}a-\frac{1}{8}$

Thiết lập 2 BĐT tương tự rồi cộng lại suy ra ĐPCM

Bạn cho mình hỏi ở đây mình biết  bạn dùng UCT, nhưng mình lại không biết cách mà bạn lại biết đổi ra được $\frac{9}{8}a -\frac{1}{8}$ , cũng như cách bạn chứng minh bất đẳng thức bạn tìm được là đúng  . Mong bạn viết rõ một tí , mình còn hơi kém

[Hoang Nhat Tuan]

Bạn cho mình hỏi ở đây mình biết  bạn dùng UCT, nhưng mình lại không biết cách mà bạn lại biết đổi ra được $\frac{9}{8}a -\frac{1}{8}$ , cũng như cách bạn chứng minh bất đẳng thức bạn tìm được là đúng  . Mong bạn viết rõ một tí , mình còn hơi kém

Mình tính đạo hàm bạn ạ, gọi là phương pháp tiếp tuyến trong chứng minh BĐT  

[longatk08]

Cho $a,b,c$ không âm thỏa $ab+bc+ac+abc=4$.Chứng minh rằng:

 

$$a+b+c+\sqrt{a+b+c+2abc+4} \geq 6$$

 

Bất đẳng thức tương tự sau vẫn đúng:

 

$$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\left(\sqrt{\frac{a}{b+c}}+\sqrt{\frac{c}{a+b}}+\sqrt{\frac{b}{a+c}}\right)^2\geq 6$$

 

$$(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b})\left(\sqrt{\frac{2a}{a+b}}+\sqrt{\frac{2c}{c+a}}+\sqrt{\frac{2b}{b+c}}\right)\geq \frac{9}{2}$$

Bài viết đã được chỉnh sửa nội dung bởi longatk08: 22-11-2015 - 09:06

[Phanbalong]

Mình tính đạo hàm bạn ạ, gọi là phương pháp tiếp tuyến trong chứng minh BĐT

mình lại tưởng là UCT, vậy cho mình hỏi dùng UCT ở đây có được ko vậy ? 

[Hoang Nhat Tuan]

Câu $3$ ($5,0$ điểm)

Cho tứ giác $ABCD$ nội tiếp ($O$)

$a)$ Gọi $J$ là giao điểm $AC$ và $BD$. Đường tròn ($O'$) tiếp xúc với hai tia $JA;JB$ tại $E;F$ và tiếp xúc trong với ($O$). Chứng minh đường thẳng $EF$ đi qua tâm đường tròn nội tiếp tam giác $ABD$

$b)$ Các đường phân giác ngoài của các góc tứ giác $ABCD$ cắt nhau tạo thành tứ giác $MNPQ$. Gọi $X;Y$ lần lượt là trung điểm của $MP;NQ$ . Chứng minh rằng $X;O:Y$ thẳng hàng.

Câu a): Đây chính là định lý Lyness mở rộng.

 

Câu b) Không liên quan đến câu a) lắm (giống định lý Newton).

Bài viết đã được chỉnh sửa nội dung bởi Hoang Nhat Tuan: 22-11-2015 - 17:35

[Nguyen Minh Hai]

Câu số học có vẻ giống bài IMO 1990. 

[Hoang Nhat Tuan]

Câu số học có vẻ giống bài IMO 1990. 

Hơi liên quan: T gọi $p$ là ước nguyên tố nhỏ nhất của $n$ thì chứng minh được $a$ phải là số tự nhiên thỏa mãn $a+1$ chia hết cho $p^2$ (đó mới là điều kiện cần, chưa phải điều kiện đủ).

Nói chung: "Ngu số" @@  

[viet nam in my heart]

 

Câu $3$ ($5,0$ điểm)

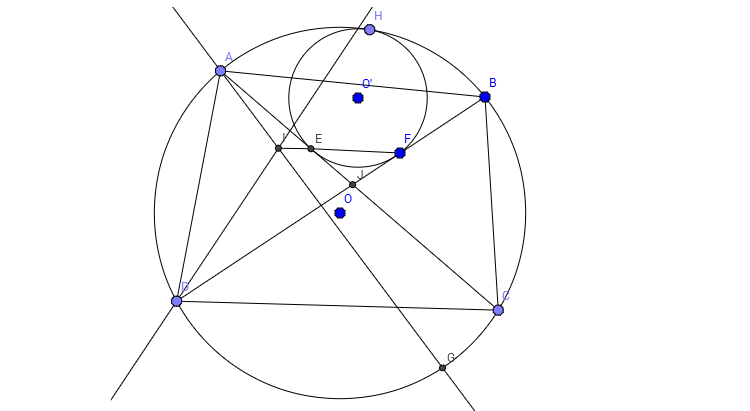
Cho tứ giác $ABCD$ nội tiếp ($O$)

$a)$ Gọi $J$ là giao điểm $AC$ và $BD$. Đường tròn ($O'$) tiếp xúc với hai tia $JA;JB$ tại $E;F$ và tiếp xúc trong với ($O$). Chứng minh đường thẳng $EF$ đi qua tâm đường tròn nội tiếp tam giác $ABD$

$b)$ Các đường phân giác ngoài của các góc tứ giác $ABCD$ cắt nhau tạo thành tứ giác $MNPQ$. Gọi $X;Y$ lần lượt là trung điểm của $MP;NQ$ . Chứng minh rằng $X;O:Y$ thẳng hàng.

 

 

Câu $3$ ($5,0$ điểm)

Cho tứ giác $ABCD$ nội tiếp ($O$)

$a)$ Gọi $J$ là giao điểm $AC$ và $BD$. Đường tròn ($O'$) tiếp xúc với hai tia $JA;JB$ tại $E;F$ và tiếp xúc trong với ($O$). Chứng minh đường thẳng $EF$ đi qua tâm đường tròn nội tiếp tam giác $ABD$

$b)$ Các đường phân giác ngoài của các góc tứ giác $ABCD$ cắt nhau tạo thành tứ giác $MNPQ$. Gọi $X;Y$ lần lượt là trung điểm của $MP;NQ$ . Chứng minh rằng $X;O:Y$ thẳng hàng.

Câu a): Đây chính là định lý Lyness mở rộng.

Câu b) Không liên quan đến câu a) lắm (giống định lý Newton).

 

Câu hình b) (Câu a là Bổ đề $Sawayama$)

Bổ để 1: $MP \perp NQ$

Gọi $X$ là giao điểm của $AD$ và $BC$. $Y$ là giao điểm của $AB$ và $CD$

Theo giả thiết dễ dàng suy ra $M,N$ lần lượt là tâm đường tròn nội tiếp $2$ tam giác $YAD$ và $XAB$

                                                $P$ là tâm đường tròn bàng tiếp trong góc $Y$ của tam giác $YBC$

                                                $Q$ là tâm đường tròn bàng tiếp trong góc $X$ của tam giác $XCD$

Do đó: $X,N,Q$ thẳng hàng và $Y,M,P$ thẳng hàng. $YP$ và $XQ$ lần lượt là phân giác góc $\widehat{BYC}$ và góc $\widehat{DXC}$

Gọi $Z$ là giao điểm của $YP$ và $XQ$ ta có: $$\widehat{XZY}=180^o -\left(\widehat{AYX}+\widehat{AXY}\right)-\widehat{ZYA}-\widehat{ZXA} =\widehat{XAY}-\dfrac{\widehat{BYC}+\widehat{DXC}}{2}$$

Lại có: $\widehat{XAY}-\dfrac{\widehat{BYC}+\widehat{DXC}}{2}=\widehat{BAD}-\dfrac{\left(180^o-\widehat{ABC}-\widehat{BCD}\right)+\left(180^o-\widehat{CDA}-\widehat{BCD}\right)}{2}=90^o$

Vậy $MP \perp NQ$

Bổ đề 2: Gọi $E,F,G,H$ lần lượt là giao điểm thứ hai của $\left(O\right)$ với $MN,NP,PQ,QM$. Khi đó $EF \parallel GH \parallel MP,EH \parallel FG \parallel NQ$ và $EFGH$ là hình chữ nhật

Ta có: $\widehat{EMP}=\widehat{YAM}+\widehat{AYM}=\dfrac{\widehat{YAD}+\widehat{AYD}}{2}=\dfrac{\widehat{ADC}}{2}$

Lại có: $\widehat{NEF}=\widehat{NBA}=\dfrac{\widehat{XBA}}{2}=\dfrac{\widehat{ADC}}{2}=\widehat{EMP}$

Suy ra $EF \parallel MP$

Chứng minh tương tự ta thu được: $EF \parallel GH \parallel MP,EH \parallel FG \parallel NQ$

Kết hợp với bổ đề $1$ suy ra điểu phải chứng minh

Trở lại bài toán: Gọi $I,J$ lần lượt là trung điểm của $MP,NQ$. Ta cần chứng minh $O,I,J$ thẳng hàng

Gọi $K$ là trung điểm của $EH$. $I'$ là giao điểm của $OJ$ với $MP$. Ta sẽ chứng minh $I \equiv I'$ hay $I'$ là trung điểm của $MP$

Vì $EH \parallel NQ$ nên $M,K,J$ thẳng hàng.

Vì $K$ là trung điểm của $EH$ nên $OK \perp EH$. Mà $EH \perp MP$ nên $OK \parallel MP$

Vì $EFGH$ là hình chữ nhật nên $O$ là đồng thời là trung điểm của $EG$ và $FH$. Suy ra $HG=EF=2OK$

Áp dụng định lý $Thales$ ta có: $$\dfrac{OK}{MI'}=\dfrac{JK}{JM}=\dfrac{QH}{QM}=\dfrac{HG}{MP}=\dfrac{2OK}{MP}$$

Suy ra $MP= 2MI'$ hay $I'$ là trung điểm của $MP$. Suy ra $I \equiv I'$ hay $O,I,J$ thẳng hàng

Vậy $O,I,J$ thẳng hàng

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 31-03-2017 - 11:25