Việc xác định chúng ta còn lại bao nhiêu thời gian trước khi tiếp cận một zombie chính là sự khác biệt giữa người sống, kẻ chết và zombie. Ở đây giả sử chúng ta mô hình một lượng zombie rải rác ngẫu nhiên trên miền một chiều. Nhờ vào mô hình này, chúng ta có thể dự đoán được số lần chạm trán với zombie chính xác (hoặc gần đúng), điều này cho ta phương pháp tốt nhất để né tránh cuộc gặp không mấy tốt lành này.

Zombie trong tác phẩm "Đêm của xác sống" của George Romero
I. GIỚI THIỆU
Con người không thể sống sót cũng như làm việc trong một không gian mà zombie gần như chiếm kín nơi đó. Bởi vì, thực tế cho thấy bọn zombie được kết hợp bởi hai nhân tố đầy chết chóc chính là sự bất tử (cho tới khi não chúng bị hủy) và sự thẻm khát thịt tươi tột độ.
Tuy nhiên, công việc này đã được giải quyết bởi Philip Munz và cộng sự. Ông giả định rằng zombie và người cùng “trộn”, có nghĩa là ta có thể tìm thấy zombie ở mọi nơi và con người cũng vậy. Thực tế những nhóm zombie ban đầu sẽ tập hợp tại các khu vực nhiều người chết, ví dụ như ở các nghĩa trang hay bệnh viện. ngoài ra con người không thể bảo toàn mạng khi chỉ chạy và trốn nếu ban đầu không tách hẳn người và zombie ra hai khu vực. Thêm một điều kiện nữa chính là zombie di chuyển khá chậm so với người, do đó, từ xa con người có thể thấy được nguy hiểm đang tiến đến gần và chạy nhanh hơn zombie từ đó tiến đến việc thiết lập một hàng rào phòng hộ giúp ngăn cách con người và zombie. Để thực hiện được điều này, chúng ta cần phải nắm rõ chúng ta có bao nhiêu thời gian để giữ vững rào chắn trước một đợt zombie vì điều này sẽ cho chúng ta một số ước tính như “chúng tôi có bao lâu để thu dọn vật tư?”, “có bao lâu để trang bị lại vũ khí?”, ”có khả thi khi bảo vệ những người đang tới?”.
Nếu người đọc có quá ít thời gian để hiểu rõ nội dung toán học trước khi tận thế, tôi khuyên bạn nên bỏ qua lý luận toán học và tiến thẳng đến một số kết quả có ích dưới đây.
II.ĐƯỜNG ĐI NGẪU NHIÊN VÀ SỰ KHUẾCH TÁN
Theo Munz, “xác sống di chuyển với bước đi nhỏ, hướng đi không rõ ràng”, điều này làm cho chuyển đông của một phần tử trong mô hình này chính là một bước ngẫu nhiên. “Kẻ say rượu” hay bước ngẫu nhiên là khái niệm nhằm mô tả các chuyển động không xác định rõ hướng. Để đưa ra ý tưởng trực quan về bước ngẫu nhiên, chúng ta liên tưởng đến hình ảnh kẻ say rượu bước đi loạng choạng không định hướng. Trong hình ta minh họa chuyển động này với zombie, chúng sẽ di chuyển ngẫu nhiên xung quanh cho đến khi chạm vào một thứ gì đó khiến chúng đổi hướng, do đó chúng sẽ trải rộng ra trên miền xác định. Sự khuếch tán có hai đặc điểm cơ bản đó là tính ngẫu nhiên trong tự nhiên và tính di chuyển từ nơi có mật độ cao về nơi có mật độ thấp.
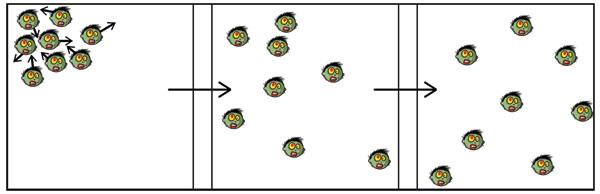
Hình 1 là một ví dụ cho ta thấy về sự khuếch tán hai chiều trên một nhóm ban đầu, hướng đi ban đầu đươc thể hiện bởi các mũi tên màu đen. Sau một thời gian chuyển động ngẫu nhiên, chúng ta được miền như hình.
Chúng ta có thể mô hình lại chuyển động của mỗi zombie riêng lẻ nhưng vì sự di chuyển của chúng là ngẫu nhiên (trừ khi chúng ta theo dõi chúng một cách chính xác) nên ta không thể chắc chắn vị trí của chúng. Cách mô tả theo xác suất cũng có thể được sử dụng tuy nhiên do số lượng zombie quá lớn nên khả năng tính toán đến một số lượng nào đó sẽ sớm mất đi hiệu quả cần thiết cho dù ta không có chạy trốn. Thay vào đó, chúng ta xem xét trường hợp có một số lượng lớn hữu hạn zombie, điều này tạo ra một mô hình khuếch tán liên tục, dễ sử dụng hơn, cần ít tính toán hơn và phương pháp phân tích đều đã có sẵn. Tuy nhiên, phương pháp này có độ chính xác ít hơn. Thực tế, mật độ zombie trong từng khu vực là một số nguyên rời rạc, ví dụ như $1~zombie/m$ ,$4~zombie/m$, … (giả sử zombie bị cụt tay, chân vẫn được tính là 1 con) Tuy nhiên, thông qua giả định khuếch tán trên một số lượng rất lớn zombie nào đó, ta buộc phải cho phép giá trị mật độ có thể nhận bất kỳ giá trị nào, kể cả số không nguyên. Vì thế mật độ thay vì là một giá trị của hàm rời rạc thì nó đã được “trơn hóa” để tạo thành một hàm liên tục.
III. MÔ TẢ TOÁN HỌC CHO SỰ KHUẾCH TÁN
Nhằm đơn giản hóa vấn đề này, chúng ta sẽ khảo sát trên không gian 1 chiều (kí hiệu $x$) nghĩa là chúng ta chỉ làm việc trên một đường thẳng. Điều này hầu như không dẫn đến hạn chế các kết quả có thể đúng trong không gian 2 chiều hoặc thậm chí là 3 chiều. Nói cách khác, giả thiết này có nghĩa là chỉ tồn tại một điểm có thể tiếp cận tới hàng phòng thủ của chúng ta, đồng thời khoảng cách ngắn nhất giữa zombie và người chính là đường thẳng.
Nếu chúng ta cho mật độ zombie tại thời điểm $t$ bằng $x$ là một bộ $Z\left( x,t \right)$ thì $Z$ phải thỏa mãn phương trình khuếch tán:
$$\frac{\partial Z}{\partial t}\left( x,t \right)=D\frac{{{\partial }^{2}}Z}{\partial {{x}^{2}}}~~\left( 1 \right)$$
Giá trị $\frac{\partial Z}{\partial t~}\left( x,t \right)$ mô tả tốc độ thay đổi của $Z$ theo thời gian tại vị trí $x$. Điều này nghĩa là nếu $\frac{\partial Z}{\partial t}>0$ thì $Z$ đang tăng tại vị trí $x$ và thời điểm $t$. Giá trị này cho phép chúng ta xác định được $Z\left( x,t \right)$ phát triển thế nào theo thời gian.
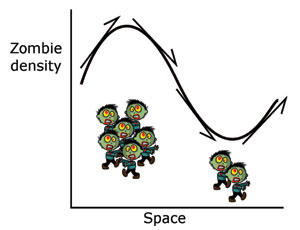
Hình 2. Một ví dụ cho thấy cách khuếch tán làm trơn vị trí cực đại và cực tiểu
Phần tử $D$ là hằng số dương qui định tốc độ di chuyển. Đơn vị của $D$ được chọn sao cho phương trình khuếch tán không bị mẫu thuẫn. Các giá trị $\partial Z/\partial t$ có đơn vị [mật độ]/[thời gian] và giá trị ${{\partial }^{2}}Z/\partial {{x}^{2}}$ có đơn vị [mật độ]/[diện tích]2, như vậy $D$ phải có đơn vị là [diện tích]2/[thời gian]. Các đơn vị có thể ở dạng $k{{m}^{2}}/h$ hoặc $n{{m}^{2}}/s$. Tuy nhiên, để phương trình có nhiều thông tin nhất, ta chọn thang đo tương ứng với cuộc xâm lược của zombie, do đó chúng ta chọn đơn vị là ${{m}^{2}}/ph$ ($ph$ là viết tắt của phút).
Ta thấy vế phải của phương trình (1) có một chút phức tạp hơn so với vế trái, nhưng về cơ bản nó tóm lược ý tưởng rằng các zombie đang di chuyển từ nơi có mật độ cao về nơi có mật độ (được mô tả lại trong hình 2). Ban đầu có nhiều zombie ở bên trái hơn bên phải, điều này có nghĩa là trước khi đạt đỉnh, mũi tên (là tiếp tuyến của đường cong, hay $\partial Z/\partial x$ tại điểm $x$) chỉ hướng lên. Điều này có nghĩa là khi $x$ tăng thì khi đó mật độ zombie $Z$ cũng tăng. Tại điểm này:
$$\frac{\partial Z}{\partial x}=\text{tốc độ thay đổi của }Z\text{ khi }x\text{ tăng }>0$$
Và sau khi qua đỉnh, tiếp tuyến hướng xuống, khi đó:
$$\frac{\partial Z}{\partial x}=\text{tốc độ thay đổi của }Z\text{ khi }x\text{ tăng }<0$$
Do đó, tại đỉnh, $\partial Z/\partial x$ giảm khi $x$ tăng (vì di chuyển từ nơi dương đến nơi âm). Vì ${{\partial }^{2}}Z/\partial {{x}^{2}}$ là tốc độ thay đổi của $\partial Z/\partial x$ khi $x$ tăng và ta vừa suy luận rằng $\partial Z/\partial x$ đang giảm tại đỉnh nên:
$$\frac{{{\partial }^{2}}Z}{\partial {{x}^{2}}}<0$$
Theo phương trình khuếch tán, tại đỉnh:
$$\frac{\partial Z}{\partial t}=D\frac{{{\partial }^{2}}Z}{\partial {{x}^{2}}}<0$$
Điều này có nghĩa là tại điểm cực đại, mật độ zombie giảm theo thời gian. Tương tự, $\partial Z/\partial x<0$ trước khi đạt cực tiểu và $\partial Z/\partial x>0$ sau khi đạt cực tiểu như minh họa trong hình 2. Như vậy, khi đạt cực tiểu, ${{\partial }^{2}}Z/\partial {{x}^{2}}>0$ thể hiện mật độ đang tăng. Nhìn chung, sự khuếch tán khiến cho zombie di chuyển trong miền từ nơi có mật độ cao về nơi có mật độ thấp.
Ta không thể nói quá về tính quan trọng của phương trình (1). Ở bất kỳ đâu , khi ta mô tả tính ngẫu nhiên và không rõ hướng của vật thể di chuyển trong mô hình, ta sẽ xác định phương trình khuếch tán. Điều này có nghĩa rằng khi am hiểu về phương trình khuếch tán, ta có thể miêu tả nhiều hệ khác nhau như tính dẫn nhiệt qua vật thể rắn, khí gas tỏa khắp phòng, chất đạm di chuyển khắp cơ thể, di chuyển phân tử trong phản ứng hóa học, nước mưa rỉ xuống lòng đất, tính tương tác của động vật ăn thịt con mồi.
IV.LỜI GIẢI CHO PHƯƠNG TRÌNH KHUẾCH TÁN
Phương trình khuếch tán cho ta một mô tả toán học rõ ràng về sự di chuyển của zombie. Bằng việc giải phương trình này, chúng ta có được giá trị $Z\left( x,t \right)$, mật độ zombie tại từng vị trí $x$ với mọi thời gian $t~\ge ~0$. Tuy nhiên, ta vẫn cần thêm một số dữ kiện để giải phương trình này.
Ban đầu, ta có mật độ ${{Z}_{0}}~zombie/m$. Giả sử tất cả zombie đều bắt đầu từ một khoảng $0\le x\le 1$. Nghĩa là tất cả xác sống đều bắt nguồn từ một nơi xác định như nghĩa trang hay nhà xác bệnh viện.
Giả thiết cuối cùng đặt ra chính là zombie không thể di chuyển ra khỏi vùng $0\le x\le L$. Nghĩa là có một ranh giới tại $x=0$ mà zombie không thể vượt qua, nếu zombie vượt qua các giới hạn này thì sẽ bị tung lên và phản xạ lại. Và việc ta cần làm chính là đặt các chốt canh phòng tại $x=L$ . Như vậy, tại điểm $x=0$ và $x=L$ “lưu lượng zombie”(tốc độ thay đổi của zombie qua ranh giới) là 0. Có nhiều điều kiện để xây dựng nhiều ranh giới khác nhau, tuy nhiên để đơn giản, ta chọn ranh giới tại $x=0$ để ngăn chặn zombie rời khỏi khu vực đang xét nhưng không làm thay đổi số lượng zombie.
Về mặt toán học, lưu lượng zombie qua $x=0$ và $x=L$ là không gian đạo hàm tại những khoảng khác nhau và vì ta giả định kết quả là 0 thì $\partial Z/\partial x=0$ tại $x=0$ hoăc $x=L$.
Hệ được mô tả đầy đủ như sau:
$$\frac{\partial Z}{\partial x}\left( x,t \right)=D\frac{{{\partial }^{2}}Z}{\partial {{x}^{2}}}\left( x,t \right),$$
với các điều kiện ban đầu:
$$Z(x,0)=\left\{\begin{matrix} Z_{0}\: \text{với }0\leq x\leq 1\\ 0 \: \text{với }x> \end{matrix}\right.$$
và điều kiện biên:
$$\frac{\partial Z}{\partial x}\left( 0,t \right)=0=\frac{\partial Z}{\partial x}\left( L,t \right)$$
Với hệ này, cùng với điều kiện ban đầu và điều kiện biên, ta có thể giải được chính xác, có dạng:
$$Z\left( x,t \right)=\frac{{{Z}_{0}}}{L}+\underset{n=1}{\overset{\infty }{\mathop \sum }}\,\frac{2{{Z}_{0}}}{n\pi }\sin \left( \frac{n\pi }{L} \right)cos\left( \frac{n\pi }{L}x \right)\exp \left( -{{\left( \frac{n\pi }{L} \right)}^{2}}Dt \right)$$
Các hàm số $\sin ~$ và $\cos ~$ là những hàm số lượng giác và hàm mũ $\exp ~$ là một trong những toán tử cơ bản trong toán học, ta sử dụng tính chất của các hàm trên khi $a>0$, lúc đó $\exp \left( -at \right)\to 0$ khi $t\to \infty $. Xem đây là nghiệm và áp vào hệ, khi đó $t$ tiến đến vô cùng lớn nên vế phải của phương trình tiến dần đến giá trị rất nhỏ, xấp xỉ 0. Do đó, với giá trị $t$ rất lớn nào đó, ta có thể tính gần đúng
$$Z\left( x,t \right)\approx \frac{{{Z}_{0}}}{L}$$
Điều này có nghĩa là khi thời gian tăng lên thì zombie càng lan rộng ra với mật độ trung bình là ${{Z}_{0}}/L$ tại mọi vị trí.
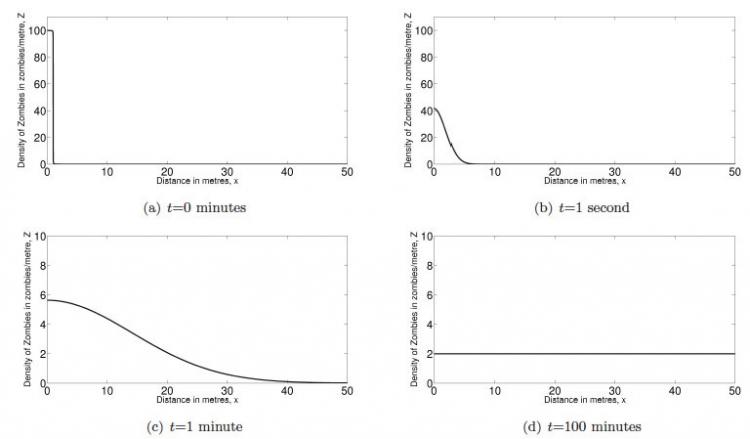
Trong hình 3, ta đánh dấu mật độ zombie tại một số vị trí, tại hình 3(a) cho thấy điều kiện ban đầu của mật độ lớn zombie giữa $0\le x\le 1$. Hình 3(b) và 3(c) mô tả cách để sự khuếch tán dẫn dến mật độ cực đại xuất hiện lần đầu tiên tại một vị trí và sau đó lan ra các miền xung quanh. Để ý rằng ta đã thay đổi tỉ lệ của các trục trong hình 3(c) và 3(d) để minh họa lời giải rõ ràng hơn. Hình 3(d) làm rõ kết quả xấp xỉ khi $t$ vô cùng lớn, vì sau 100 phút mật độ zombie đã trở nên đồng nhất trên toàn miền.
Hình 3. Sự phát triển của một nhóm zombie trong khoảng thời gian 100 phút. Những zombie được giả định trong một miền dài 50m và có hệ số khuếch tán là $D=100{{m}^{2}}/ph\acute{u}$.
V. THỜI ĐIỂM ĐẦU TIÊN TIẾP CẬN ZOMBIE
Kết quả cho chúng ta mật độ zombie tại mọi vị trí $x$ và tại mọi thời điểm $t$. Có rất nhiều vấn đề có thể giải quyết thông qua nghiệm của phương trình này. Tuy nhiên, vấn đề được những người sống sót nhấn mạnh ở đây chính là ”chúng ta có bao nhiêu thời gian trước khi zombie đầu tiên đến đây?” và mô hình toán học của câu hỏi trên là “với thời điểm ${{t}_{z}}$ nào thì $Z\left( L,{{t}_{z}} \right)=1$?”, trong đó ${{t}_{z}}$ là khoảng thời gian di chuyển (trung bình) mà zombie mất để đạt đến vị trí $x=L$.
Thật không may là chúng ta không thể có một cách giải chính xác trong thời điểm này. Tuy nhiên, có một phương pháp (mà chúng ta không đề cập ở đây) có thể tính xấp xỉ kết quả với độ chính xác mà chúng ta mong muốn.
Sử dụng phương pháp này, chúng ta có thể thay đổi khoảng cách và tốc độ của zombie để tính toán thời gian tiếp cận khác nhau. Trong hình 4 chúng ta mô phỏng thời gian tiếp cận của một nhóm zombie với tốc độ khuếch tán ban đầu là $100{{m}^{2}}/ph$ đến $150{{m}^{2}}/ph$, tốc độ này hợp lý trong thực tế ứng với chuyển động lê bước chậm trong khoảng từ 50 đến 90m. Để ý rằng với khoảng cách lớn hơn $L=100m$ mật độ trung bình sẽ ít hơn $1~zombie/m$ nên ta không có nghiệm ${{t}_{z}}$ sao cho $Z\left( L,{{t}_{z}} \right)=1$ vì $Z\left( L,t \right)<1$ với mọi $t\ge 0$. Trong trường hợp này, giả định rằng có một số lượng lớn zombie đã chết sẽ khiến cho mô hình liên tục này không còn phù hợp nữa.
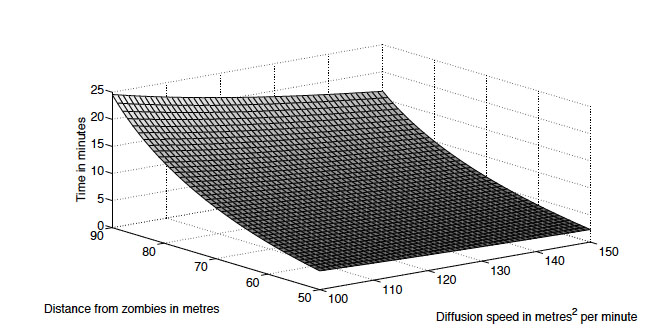
Hình 4. Phân bố thời gian (tính bằng phút) cho đến khi mật độ zombie tiến đến 1 với tốc độ khuếch tán và khoảng cách khác nhau
Phương án xấp xỉ của chúng ta cũng trả lời một câu hỏi quan trọng: chúng ta có nên trì hoãn thời gian tiếp cận zombie lại bằng cách chạy xa hơn, hoặc làm zombie đi chậm lại? Theo đồ thị trên cho thấy, khi so sánh với giảm tốc độ khuếch tán của zombie thì tăng khoảng cách giữa chúng ta và zombie sẽ dẫn đến tăng khoảng thời gian tiếp cận $t$ lớn hơn.
Vì chúng ta muốn trì hoãn thời gian tiếp cận zombie càng lâu càng tốt, ta thấy rằng sẽ lợi thế hơn nếu ta tốn năng lượng để tránh xa khỏi các zombie hơn là cố gắng cản chân chúng mà không có một vũ khí tầm xa hay một chiếc cưa máy, và hiển nhiên việc giết chết một zombie là rất khó khăn nếu như chúng ta chưa phá hủy được bộ não của chúng.
Ta nên lưu ý rằng thời gian chúng ta tính được qua phương pháp này luôn ngắn hơn so với thực tế. Trong thực tế, zombie lan rộng ra trên cả hai hướng và chúng gặp các trở ngại bởi các vật cản cũng như các nạn nhân nằm trên đường, vì vậy thời gian zombie tiếp cận chúng ta có thể lâu hơn so với dự kiến. Ước tính của chúng ta có phần quá thận trọng mặc dù điều này sẽ giữ chúng ta an toàn vỉ tác giả bài viết muốn rời khỏi mốt đe dọa chứ không muốn thêm một vài phút chỉ để lụm lặt gì đó!
VI. KẾT LUẬN
Mô hình khuếch tán cho biết ta còn bao lâu nữa trước khi zombie đến. Hơn nữa toán học còn có thể tìm ra phương pháp làm chậm quá trình lây nhiễm của zombie hoặc thậm chí có thể trả lời câu hỏi: “Liệu tất cả có thể sống sót?”. (Nếu bạn cảm thấy thích thú về chủ đề này, có thể bạn sẽ thích cuốn Mathematical Modelling of Zombies.)
Đối với những người còn trong vòng vây của xác sống, ta có thể tóm tắt kết quả lại rằng chạy trốn là một chiến lược thành công hơn hẳn so với việc cố gắng làm chậm bước tiến của zombie. Do đó muốn tồn tại được bạn nhất định phải cố gắng bỏ chạy khi bạn có cơ hội.
Tuy nhiên chúng ta không thể chạy mãi được, bắt gặp zombie là điều không thể tránh khỏi. Do đó về mặt toán học, chúng ta nên xây dựng một cộng đồng vững chắc, có thể duy trì được dân số con người cũng như có thể loại bỏ được zombie khi chúng tiếp cận. Tuy nhiên, nếu các biện pháp bảo vệ thất bại hoạc bạn không tìm được một nhóm cộng đồng như vậy thì rõ ràng tính khả thi của cách này không cao.
Có vẻ như chúng ta đã đi đến một kết luận thật nghiệt ngã, chúng ta không hề muốn vậy nhưng sự thật là như vậy. Cách duy nhất để có thể tồn tại đó là chúng ta phải chạy, chạy đến nơi xa nhất có thể (một hòn đảo có thể là một lựa chọn không tồi). Bạn chỉ nên chống lại nếu bạn chắc chắn chiến thắng đã trong tầm tay và tìm những người có thể giúp bạn sống sót.
Chúc may mắn. Bạn sẽ cần đến nó!
Nguồn: https://plus.maths.o...-can-we-survive
Người dịch: Nguyễn Văn Sáng Hồng, thành viên Chuyên san EXP dịch