Chủ đề này có 63 trả lời

[NTA1907]

ĐỀ THI SỐ 8 : 
Bài 3 : Cho $a,b,c$ là các số thực dương có tổng bằng $2016$. Chứng minh : 
$\sum \frac{a^2+bc}{b+c} \ge 2016$ 

Ta chứng minh:

$\sum \frac{a^{2}+bc}{b+c}\geq \sum a$

$\Leftrightarrow \sum \frac{a^{2}+bc+ab+ac}{b+c}\geq 2\sum a$

$\Leftrightarrow \sum \frac{(a+b)(a+c)}{b+c}\geq 2\sum a$

Đặt $a+b=x, b+c=y, c+a=z\Rightarrow 2\sum a=x+y+z$

Ta chỉ cần cm: $\sum \frac{xy}{z}\geq \sum x$

$\Leftrightarrow x^{2}y^{2}+y^{2}z^{2}+z^{2}x^{2}\geq xyz(x+y+z)$(đúng theo AM-GM)

$\Rightarrow$ đpcm

[tpdtthltvp]

                                                                  ĐỀ THI SỐ 8 : 
Bài 1: (1,5 điểm) Cho các số thực dương $x,y,z$ thỏa mãn : 
$\begin{cases} &x^2+y^2=9&\\&y^2+z^2=16&\\&y^2=xz& \end{cases}$ 
Tính giá trị của $A=xy+yz$
 

Bài 2: Tìm nghiệm nguyên của các phương trình sau : 
     a) $x^2+2y^2+2xy+3y-4=0$ 
     b) $x^4+x^2-y^2+y+10=0$ 
 

Bài 4: Tìm số lớn nhất trong ba số dương $x,y,z$ thỏa mãn hệ phương trình : 
$\begin{cases} &x=1-|1-2y|&\\&y=1-|1-2z|&\\&z=1-|1-2x|& \end{cases}$ 
 

Bài 1:

$\begin{cases} &x^2+y^2=9&\\&y^2+z^2=16&\\&y^2=xz& \end{cases}\Rightarrow \left\{\begin{matrix} x^2+2y^2+z^2=25 & & \\ y^2=xz & & \end{matrix}\right.\Rightarrow \left\{\begin{matrix} (x+z)^2-2xz+2y^2=25 & & \\ y^2=xz & & \end{matrix}\right.\Rightarrow (x+z)^2=25$

$\Rightarrow x+z=5$ hoặc $x+z=-5$.

Mà từ $2$ PT đầu $\Rightarrow (z-x)(z+x)=7$

Từ đó tìm được $x,z$ rồi tìm được $y$.

 

Bài 2:

a) $x^2+2y^2+2xy+3y-4=0\Rightarrow x^2+2y.x+(2y^2+3y-4)=0\Rightarrow \Delta _x=(2y)^2-4(2y^2+3y-4)\geq 0\Leftrightarrow -4y^2-12y+16\geq 0\Leftrightarrow (y-1)(y+4)\leq 0\Leftrightarrow -4\leq y\leq 1y\in \left \{ -4;-3;-2;-1;0;1 \right \}$

Tới đây xét từng giá trị của $y$ để tìm $x$.

b) Đặt $x^2=a$ ta được PT: $a^2+a-y^2+y+10=0$

Tới đây giải tương tự như trên.

 

Bài 4:

Giả sử $x\geq y\geq z> 0$. Xét các TH:

$+)0<z\leq y\leq x\leq \frac{1}{2}$

$\Rightarrow \left\{\begin{matrix} x=2y & & & \\ y=2z & & & \\ z=2x & & & \end{matrix}\right.\Rightarrow x=y=z=0(L)$

$+)0<z\leq y\leq \frac{1}{2}\leq x$

$\Rightarrow \left\{\begin{matrix} x=2y \\ y=2-2z \\ z=2-2x \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=\frac{8}{9} \\ y=\frac{4}{9} \\ z=\frac{2}{7} \end{matrix}\right.$

$+)0<z\leq \frac{1}{2}\leq y\leq x$

$\Rightarrow \left\{\begin{matrix} x=2-2y \\ y=2z \\ z=2-2x \end{matrix}\right.\Rightarrow \left\{\begin{matrix} x=\frac{6}{7} \\ y=\frac{4}{7} \\ z=\frac{2}{7} \end{matrix}\right.$

$+)0<\frac{1}{2}\leq z\leq y\leq x$

$\Rightarrow \left\{\begin{matrix} x=2-2y \\ y=2-2z \\ z=2-2x \end{matrix}\right.\Rightarrow x=y=z=\frac{2}{3}$

Vậy số lớn nhất là $\frac{8}{9}$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 27-03-2016 - 17:00

[I Love MC]

Bài 1:

$\begin{cases} &x^2+y^2=9&\\&y^2+z^2=16&\\&y^2=xz& \end{cases}\Rightarrow \left\{\begin{matrix} x^2+2y^2+z^2=25 & & \\ y^2=xz & & \end{matrix}\right.\Rightarrow \left\{\begin{matrix} (x+z)^2-2xz+2y^2=25 & & \\ y^2=xz & & \end{matrix}\right.\Rightarrow (x+z)^2=25$

$\Rightarrow x+z=5$ hoặc $x+z=-5$.

Mà từ $2$ PT đầu $\Rightarrow (z-x)(z+x)=7$

Từ đó tìm được $x,z$ rồi tìm được $y$.

Bài 2:

a) $x^2+2y^2+2xy+3y-4=0\Rightarrow x^2+2y.x+(2y^2+3y-4)=0\Rightarrow \Delta _x=(2y)^2-4(2y^2+3y-4)\geq 0\Leftrightarrow -4y^2-12y+16\geq 0\Leftrightarrow (y-1)(y+4)\leq 0\Leftrightarrow -4\leq y\leq 1y\in \left \{ -4;-3;-2;-1;0;1 \right \}$

Tới đây xét từng giá trị của $y$ để tìm $x$.

 

Anh nhận xét : 
Câu 1 : Trong một số trường hợp như thế thì em có thể giải bằng cách em . Tuy vậy em đã đặt thử câu hỏi vì sao đề lại cho $x,y,z$ chưa ? Về cái này phần sau anh sẽ nói 
Câu 2 : Anh nghĩ ngoài cách xét này em có thể dùng phương pháp khác (nếu dùng phương pháp này mà họ cho số to cái là thôi rồi )

[tpdtthltvp]

                                                                  ĐỀ THI SỐ 8 : 

 

Bài 3: Cho $a,b,c$ là các số thực dương có tổng bằng $2016$. Chứng minh : 

$\sum \frac{a^2+bc}{b+c} \ge 2016$ 

 

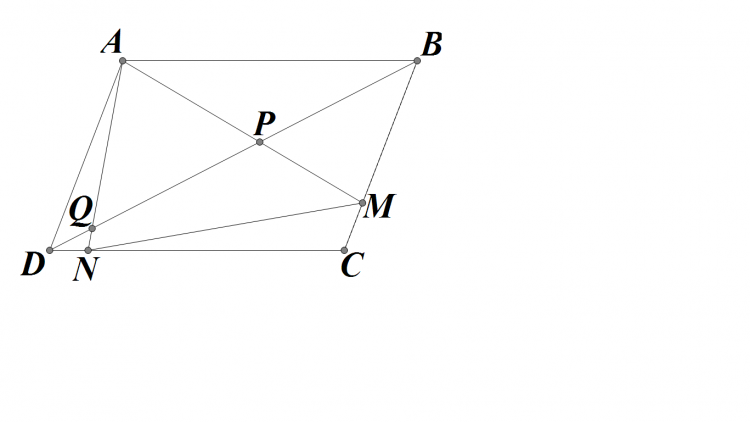
Bài 5: Cho hình bình hành $ABCD$ . Trên các cạnh $BC,CD$ lần lượt lấy $M,N$ sao cho $\frac{BM}{CM}=\frac{CN}{2.DN}=k$. Gọi $P,Q$ theo thứ tự là giao điểm của $AM,AN$ với $BD$. 
a) Chứng minh : $S_{PMNQ}=S_{APQ}$ 
b) Tính $\frac{S_{AMN}}{S_{ABCD}}$ theo $k$ 
 

Bài 6: Có tồn tại hay không $2016$  số nguyên dương $a_1,a_2,..,a_{2016}$ để : 
$a_1^2+a_2^2,a_1^2+a_2^2+a_3^2,...,a_1^2+a_2^2+..+a_{2016}^2$ đều là số chính phương.

Hôm nay rảnh nên "nổi hứng" làm lại mấy bài cũ! Coi như cũng để kết thúc $\boxed{TOPIC}$ luôn, cảm ơn sự đóng góp của mọi người! 

Bài 3:

Ta sẽ chứng minh:

$$\sum \frac{a^2+bc}{b+c}\geq \sum a$$

$$\Leftrightarrow \sum (\frac{a^2+bc}{b+c}-a)\geq 0$$

$$\Leftrightarrow \sum \frac{(a-b)(a-c)}{b+c}\geq 0(1)$$

Đặt $\frac{1}{b+c}=x,\frac{1}{c+a}=y,\frac{1}{a+b}=z$ thì:

$$(1)\Leftrightarrow x(a-b)(a-c)+y(b-c)(b-a)+z(c-a)(c-b)\geq 0(2)$$

Giả sử $a\geq b\geq c$ thì $x\geq y\geq z$. Do đó, $(2)$ đúng theo BĐT $Schur$ suy rộng.

Ta có đpcm. Dấu $"="$ xảy ra khi $a=b=c=672$.

 

Bài 6:

Tồn tại $2016$ số nguyên dương thỏa mãn đề bài. Thật vậy, ta có đẳng thức sau:

$$(2a+1)^2+(2a^2+2a)^2=(2a^2+2a+1)^2$$

Cho $a=1$ thì $a_1=3, a_2=4$ ta được:

$$a_1^2+a_2^2=(2a^2+2a+1)^2=5^2$$

Chọn $a_3=2(a^2+a)^2+2(a^2+a)=12$ ta được:

$$a_1^2+a_2^2+a_3^2=\left [ 2(a^2+a)^2+2(a^2+a)+1 \right ]^2=13^2$$

Tương tự như vậy, ta tìm được $2016$ số thỏa mãn.

 

Bài 5:

a) Ta có: 

$\frac{AP}{PM}=\frac{AD}{BM}=\frac{BC}{BM}=\frac{k+1}{k}\Rightarrow \frac{AP}{AM}=\frac{k+1}{2k+1}$

Và $\frac{AQ}{QN}=\frac{AB}{DN}=\frac{CD}{DN}=2k+1\Rightarrow \frac{AQ}{AN}=\frac{2k+1}{2k+2}$

Do đó:  $S_{APQ}=\frac{AP}{AM}.\frac{AQ}{AN}.S_{AMN}=\frac{1}{2}S_{AMN}$

Vậy ta có $\text{đpcm}$

b) 

$S_{AMB}=\frac{BM}{BC}.S_{ABC}=\frac{k}{k+1}S_{ABC}=\frac{k}{2k+2}S_{ABCD}$

Và: $S_{AND}=\frac{DN}{CD}S_{ACD}=\frac{1}{2k+1}S_{ACD}=\frac{1}{4k+2}S_{ABCD}$

Do đó:

$\frac{S_{AMN}}{S_{ABCD}}=1-(\frac{k}{2k+2}+\frac{1}{4k+2})=\frac{2k^2+4k+1}{4k^2+6k+2}$

Bài viết đã được chỉnh sửa nội dung bởi tpdtthltvp: 01-06-2016 - 10:41