Serbia National Olympiad 2016
Ngày 1.
Bài 1. Cho $n > 1$ là một số nguyên. Chứng minh rằng tồn tại số nguyên $m > n^{n}$ sao cho $\frac{n^{m} - m^{n}}{m + n}$ là số nguyên dương.
Bài 2. Cho $n$ là một số nguyên dương và $f:\mathbb{N}\times \mathbb{N} \to \mathbb{N}$ thỏa mãn các điều kiện sau:
- $f(0, i) = f(i, 0) = 0$ với $i \in \mathbb{N}$
- $f(1, 1) = n$
- $f(i, j) = \left\lfloor \frac{f(i - 1, j)}{2} \right\rfloor + \left\lfloor \frac{f(i, j - 1)}{2} \right\rfloor$ với điều kiện $i, j \in \mathbb{Z}^{+}$ và $ij > 1$
Tìm số cặp $(i, j)$ sao cho $f(i, j)$ là một số nguyên lẻ.
Bài 3. Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Một đường tiếp tuyến với $(BOC)$ cắt $AB$ ở $D$ và $CA$ ở $E$. Gọi $A'$ là điểm đối xứng của điểm $A$ qua $DE$. Chứng minh rằng $(A'DE)$ tiếp xúc với $(ABC)$.
Ngày 2.
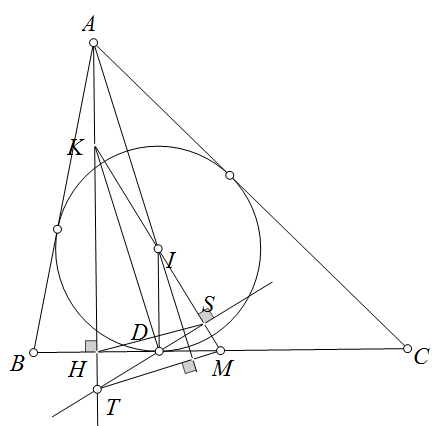
Bài 4. Cho $\triangle ABC$ và tâm nội tiếp $I$, $M$ là trung điểm của $BC$, $D$ là điểm tiếp xúc của $(I)$ với $BC$. Chứng minh rằng các đường vuông góc hạ từ $M, D, A$ lần lượt đến các đường $AI, IM, BC$ đồng quy.
Bài 5. Có $2n - 1$ tập con gồm hai phần tử của tập $S = \{1, 2, \cdots, n\}$. Chứng minh rằng ta có thể chọn ra $n$ tập con trong chúng sao cho hợp của $n$ tập này chứa không quá $\frac{2}{3}n + 1$ phần tử.
Bài 6. Cho $a_{1}, a_{2}, \cdots, a_{2^{2016}}$ là các số nguyên dương không lớn hơn $2016$. Biết rằng với mỗi $1 \le n \le 2^{2016}$ thì $a_{1}\cdots a_{n} + 1$ là một số chính phương. Chứng minh rằng có tồn tại một vài $i$ để $a_{i} = 1$.