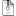Bài 54 (Azerbaijan JBMO TST). Với $a,b,c$ là ba số thực dương thỏa mãn điều kiện $a+b+c=3.$ Chứng minh rằng
\[2(ab+ac+bc)-3abc \geqslant a \sqrt{\frac{b^2+c^2}{2}}+b \sqrt{\frac{c^2+a^2}{2}}+c \sqrt{\frac{a^2+b^2}{2}}.\]
Em xin giải bài 54 bằng SOS
BĐT $<=> \frac{(ab+bc+ca)(a+b+c) -9abc}{3} \geq \sum a( \sqrt{\frac{b^2+c^2}{2}} - \frac{b+c}{2} )$
Nhân liệp hiệp và phân tích bình phương SOS, ta được
$\frac{\sum c(a-b)^2 }{3} \geq \sum \frac{c(a-b)^2}{\sqrt{8(a^2+b^2)} +2(a+b) } $
$<=> \sum (\frac{c}{3} - \frac{c}{\sqrt{8(a^2+b^2)} +2(a+b) }) (a-b)^2 \geq 0 $
Mà ta có $2(a^2+b^2 ) \geq (a+b)^2 $
Do đó $\sqrt{8(a^2+b^2)} +2(a+b) \geq 4(a+b) $
Ta chứng minh 1 bđt yếu hơn
$\sum c. \frac{4(a+b) -3}{12(a+b) } (a-b)^2 \geq 0 $
Đặt $S_c = \frac{4(a+b) -3}{12(a+b) } c $
Tương tự cho $S_a , S_b $
Đưa bđt về dạng $\sum S_a(b-c)^2 \geq 0 $ thì ta có
$S_c \geq 0 <=> 4(a+b) \geq 3 $ đúng do $a \geq 1 $
$S_b \geq 0 <=> 4(a+c) \geq 3 $ đúng do $a \geq 1 $
Bây giờ ta chứng minh $b^2S_a + a^2S_b \geq 0 <=> 4\frac{a+b}{3} \geq \frac{a}{a+c} +\frac{b}{b+c} $
Mà dễ thấy $\frac{a}{a+c} + \frac{b}{b+c} \leq 2 $
Do đó , ta cần chứng minh $4(a+b) \geq 6 $ mà này thì hiển nhiên do $3 = a+b+c \leq 2(a+b) => 4(a+b) \geq 6 $
Vậy, ta có điều phải chứng minh