Như vậy lời giải bài Tuần 5 tháng 3 đã được thầy Hùng đưa ra tại Tuần 1 tháng 4 và kèm theo đó là bài toán mới:
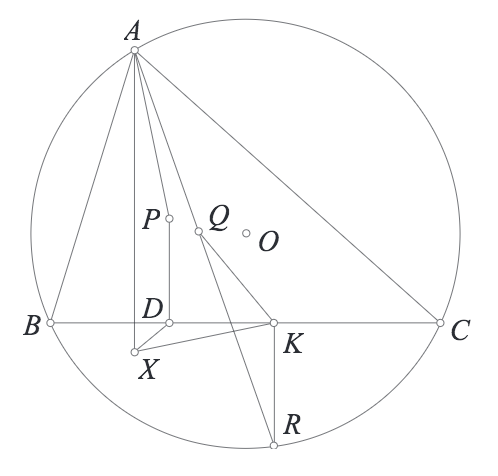
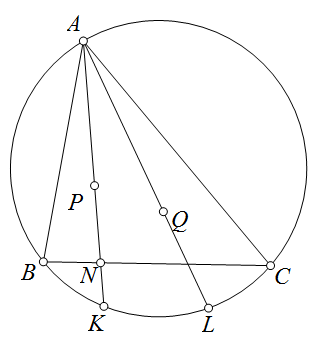
Bài 33. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ với $P,Q$ là hai điểm đẳng giác trong tam giác đó. $AQ$ cắt $(O)$ tại $R$ khác $A$. $D,K$ là hình chiếu của $P,R$ lên $BC$. Chứng minh rằng các đường thẳng qua $A,D,K$ lần lượt vuông góc với $BC,QK, AP$ đồng quy.
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 04-04-2016 - 03:54