KỲ THI HỌC SINH GIỎI CÁC TRƯỜNG THPT CHUYÊN
KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ
LẦN THỨ IX NĂM HỌC 2015-2016
ĐỀ THI MÔN TOÁN-KHỐI 10
Thời gian làm bài 180 phút (không kể thời gian giao đề)
Ngày thi 23/4/2016 (Đề thi gồm 01 trang)
$\boxed{\textrm{ĐỀ THI CHÍNH THỨC}}$
Bài 1 (4 điểm).
Giải hệ phương trình : $\left\{\begin{matrix} 7x^3+y^3+3xy(x-y)=12x^2-6x+1 & & \\ 2\sqrt{x^2+3}-\sqrt{9-y^2}+y=1 & & \end{matrix}\right.$
Bài 2 (4 điểm).
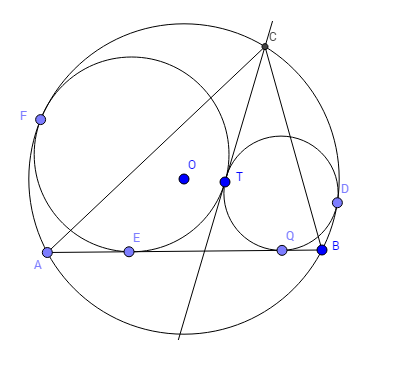
Cho đường tròn $(O)$ và dây $AB$ . Các đường tròn $(O_1)$ và $(O_2)$ nằm về một phía đối với đường thẳng $AB$ , tiếp xúc với nhau tại $T$ đồng thời tiếp xúc với $AB$ và tiếp xúc trong với đường tròn $(O)$. Tiếp tuyến chung tại $T$ của các đường tròn $(O_1)$ và $(O_2)$ cắt đường tròn $(O)$ tại $C$ (với $C$ thuộc nửa mặt phẳng với bờ là đường thẳng $AB$ có chứa hai đường tròn $(O_1)$ và $(O_2)$ ).Chứng minh rằng $T$ là tâm đường tròn nội tiếp của tam giác $ABC$
Bài 3 (4 điểm).
Cho $m$ và $n$ là các số nguyên dương thỏa mãn $2016^{m}+1$ là ước của $2016^{n}+1$ .Chứng minh rằng $m$ là ước của $n$.
Bài 4 (4 điểm)
Cho ba số dương $a,b,c$ thay đổi thỏa mãn $a+b+c=abc$.Chưng minh rằng:
$$3+\frac{b}{a^2}+\frac{c}{b^2}+\frac{a}{c^2}\geq \left ( \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \right )^2+\sqrt{3}$$
Bài 5 (4 điểm)
Cho tập hợp $X$ có $2016$ phần tử.Chọn ra $64$ tập con $X_1,X_2,...,X_64$ của tập $X$ {mỗi tập con đều chứa nhiều hơn $1008$ phần tử} . Chứng minh rằng:tồn tại tập con $A$ của $X$ có số phần tử không vượt quá $6$ mà $A\cap X,\neq \oslash,i=\overline{1,64}$
HẾT