Em viết rõ chỗ "kết hợp định lý Ceva dạng lượng giác suy ra "... thầy nghĩ chỗ đó có vấn đề.

Lời giải halloffame, 02-01-2018 - 16:29
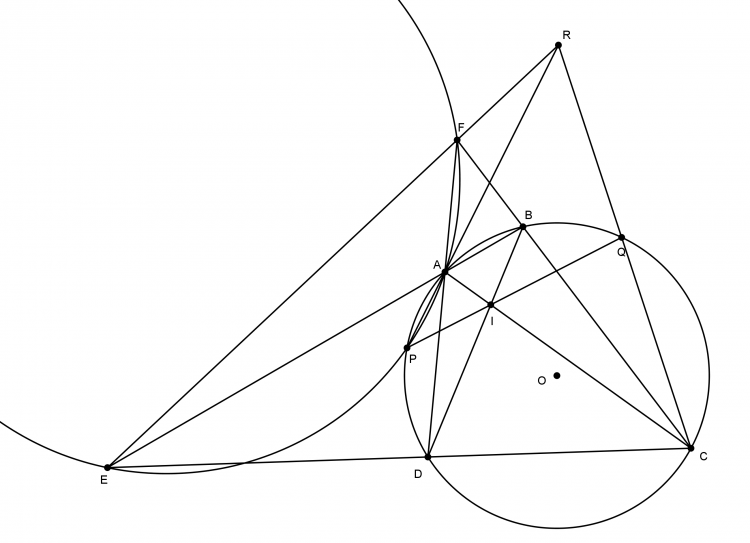
Lời giải bài toán 196. Ta chứng minh bài toán cho đường tròn $(K)$ tiếp xúc trong $(O),$ trường hợp tiếp xúc ngoài chứng minh tương tự. Ta thấy có thể bỏ đi điểm $B$ không cần thiết.
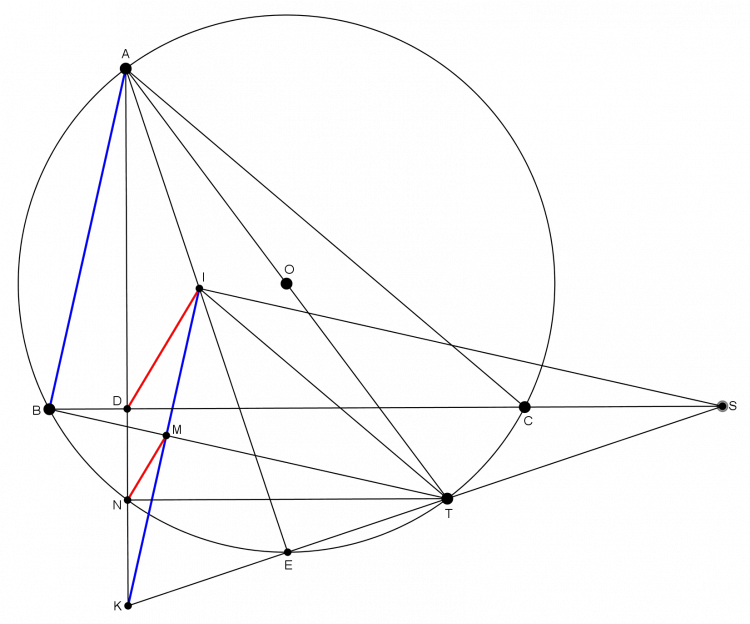
Bài toán 196'. $\Delta ADC$ vuông tại $D$ nội tiếp $(O),$ một đường tròn $(E)$ tiếp xúc trong $(O)$ ở $T.M,N \in (E)$ sao cho $MN \parallel AD$ và $MN=AD.P,R$ là trung điểm $MD,MC.$ Khi đó $P \in (ORT).$
Chứng minh.
$M'$ đối xứng $M$ qua $T.$ Dựng điểm $I$ sao cho $OEMI$ là hình bình hành.
$OI$ cắt $(O),CD$ ở $K,L.J$ là hình chiếu $I$ lên $CD.$
Từ $OEMI$ là hình bình hành và $EM=ET$ ta suy ra được $IK=IM=JN,LK=LM$
Gọi $Q$ đối xứng $M$ qua $O$ thì $Q \in LM'.$ Ta có $LM'.LQ=LK.NJ=LK.KI=KO^2-OL^2=LC.LD \Rightarrow Q \in (M'CD).$
Qua phép vị tự tâm $M$ tỉ số $\frac{1}{2}$ ta có ngay đpcm.
[attachment=33194:Screen Shot 2018-01-02 at 1.29.42 AM.png]
Đi đến bài viết »
#361
 Đã gửi 08-02-2017 - 22:51
Đã gửi 08-02-2017 - 22:51

#362
 Đã gửi 09-02-2017 - 00:21
Đã gửi 09-02-2017 - 00:21

E xin trình bày lời giải khác cho bài toán $164$ theo cách thuần túy hình học:
Bài toán trên là sự kết hợp của $2$ bổ đề:
Bổ đề 1: Cho $\triangle ABC$ nội tiếp $(O)$, tâm nội tiếp $I$. $AI$ cắt $(O)$ tại điểm thứ $2$ là $K$. Đường thẳng qua $K$ vuông góc với $AK$ cắt đường cao xuất phát từ $A$ của $\triangle ABC$ và $BC$ lần lượt tại $N,M$. CMR: $\angle MIN=90^{\circ}$
C/m: Kẻ đường kính $AD$ của $(O)$ thì $D$ đối xứng $N$ qua $K$. Gọi $AN$ cắt $BC$ tại $E$
Dễ thấy các tứ giác $NEIM$ và $AEKM$ nội tiếp. Ta có: $\angle NIE=\angle NME=\angle KAN\Rightarrow\triangle NIE\sim\triangle NAI\Rightarrow NI^2=NE.NA=NK.NM\Rightarrow\triangle IMN$ vuông tại $I\Rightarrow\angle MIN=90^{\circ}$
Bổ đề 2: Cho $\triangle ABC$ nội tiếp $(O)$, tâm nội tiếp $I$. $AI$ cắt $(O)$ tại điểm thứ $2$ là $K$. Đường thẳng qua $K$ vuông góc với $AK$ cắt $BC$ tại $L$. $E,F$ lần lượt là tiếp điểm của đường tròn bàng tiếp trog góc $B,C$ trên $AC,AB$. CMR: $EF\parallel IL$
C/m: Kẻ $ID\perp BC$ ($D\in BC$). Gọi $KD$ cắt $(O)$ tại điểm thứ $2$ là $T$, $AK$ cắt $EF$ tại $P$
Ta có: $\frac{TB}{TC}=\frac{DB}{DC}=\frac{AF}{AE}\Rightarrow\triangle TBC\sim\triangle AFE\Rightarrow\triangle TBD\sim\triangle AFP\Rightarrow\angle EPK=\angle APF=\angle TDB=\angle LDK=\angle LIK\Rightarrow EF\parallel IL$
- canhhoang30011999 và quanghung86 thích
#363
 Đã gửi 09-02-2017 - 00:37
Đã gửi 09-02-2017 - 00:37

Lời giải bài toán 165. Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}$. Gọi phân giác $\angle BAC$ cắt $PQ$ tại $I$ do thì $\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$ nên $BI$ là phân giác $\angle ABC$. Từ đó $I$ là tâm nội tiếp và $CI$ là phân giác $\angle ACB$ đồng thời cũng là phân giác $\angle PCQ$ nên $\frac{CP}{CQ}=\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$, ta hoàn thành chứng minh.
Em đã viết ra và gửi thầy qua mail. Nhận xét của em đúng và lời giải thầy cần bổ sung thêm một đoạn cuối, cám ơn em. Thầy viết cẩn thận như sau
Lời giải bài toán 165. Khi $P=Q$ thì ta có kết luận hiển nhiên đúng.
Khi $P\not=Q$. Giả sử $\frac{AP}{AQ}=\frac{BP}{BQ}$. Gọi phân giác $\angle BAC$ cắt $PQ$ tại $I$ do thì $\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$ nên $BI$ là phân giác $\angle ABC$. Từ đó $I$ là tâm nội tiếp và $CI$ là phân giác $\angle ACB$ đồng thời cũng là phân giác $\angle PCQ$ nên $\frac{CP}{CQ}=\frac{IP}{IQ}=\frac{AP}{AQ}=\frac{BP}{BQ}$. Từ đó $(ABC)$ là đường tròn Apollonius của đoạn $PQ$ như vậy $I$ cũng nằm trên $(ABC)$ điều này vô lý.
- moonkey01 yêu thích
#364
 Đã gửi 09-02-2017 - 19:40
Đã gửi 09-02-2017 - 19:40

Được sự đồng ý của thầy Hùng, em đề nghị bài toán tiếp theo, cũng là 1 bài của thầy.
Bài toán 166. Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ bán kính $R$ có $I$ là tâm nội tiếp, $AD$ là đường cao. $K$ là điểm trên tia $AD$ sao cho $AK=2R$. $M$ là hình chiếu của $B$ trên $IK$. Gọi $AD$ cắt lại $(O)$ tại $N$. Giả sử rằng $IK\parallel AB$. Chứng minh rằng $MN\parallel ID$.
- canhhoang30011999, CaptainCuong và the unknown thích
#365
 Đã gửi 09-02-2017 - 21:23
Đã gửi 09-02-2017 - 21:23

Lời giải bài toán 166: Ko ngờ lại chung $1$ giuộc với bài của mình ![]()
Kẻ đường kính $AT$ của $(O)$. $AI$ cắt $(O)$ tại điểm thứ $2$ là $E$ thì $T$ đối xứng $K$ qua $E$. Gọi $KT$ cắt $BC$ tại $S$
Từ gt $\Rightarrow AB\perp BM\Rightarrow\overline{B,M,T}$. Do đó tứ giác $MNKT$ nội tiếp
Theo bổ đề $1$ bài toán $164$ thì tứ giác $IDKS$ nội tiếp. Ta có biến đổi góc:
$\angle KMN=\angle KTN=\angle KSD=\angle KID\Rightarrow MN\parallel ID$
Bài viết đã được chỉnh sửa nội dung bởi Dark Repulsor: 09-02-2017 - 21:24
- canhhoang30011999 và moonkey01 thích
#366
 Đã gửi 09-02-2017 - 22:25
Đã gửi 09-02-2017 - 22:25

Bài toán 167: Cho $\triangle ABC$, tâm nội tiếp $I$, tâm bàng tiếp $J$ trog góc $A$. Gọi $D$ là trung điểm của $IJ$. Đường thẳng qua $I$ song song với $BC$ cắt $DB,DC$ lần lượt tại $P,Q$. $JB$ cắt $IC$ tại $M$, $JC$ cắt $IB$ tại $N$. Các đường thẳng đối xứng với $PQ$ qua $BM,CN$ cắt nhau tại $K$. Tìm điều kiện của $\triangle ABC$ để $I$ là trung điểm của $KJ$
- canhhoang30011999 và moonkey01 thích
#367
 Đã gửi 10-02-2017 - 19:48
Đã gửi 10-02-2017 - 19:48

Lời giải bài toán 167:
Dễ thấy rằng $M, N$ thứ tự là tâm bàng tiếp góc $C, B$ của $\triangle ABC$.
$PQ$ thứ tự cắt $BM, BA, CA, CN$ tại $X, Y, Z, T$. Do $PQ \parallel BC$ nên dễ thấy $\triangle YIB$ cân và ta suy ra $Y$ là trung điểm $IX$. $NB$ cắt $(MNP)$ tại $L$. Thế thì $XL \parallel YB$. Suy ra $XL$ đi qua đối xứng của $I$ qua $MN$. Do $XL$ đối xứng $PQ$ qua $JM$ nên tương tự ta sẽ suy ra được $K$ đối xứng $I$ qua $MN$ và $K \in (MNP)$.
Gọi $S, O$ thứ tự là tâm $(ABC)$ và $(MNP)$. Ta có $I$ là trung điểm $KJ$ $\Leftrightarrow$ $OI \perp KJ$ $\Leftrightarrow$ $IS \perp AD$ $\Leftrightarrow$ $I$ là trung điểm $AD$. Áp dụng định lí Ptolemy ta suy ra $AB+AC=2BC$.
- canhhoang30011999, moonkey01 và LinhToan thích
#368
 Đã gửi 11-02-2017 - 18:19
Đã gửi 11-02-2017 - 18:19

Theo đề nghị của anh Khánh, em đề xuất bài toán tiếp theo, có lẽ là của anh Phạm Hy Hiếu, HCB IMO năm 2009.
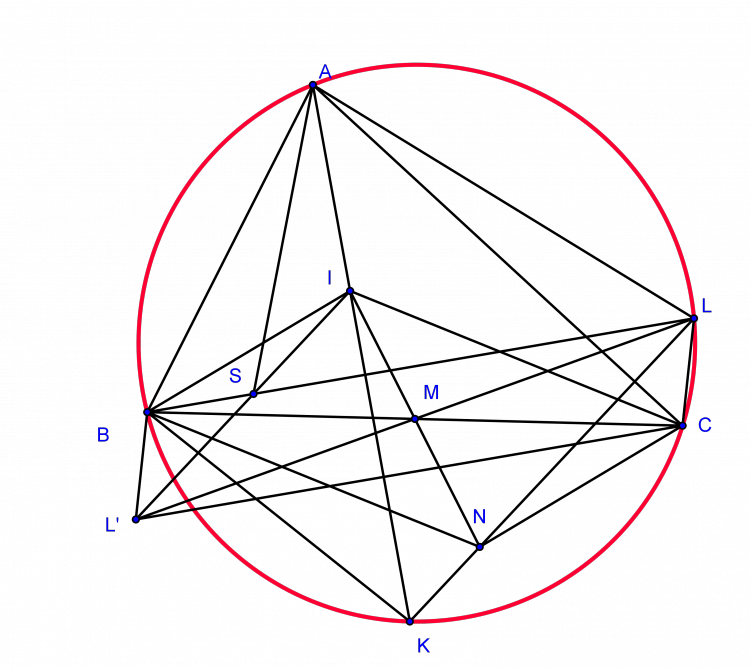
Bài toán 168. Cho tam giác $ABC$ nội tiếp $(O)$ có $BC>CA>AB$ và $I$ là tâm nội tiếp. $AI$ cắt lại $(O)$ tại $K$. $M$ là trung điểm $BC$. Gọi $N$ đối xứng với $I$ qua $M$. $KN$ cắt lại $(O)$ tại $L$. Chứng minh rằng $LB=LC+LA$.
#369
 Đã gửi 12-02-2017 - 13:04
Đã gửi 12-02-2017 - 13:04

Theo đề nghị của anh Khánh, em đề xuất bài toán tiếp theo, có lẽ là của anh Phạm Hy Hiếu, HCB IMO năm 2009.
Bài toán 168. Cho tam giác $ABC$ nội tiếp $(O)$ có $BC>CA>AB$ và $I$ là tâm nội tiếp. $AI$ cắt lại $(O)$ tại $K$. $M$ là trung điểm $BC$. Gọi $N$ đối xứng với $I$ qua $M$. $KN$ cắt lại $(O)$ tại $L$. Chứng minh rằng $LB=LC+LA$.
Mãi mới có thời gian rảnh để làm. Bài này vẽ hình phụ khá đơn giản nhưng rất đẹp.
Trên $LB$ lấy $S$ sao cho $LS=LA$.
Ta có: $\widehat{ASB}=180^o-\widehat{ASL}=180^o-\dfrac{180^o-\widehat{ALS}}{2}=90^o+\dfrac{\widehat{ALS}}{2}=90^o+\dfrac{\widehat{ACB}}{2}=\widehat{AIB}$
Từ đó tứ giác $AISB$ là tứ giác nội tiếp. Lấy $L'$ đối xứng với $L$ qua $M$. Theo tính đối xứng thì $LC=L'B$
Ta có: $\widehat{ISL}=\widehat{BAI}=\widehat{BLK}$ nên $IS \parallel KL$. Mà do tính đối xứng thì $IL' \parallel KL$ nên $I,L',S$ thẳng hàng
Do cần chứng minh :$LB=LC+LA$ mà $LS=LA$ và $LC=L'B$ nên chỉ cần chứng minh $BS=BL'$
Hay cần chứng minh tam giác $BSL'$ cân tại $B$. Tương đương: $\widehat{L'BS}=180^o-2\widehat{BSL'}=180^o-2\widehat{BAI}=180^o-\widehat{BAC}$
Mà do $BL' \parallel LC$ nên $\widehat{L'BS}=180^o-\widehat{BLC}=180^o-\widehat{BAC}$
Từ đó tam giác $BSL'$ cân tại $B$
Kết hợp những điều trên ta có điều phải chứng minh $\blacksquare$
- CaptainCuong, minhrongcon2000, moonkey01 và 1 người khác yêu thích
#370
 Đã gửi 12-02-2017 - 14:42
Đã gửi 12-02-2017 - 14:42

Theo đề nghị của anh Phương, em đề xuất tiếp bài toán sau của thầy Hùng.
Bài toán 169. Cho tam giác $ABC$ có $D$ là điểm bất kỳ trên đường cao từ $A$. Đường tròn $(K)$ đường kính $AD$ cắt $CA,AB$ tại $E,F$. Tiếp tuyến tại $E,F$ của $(K)$ cắt $BC$ tại $M,N$. Gọi $EB$ cắt $FC$ tại $P$, $EN$ cắt $FM$ tại $Q$. Chứng minh rằng $PQ$ luôn đi qua điểm cố định khi $D$ thay đổi.
- hohohoho yêu thích
#371
 Đã gửi 12-02-2017 - 21:30
Đã gửi 12-02-2017 - 21:30

Lời giải bài toán 169: Bài này chỉ cần $B,C$ cố định là đc
Ta sẽ tổng quát bt trên: Cho $\triangle ABC$. Lấy $E\in AB$, $F\in AC$, $M,N\in BC$. Gọi $EM$ cắt $FN$ tại $P$, $EN$ cắt $FM$ tại $Q$, $BF$ cắt $CE$ tại $S$. CMR: $SP,AQ,BC$ đồng quy
C/m: Gọi $AQ$ cắt $BC$ tại $K$. Áp dụng $Menelaus$ cho các tam giác $AEC$, $FMC$, $EMQ$ và tứ giác $AEQF$ ta có:
$(\frac{FA}{FC}.\frac{SC}{SE}.\frac{BE}{BA}).(\frac{AC}{AF}.\frac{QF}{QM}.\frac{KM}{KC}).(\frac{PE}{PM}.\frac{FM}{FQ}.\frac{NQ}{NE})=1$
$\Rightarrow\frac{SE}{SC}.\frac{KC}{KM}.\frac{PM}{PE}=\frac{BE}{BA}.\frac{CA}{CF}.\frac{MF}{MQ}.\frac{NQ}{NE}=1$
$\Rightarrow\overline{S,K,P}$ ($Menelaus$ đảo cho $\triangle EMC$) $\Rightarrow$ đpcm
Trở lại bt: Gọi $EM$ cắt $FN$ tại $S$ thì $S$ là giao $2$ tt tại $E$ và $F$ của $(AD)$ nên $AS$ là đường đối trung của $\triangle AEF$. Mà $EF$ đối song $BC$ nên $AS$ chia đôi $BC$. Vậy $PQ$ đi qua trung điểm của $BC$ cố định
- moonkey01 yêu thích
#372
 Đã gửi 13-02-2017 - 22:03
Đã gửi 13-02-2017 - 22:03

Bài toán 170: Cho $\triangle ABC$. $M\in (BC)$ sao cho $M$ nằm trog $\triangle ABC$. Gọi $D,E,F$ lần lượt là hình chiếu của $M$ trên $BC,CA,AB$. $ME$ cắt $AB$ tại $P$, $MF$ cắt $AC$ tại $Q$, $PQ$ cắt $BC$ tại $K$. $H$ đối xứng với $M$ qua trung điểm của $PQ$. CMR: $HK\perp AD$
- minhrongcon2000 và moonkey01 thích
#373
 Đã gửi 15-02-2017 - 12:28
Đã gửi 15-02-2017 - 12:28

Bài toán 170: Cho $\triangle ABC$. $M\in (BC)$ sao cho $M$ nằm trog $\triangle ABC$. Gọi $D,E,F$ lần lượt là hình chiếu của $M$ trên $BC,CA,AB$. $ME$ cắt $AB$ tại $P$, $MF$ cắt $AC$ tại $Q$, $PQ$ cắt $BC$ tại $K$. $H$ đối xứng với $M$ qua trung điểm của $PQ$. CMR: $HK\perp AD$
Lời giải sau tham khảo từ Nguyễn Lê Phước trên Facebook.
Lời giải: Ta có hai tam giác $PBM$ và $QMC$ đồng dạng g.g do $\angle PBM=90^{\circ}-\angle BMF=\angle QMC$ và $\angle BPM=\angle MQC$, từ đó $\frac{PB}{QM}=\frac{PM}{QC}$. Dễ thấy rằng $MPHQ$ là hình bình hành nên $MQ=HP$ và $MP=HQ$, từ đó $\frac{PB}{PH}=\frac{QH}{QC}$ hay tam giác $PBH$ đồng dạng tam giác $QHC$ (c.g.c). Gọi $R$ là hình chiếu của $H$ trên $BC$ thì $\angle PRQ=\angle PRH+\angle QRH=\angle PBH+\angle QCH=90^{\circ}$, lại theo một bài toán quen thuộc là $ND=NR$ nên các điểm $D,E,F,P,Q,R$ thuộc một đường tròn. Gọi $HK$ cắt $(APQ)$ tại $S$ thì $KD.KR=KP.KQ=KH.KS$ dẫn đến $DSHR$ nội tiếp. Do đó $\angle DSH=90^{\circ}=\angle ASH$ nên $A,S,D$ thẳng hàng. Vậy $AD\perp HK$ $\blacksquare$
Một kết quả thú vị cho bài toán: $M.H$ là hai điểm đẳng giác trong tam giác $ABC$.
Bài viết đã được chỉnh sửa nội dung bởi moonkey01: 15-02-2017 - 12:31
- manhhung2013, quanghung86 và the unknown thích
#374
 Đã gửi 15-02-2017 - 15:27
Đã gửi 15-02-2017 - 15:27

Bài toán 171 (Kiểm tra dự tuyển 10 THPT chuyên KHTN). Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ và trực tâm $H$. Đường tròn đường kính $AH$ cắt $(O)$ tại $G$ khác $A$. Đường thẳng qua $A$ vuông góc với $GA$ cắt $OB,OC$ lần lượt tại $M,N$. $AH$ cắt $OB,OC$ theo thứ tự tại $P,Q$. $MQ$ cắt $NP$ tại $R$. Chứng minh rằng $AR$ song song đường thẳng Euler của tam giác $ABC$.
- ecchi123, moonkey01 và yeutoan2001 thích
#375
 Đã gửi 15-02-2017 - 19:40
Đã gửi 15-02-2017 - 19:40

Bài 171 : ta có $A(ROHM)=-1$ , Gọi $I$ là trung điểm $H$ thì $OI$ vuông góc $AG$ ,$OH$ cắt $AM$ tại $K$ thì $O$ là trung điểm $HK$ , mà $A(ROHM)=-1$ nên $AR$ song song $OH$
Bài viết đã được chỉnh sửa nội dung bởi ecchi123: 15-02-2017 - 19:43
- moonkey01 và Subtract Zero thích
![]()
![]()
![]()
#376
 Đã gửi 15-02-2017 - 20:27
Đã gửi 15-02-2017 - 20:27

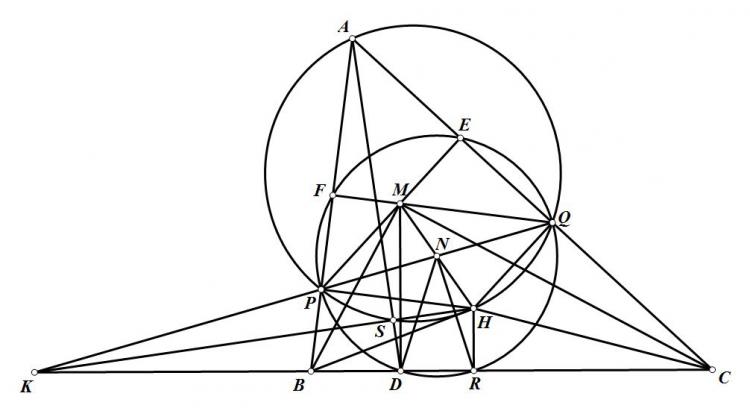
Bài 172 (sáng tác từ một bài toán của bạn Bảo ) : Cho tam giác $ABC$ cố định có đường cao $AH$ , $P$ di chuyển trên tia đối của tia $HC$ , $M$ đối xứng với $C$ qua $H$ . $MN$ song song với $AC$ với $N$ thuộc $AP$ . $Q$ là trung điểm $AH$ . $PQ$ cắt $HN$ tại $D$. Đường tròn $(X)$ thay đổi qua $D$ và tiếp xúc với đường tròn euler của tam giác $AHD$ cắt $DA,DH$ tại $F,E$ . Chứng minh : $(XFE)$ tiếp xúc với đường thẳng cố định khi $P$ và $(X)$ thay đổi
Bài viết đã được chỉnh sửa nội dung bởi ecchi123: 18-02-2017 - 18:32
- moonkey01 yêu thích
![]()
![]()
![]()
#377
 Đã gửi 23-02-2017 - 00:17
Đã gửi 23-02-2017 - 00:17

Lời giải bài 172 :
Trước tiên ta chứng min bổ đề sau :
Bổ đề : Cho $\triangle ABC$. Đường tròn $(X)$ bất kì qua $A$ tiếp xúc với đường tròn Euler cắt $AB,AC$ tại $M,N$. Chứng minh rằng đường tròn $(XMN)$ tiếp xúc với đường trung bình của $\triangle ABC$
Chứng minh : Xét phép nghịch đảo $I^A_k$, bài toán trên trở thành : Cho $\triangle ABC$ nội tiếp $(O)$. Đường thẳng bất kì tiếp xúc $(BOC)$ cắt $CA,AB$ tại $M,N$. $D$ đối xứng $A$ qua $MN$. Khi đí $(DMN)$ tiếp xúc $(O)$ ( đây chính là bài toán SMO 2016 ở đây https://www.artofpro...1220645p6102531 )
Áp dụng : Gọi $T$ là trung điểm $MH$
Theo định lý Menelaus ta có : $1 = \frac{\overline{DQ}}{\overline{DP}}.\frac{\overline{NP}}{\overline{NA}}.\frac{\overline{HA}}{\overline{HQ}}= \frac{\overline{DQ}}{\overline{DP}}.\frac{\overline{MP}}{\overline{MC}}.2=\frac{\overline{DQ}}{\overline{DP}}\frac{\overline{MP}}{\overline{MH}} \implies \frac{\overline{DQ}}{\overline{DP}}=\frac{\overline{MH}}{\overline{MP}}$ nên $MD \perp BC$
Ta có đường trung bình của $\triangle DAH$ tiếp xúc $(XMN)$ theo bổ đề, mà đường trung bình này chính là đường thẳng qua $T$ vuông góc $BC$ nên $(XMN)$ tiếp xúc đường thẳng cố định là đường qua trung điểm $MH$ vuông góc $BC$
Bài viết đã được chỉnh sửa nội dung bởi manhtuan00: 23-02-2017 - 00:19
#378
 Đã gửi 25-02-2017 - 10:55
Đã gửi 25-02-2017 - 10:55

Bài toán 173. Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$, $E$ là giao điểm của $AB$ với $CD$, $F$ là giao điểm của $AD$ với $BC$ . $(AEF)$ cắt $(O)$ tại $P$, $(CEF)$ cắt $O$ tại $Q$. $AC$ cắt $BD$ tại $I$. Chứng minh rằng $P,I,Q$ thẳng hàng.
Bài viết đã được chỉnh sửa nội dung bởi halloffame: 28-02-2017 - 23:15
- ecchi123, CaptainCuong, minhrongcon2000 và 1 người khác yêu thích
#379
 Đã gửi 25-02-2017 - 15:47
Đã gửi 25-02-2017 - 15:47

Lời giải bài 173:
Mình xin đề xuất một cách giải không mấy sơ cấp cho bài này:
Bài toán có thể được viết lại như sau: Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ có $AB$ cắt $CD$ tại $E$, $AD$ cắt $BC$ tại $F$ và $AC$ cắt $BD$ tại $I$. Gọi $P$ là giao điểm thứ hai của đường tròn $(AEF)$ và $(O)$. $PI$ cắt $(O)$ tại điểm thứ hai là $Q$. Chứng minh rằng $C$, $Q$, $F$, $E$ cùng thuộc 1 đường tròn.
Chứng minh:
Gọi $R$ là giao điểm của $AP$ và $CQ$.
Ta có $EF$ chính là đường đối cực của $I$ qua $(O)$.
Mặt khác, do $AP$ cắt $CQ$ tại $R$ và $AC$ cắt $PQ$ tại $I$ nên ta có $R$ nằm trên đường đối cực của $I$ qua $(O)$, hay nói cách khác $AP$, $EF$, $CQ$ cùng đồng qui tại 1 điểm.
Do đó, ta có được $\overline{RF}.\overline{RE}=\overline{RA}.\overline{RP}=\overline{RQ}.\overline{RC}\Rightarrow$ tứ giác $CQFE$ nội tiếp nên ta có điều phải chứng minh.$\square$
Bài viết đã được chỉnh sửa nội dung bởi minhrongcon2000: 25-02-2017 - 15:51
- ecchi123 và CaptainCuong thích
$\lim_{x \to \infty } Love =+\infty$
#380
 Đã gửi 25-02-2017 - 19:14
Đã gửi 25-02-2017 - 19:14

Bài toán 174. Cho $\Delta ABC$ có 1 điểm $D$ bất kì thuộc đường thẳng $BC$ sao cho $D$ và $B$ nằm khác phía so với $C$. Gọi $I$ và $I_1$ l ần lượt là tâm nội tiếp $\Delta ABC$ và $\Delta ACD$. Chứng minh rằng trục đẳng phương của $(I)$ và $(I')$ đi qua 1 điểm cố định khi $D$ thay đổi.
Bài viết đã được chỉnh sửa nội dung bởi halloffame: 28-02-2017 - 23:15
- ecchi123 yêu thích
$\lim_{x \to \infty } Love =+\infty$
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: hình học

|
Chứng minh PQ.CB=DC.QN và O là trung điểm của PQ.Bắt đầu bởi nonamebroy, Hôm qua, 10:24 |
|

|
|

|
Chứng minh tứ giác MAOB nội tiếp đường tròn.Bắt đầu bởi Phuockq, 07-04-2024 |
|

|
|

|
Toán thi Học sinh giỏi và Olympic →
Hình học →
Chứng minh B,M,N,C đồng viênBắt đầu bởi VGNam, 22-02-2024 |
|

|
|

|
Chứng minh ba điểm E, F, H thẳng hàng.Bắt đầu bởi Saturina, 16-02-2024 |
|

|
|

|
Toán thi Học sinh giỏi và Olympic →
Hình học →
a) Chứng minh rằng K thuộc đường tròn đường kính BC . b) Chứng minh rằng IMC KGJ 45oBắt đầu bởi Saturina, 16-02-2024 |
|

|
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh