Chủ đề này có 434 trả lời

[viet nam in my heart]

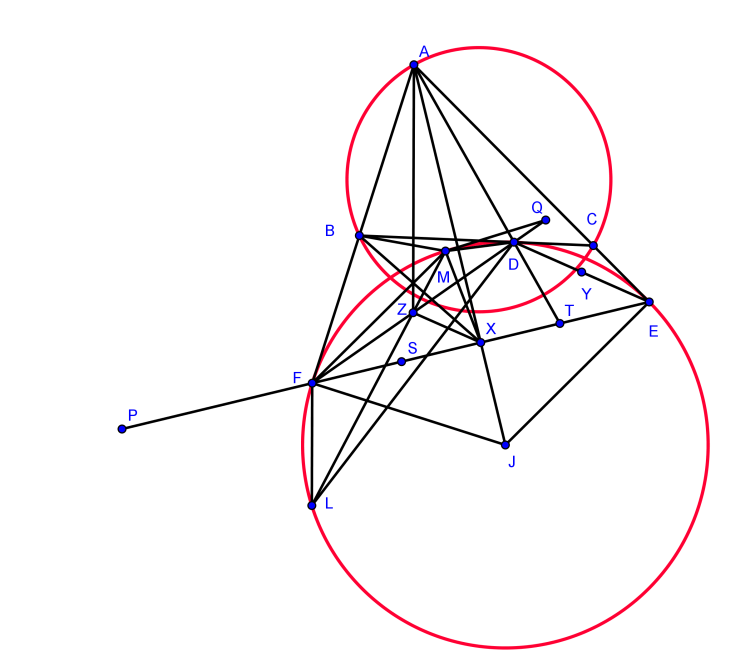
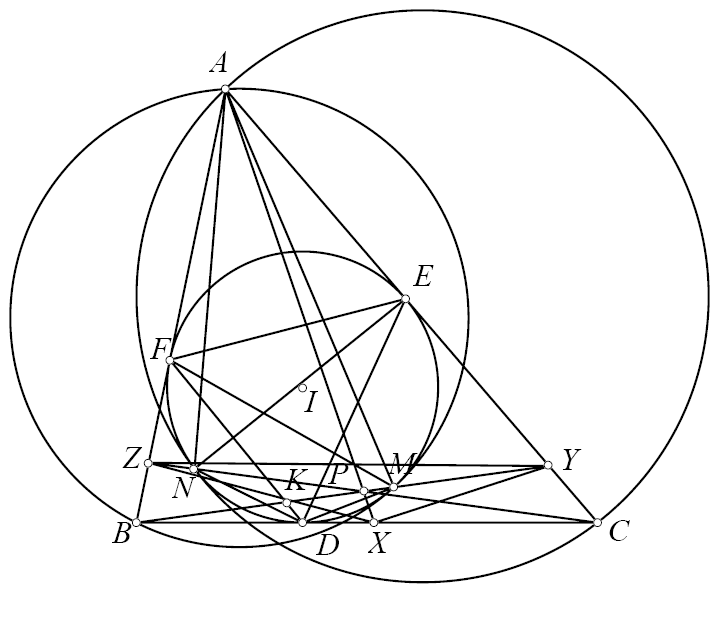
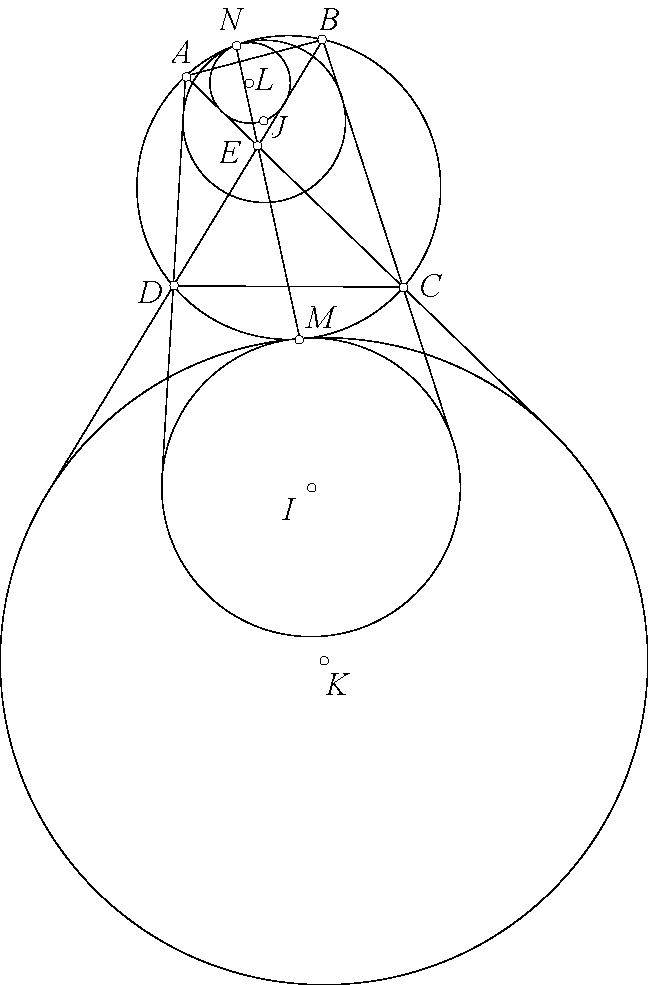
Bài toán 136. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ đường tròn bàng tiếp góc $A$ là $(J)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(J)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(J)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

 

Lời giải bài toán 136

Gọi $D,E,F$ là tiếp điểm của $(J)$ trên $BC,CA,AB$

Gọi $X,Y,Z$ là trung điểm $EF,DE,DF$

Ta chứng minh $BMXF$ và $CNXE$ nội tiếp 

Thật vậy nghịch đảo cực $A$ phương tích bất kỳ thì được cấu hình: tam giác $ABC$ với $(X)$ là đường tròn $A-Mixtilinear$ tiếp xúc với $AB,AC$ lại $F,E$. Tiếp tuyến thứ hai $BM$ đến $(K)$. Khi đó dễ thấy $B,M,X,F$ nội tiếp đường tròn

Từ đó nghịch đảo lại thì ở bài toán này $BMXF$ và $CNXE$ nội tiếp 

Xét phép nghịch đảo cực $D$ phương tích $JD^2$ thì ta thu được $AMZF$ và $ANYE$ nội tiếp

$AD$ cắt $EF$ tại $T$. $S$ đối xứng với $T$ qua $X$ thì do tam giác $AEF$ cân tại $A$ nên $AS,AT$ đẳng giác 

Do đó ta chứng minh $AS,BM,CN$ đồng quy. Xét cực và đối cực với $(J)$. Gọi $P,Q,R$ là cực của $AS,BM,CN$ với $(J)$.

Cần chứng minh $P,Q,R$ thẳng hàng

Khi đó theo định lý $Lahire$ thì $P,Q,R$ lần lượt nằm trên $EF,DF,DE$ nên ta sẽ áp dụng định lý $Menelaus$ để chứng minh

Thật vậy $(PSFE)=-1$ nên $\dfrac{PE}{PF}=\dfrac{SE}{SF}=\dfrac{TF}{TE}=\dfrac{DF^2}{DE^2}$ ( do $AD$ là đối trung của tam giác $DEF$)

Lại có: $Q$ là đối cực của $BM$ nên $QM$ tiếp xúc $(J)$. Từ đó :$\dfrac{QF}{QD}=\dfrac{MF^2}{MD^2}$

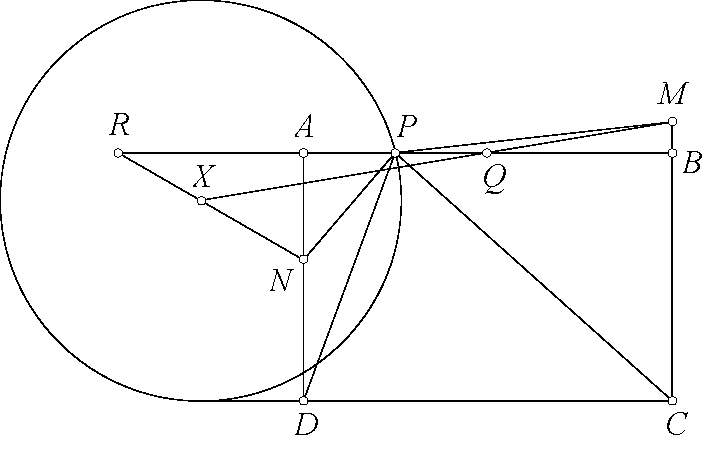
Giả sử $MZ$ cắt lại $(J)$ tại $L$. Ta có: $\widehat{AFZ}=\widehat{FLD}$ (góc tiếp tuyến) và $\widehat{FDL}=\widehat{FML}=\widehat{FAZ}$

Suy ra tam giác $FLD$ và tam giác $ZFA$ đồng dạng. Kết hợp $Z$ là trung điểm $DF$ nên ta thu được: $\dfrac{QF}{QD}=\dfrac{MF^2}{MD^2}=\dfrac{LD^2}{LF^2}=\dfrac{FA^2}{FZ^2}$

Tương tự: $\dfrac{RD}{RE}=\dfrac{EY^2}{EA^2}$. Từ đó $\dfrac{PE}{PF}.\dfrac{QF}{QD}.\dfrac{RD}{RE}=1$

Vậy ta có điều phải chứng minh

Ngoài ra ta hoàn toàn có thể chứng minh được $BMXF$ và $AMZF$ nội tiếp mà hoàn toàn không cần đến phép nghịch đảo nhưng lời giải sẽ dài hơn

Bài toán 137. Cho tam giác $ABC$ có $AC>BC>AB$. Đường tròn bàng tiếp góc $A$ và đường tròn nội tiếp tam giác $ABC$ tiếp xúc với đường tròn $Euler$ của nó tại $T,T_a$. Gọi $D,E$ là hình chiếu của $B,C$ lên $AC,AB$. Gọi $M,N$ là trung điểm $AC,AB$. Chứng minh $MN,DE,TT_a$ đồng quy 

Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 20-01-2017 - 18:28

[quanghung86]

Cám ơn Phương. Bài này mình cũng đã post trên AoPS ở đây và đáp án này cũng do mình đề nghị. Trước hết ta viết bài toán lại cho đường tròn nội tiếp cho dễ nhìn, hai cách viết chứng minh giống hết nhau

 

Bài toán 136'. Cho tam giác $ABC$ với đường tròn nội tiế $(I)$ tiếp xúc $BC$ tại $D$. Đường tròn qua $A,B$ tiếp xúc $(I)$ tại $M$. Đường tròn qua $A,C$ tiếp xúc $(I)$ tại $N$. $BM$ cắt $CN$ tại $P$. Chứng minh rằng $\angle PAB=\angle DAC$.

 

Bổ đề. Cho tam giác $ABC$ với đường tròn nội tiếp $(I,r)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. Đường tròn qua $B,C$ tiếp xúc $(I)$ tại $X$ thì

 

i) $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

 

ii) $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}.$

 

 

Chứng minh. Sử dụng chứng minh trong bài G7 SL 2002 quen thuộc, gọi $DK$ là đường kính của $(I)$ thì $XK,EF,BC$ đồng quy tại $G$. $AD$ cắt $EF$ tại $H$. Ta có $\frac{XE}{XF}.\frac{KE}{KF}=\frac{GE}{GF}=\frac{HE}{HF}=\frac{[AED]}{[AFD]}=\frac{DE}{DF}.\frac{DB}{IC}.\frac{IB}{DC}$ và chú ý $KE.IC=2r^2=KF.IB$. Vậy nên $\frac{XE}{XF}=\frac{IB.DE^2}{IC.DF^2}$ và $\frac{FX}{FK}.\frac{EX}{EK}=\frac{GX}{GK}=\frac{GD^2}{GK^2}=\frac{XD^2}{4r^2}$ và chú ý $KE.IC=2r^2=KF.IB$. Nên $\frac{XE.XF}{XD^2}=\frac{r^2}{IB.IC}.$

 

Hệ quả. $\dfrac{XE^2}{XD^2}=\dfrac{r^2.DE^2}{IB^2.DF^2}$ and $\dfrac{XF^2}{XD^2}=\dfrac{r^2.DF^2}{IC^2.DE^2}$.

 

 

Giải bài toán. Gọi $(I)$ tiếp xúc $CA,AB$ tại $E,F$. $XYZ$ là tam giác Ceva của $P$. Gọi $BY$ cắt $DF$ tại $K$. Ta có $\frac{YC}{YA}=\frac{[YBC]}{[YBA]}=\frac{[YBC]}{[KBD]}.\frac{[KBD]}{[KBF]}.\frac{[KBF]}{[YBA]}=\frac{BC.BY}{BD.BK}.\frac{KD}{KF}.\frac{BF.BK}{BY.BA}=\frac{BC}{BA}\frac{MD^2}{MF^2}=\frac{BC}{BA}.\frac{r^2.DF^2}{EF^2.IA^2}.$ Tương tự, $\frac{ZB}{ZA}=\frac{BC}{CA}.\frac{r^2.DE^2}{EF^2.IA^2}$. Sử dụng định lý Ceva thì $\frac{XB}{XC}=\frac{YA}{YC}.\frac{ZB}{ZA}=\frac{AB.DE^2}{AC.DF^2}$. Vì vậy nên $\frac{DB}{DC}.\frac{XB}{XC}=\frac{p-b}{p-c}.\frac{AB.DE^2}{AC.DF^2}=\frac{DF.IB}{DE.IC}.\frac{AB.DE^2}{AC.DF^2}=\frac{AB^2}{AC^2}$. Do đó $AD,AX$ đẳng giác.

[quanghung86]

Bài này của Phương thực chất là một bổ đề khá quen thuộc sau

 

Bổ đề. Tứ giác $ABCD$ nội tiếp đường tròn $(O)$. Đường tròn $(I)$ tiếp xúc $AD,BC$ và tiếp xúc ngoài cung nhỏ $CD$ tại $M$. Đường tròn $(J)$ tiếp xúc $AD,BC$ và tiếp xúc trong cung nhỏ $AB$ tại $N$. Chứng minh rằng $MN,BD,AC$ đồng quy.

 

 

Chứng minh. Theo bổ đề Poncelet thì đường tròn $(K)$ tiếp xúc $DB,DC$ tiếp xúc ngoài cung nhỏ $CD$ thì tiếp điểm cũng là $M$. Tương tự đường tròn $(L)$ tiếp xúc $DB,DC$ tiếp xúc trong cung nhỏ $AB$ thì tiếp điểm cũng là $N$. Gọi $DB$ cắt $AC$ tại $E$ thì $E$ là tâm vị tự trong của $(K),(L)$ nên theo định lý Monge thì $M,N,E$ thẳng hàng hay $MN,BD,AC$ đồng quy.

 

 

Giải bài toán. Áp dụng bổ đề cho tứ giác $MEND$ nội tiếp. Ta thu được điều phải chứng minh.

 

Bài toán 138 (Mở rộng T12/471 THTT). Cho tam giác $ABC$ nội tiếp $(O)$ và tâm nội tiếp $I$. $D$ thuộc cung $BC$ không chứa $A$ của $(O)$. $DB,DC$ cắt $(IAB),(ICA)$ tại $P,Q$ khác $B,C$. $M,N$ thuộc $BC$ sao cho $MP,QN$ cùng vuông góc với $PQ$. Chứng minh rằng tâm đường tròn $(AMN)$ nằm trên $DO$.

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 20-01-2017 - 19:21
Sửa link

[baopbc]

Lời giải bài toán 138. Dễ thấy $M,I,N$ thẳng hàng, ta có $\angle PMA=180^\circ-\angle AIB=\frac{1}{2}\cdot (\angle A+\angle B)=90^\circ-\frac{1}{2}\cdot \angle C=90^\circ-\frac{1}{2}\cdot \angle MPA$ nên $\triangle MPA$ cân suy ra $\overline{PA}=\overline{PM}$. Tương tự thì $\overline{PA}=\overline{PN}$ nên $P$ là tâm đường tròn ngoại tiếp tam giác $AMN$.Gọi $E,F$ lần lượt là giao điểm của $AP$ với các đường tròn $(AIB)$ và $(AIC)$. Do $\measuredangle AEM=\measuredangle ABM=\measuredangle ACP$ nên $ME\perp OP$. Tương tự thì $NF\perp OP$ do đó $ME\parallel NF$. Gọi $S,T$ lần lượt là giao điểm của $PB,PC$ với đường thẳng qua $A$ vuông góc với $PO$. Do $ST\parallel ME\parallel NF$ nên theo định lí Thales \[\frac{\overline{SM}}{\overline{SP}}=\frac{\overline{AE}}{\overline{AP}},\frac{\overline{TP}}{\overline{TN}}=\frac{\overline{AP}}{\overline{AF}}\Rightarrow \frac{\overline{SM}}{\overline{SP}}\cdot \frac{\overline{TP}}{\overline{TN}}=\frac{\overline{AE}}{\overline{AF}}\] Mặt khác do các tam giác $APM$ và $APN$ cân tại $P$ nên $BE\parallel AM, CF\parallel AN$ suy ra $\overline{AE}=\overline{MB}, \overline{AF}=\overline{NC}$. Do đó $\overline{AE}:\overline{AF}=\overline{MB}:\overline{NC}$. Gọi $X$ là giao điểm của $MN$ với $ST$. Áp dụng định lí Menelaus cho tam giác $SPT$, cát tuyến $M,N,X$ ta suy ra \[\frac{\overline{SM}}{\overline{SP}}\cdot \frac{\overline{TP}}{\overline{TN}}\cdot \frac{\overline{XN}}{\overline{XM}}=1\Rightarrow \frac{\overline{AE}}{\overline{AF}}=\frac{\overline{XM}}{\overline{XN}}\Rightarrow \frac{\overline{MB}}{\overline{NC}}=\frac{\overline{XM}}{\overline{XN}}\] Gọi $K,L$ lần lượt là giao điểm của $MQ,NR$ với đường thẳng $ST$. Theo định lí Thales \[\frac{\overline{KM}}{\overline{LN}}=\frac{\overline{XM}}{\overline{XN}}\Rightarrow\frac{\overline{KM}}{\overline{LN}}=\frac{\overline{MB}}{\overline{NC}}\] Mặt khác do $\overline{PM}=\overline{PN}$ nên $\triangle MPN$ cân tại $P$ nên $\measuredangle MNP=\measuredangle NMP$ suy ra $\measuredangle KMB=\measuredangle LNC$. Từ đó $\triangle KMB\sim \triangle LNC$ (cạnh - góc - cạnh) suy ra $\measuredangle KBM=\measuredangle LCN$. Do đó $\angle AKB=\angle KSB+\angle KBS=90^\circ-\angle OPB+\angle LCN=\angle BCP+\angle LCN=180^\circ-\angle BCL$ suy ra tứ giác $KBCL$ nội tiếp.\\ Gọi $Z$ là giao điểm của $ST$ với $BC$, theo tính chất phương tích $\overline{ZK}\cdot \overline{ZL}=\overline{ZB}\cdot \overline{ZC}$. Mặt khác do $\angle MKA=180^\circ-\measuredangle (PO,MN)=180^\circ-(\angle BMI+\angle BPO)=180^\circ-(\frac{1}{2}\cdot\angle A+\angle BPO)=90^\circ+\angle BAP$ $-\frac{1}{2}\cdot \angle A=90^\circ+\frac{1}{2}\angle A-\angle PBC=180^\circ-(90^\circ-\frac{1}{2}\angle A)-\angle MBQ=\angle BQM$ nên tứ giác $KLRQ$ nội tiếp suy ra $\overline{ZK}\cdot \overline{ZL}=\overline{ZQ}\cdot \overline{ZR}$. Do đó $\overline{ZB}\cdot \overline{ZC}=\overline{ZQ}\cdot \overline{ZR}$ nên $Z$ thuộc trục đẳng phương của các đường tròn $(O)$ và $(AQR)$ suy ra $AZ$ là trục đẳng phương của $(O)$ và $(AQR)$, từ đó suy ra tâm đường tròn ngoại tiếp tam giác $AQR$ thuộc $OP$ do $OP\perp AZ$. $\square$

[quanghung86]

Cám ơn Bảo với lời giải rất nhanh, thầy đề nghị bài mới cho topic tiếp tục

 

Bài toán 139 (Nguyễn Lê Phước).  Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $DE,DF$ cắt $AB,AC$ tại $M,N$. $IE,IF$ cắt $AB,AC$ tại $P,Q$. Chứng minh rằng trung điểm của $MN,PQ,BC$ thẳng hàng.

[manhtuan00]

Lời giải bài 139 : ( cách của em tính khá trâu bò ạ )

Ta có $(NE,AC) = -1$ nên $\frac{\overline{NA}}{\overline{NC}} = \frac{p-a}{p-c}$

Vậy tức là $\frac{\overline{NA}}{\overline{NA}+b}= \frac{p-a}{p-c}$ nên $\overline{NC} = |\frac{b(p-c)}{a-c}|$

Lại có $AQ = \frac{p-a}{cos \angle A}$ nên $CQ = b - AQ = b - \frac{p-a}{cos \angle A}$

Áp dụng đinh lý hàm cos có : $cos \angle A = \frac{b^2+c^2-a^2}{2bc}$

Vậy ta có $\overline{CQ} = \frac{b^3+bc^2-ba^2-b^2c-bc^2+abc}{b^2+c^2-a^2} = \frac{b^3-ba^2-b^2c+abc}{b^2+c^2-a^2}$

Vậy $\frac{\overline{CQ}}{\overline{CN}} = \frac{p-a}{cos \angle A}= |\frac{(b^3-ba^2-b^2c+abc)(a-c)}{(b^2+c^2-a^2)(p-c).b}| = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Tương tự ta có $\frac{\overline{BP}}{\overline{BM}} = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Nên $\frac{\overline{CQ}}{\overline{CN}}=\frac{\overline{BP}}{\overline{BM}}$ Áp dụng bổ đề E.R.I.Q  ta có trung điểm $MN,PQ,BC$ thẳng hàng

Hình gửi kèm

• 

[quanghung86]

Cách của thầy cũng giống hệt cách của Tuấn là tính hết ra và kết quả cuối cùng đúng như thế kia. Tuy nhiên Phước có cách giải thuần túy hình khá đẹp các bạn hãy cứ thử sức tiếp. Tuấn đề nghị một bài tiếp đi em!

[manhtuan00]

Bài toán 140 : (sách) Cho tứ giác $ABCD$ nội tiếp. Giả sử rằng tồn tại điểm $X$ để $\angle XAD = \angle XBA = \angle XCB = \angle XDC$. Chứng minh rằng tứ giác $ABCD$ điều hòa

Bài viết đã được chỉnh sửa nội dung bởi manhtuan00: 21-01-2017 - 10:31

[quanghung86]

Cám ơn Tuấn, xin trích dẫn lại lời giải của Telv ở #4 trong đây.

 

 

Giải bài toán 140 (Telv Cohl). Lấy điểm $Y$ sao cho hai tam giác $YBA$ và $XCD$ đồng dạng cùng hướng. Khi đó $\angle YAX+\angle YBX=\angle YAB+\angle BAX+\angle YBA+\angle ABX=\angle BAX+\angle XDC+\angle BAX+\angle XCD=180^\circ$. Từ đó $AYBX$ nội tiếp. Lại có $\angle YAB=\angle XDC=\angle XBA$ nên $AY\parallel BX$ do đó $AYBX$ là hình thang cân. Suy ra $AB^2=BY.AX+AY.BX$, lại có $YBA$ và $XCD$ đồng dạng nên $AB.CD=XA.XC+XB.XD$. Chứng minh tương tự $AD.BC=XA.XC+XB.XD$ nên $AB.CD=AD.BC$. Kết thúc chứng minh.

 

Bài toán 141. Cho bốn đường thẳng $\ell_1,\ell_2,\ell_3,\ell_4$ bất kỳ trong mặt phẳng. Gọi $H_1$ là trực tâm tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $P_1$ là cực trực giao của $\ell_1$ với tam giác tạo bởi các đường thẳng $(\ell_2,\ell_3,\ell_4)$. $X_1$ thuộc $\ell_1$ sao cho $P_1X_1\perp P_1H_1$. Định nghĩa tương tự các điểm $X_2,X_3,X_4$. Chứng minh rằng $X_1,X_2,X_3,X_4$ đồng viên.

[QuangDuong12011998]

Đây là đường tròn Hervey và em thấy nó khó tiếp cận nên em sẽ sử dụng tọa độ Oxy.

Cũng vì lời giải sau sử dụng tọa độ(cùng với vài kiến thức không phổ thông) nên em sẽ không đề xuất bài mới ạ.

_________________________________________________

Ý tưởng về cách chọn tọa độ: Với bài toán này, ta KHÔNG NÊN lấy 4 đường thẳng bất kì vì như vậy sẽ không có một quy luật nào và biến đổi đại số sẽ mất đi phần đẹp đẽ. Để xây dựng cách chọn, ta dựa trên một số tính chất của tứ giác toàn phần như sau.

Tính chất 1(tham khảo tại Epsilon 11 - Điểm Steiner. Điểm Anti-Steiner). Tồn tại duy nhất một parabola tiếp xúc với 4 đường thẳng của một tứ giác toàn phần cho trước và đường thẳng Steiner cũng chính là đường chuẩn của parabola này.

 

Như vậy đã rõ, ta sẽ lấy một đường parabola và chọn lấy 4 tiếp tuyến bất kì của nó - như vậy là đã bao quát được mọi trường hợp ! Tuy nhiên vì mọi parabola đều đồng dạng nên ta chỉ cần chọn parabola có phương trình $y=x^2$. Tiếp tuyến của parabola này tại điểm $(m,m^2)$ có phương trình $y=2mx-m^2$

Ta chọn ra 4 tiếp tuyến:

\[y=2x_1x-x_1^2\qquad y=2x_2x-x_2^2\qquad y=2x_3x-x_3^2\qquad y=2x_4x-x_4^2\]

Tính chất 2(http://forumgeom.fau...00406index.html) Với tứ giác toàn phần $(\ell_1,\ell_2,\ell_3,\ell_4)$, cực trực giao của $\ell_1$ với tam giác tạo bởi $(\ell_2,\ell_3,\ell_4)$ thuộc đường thẳng Steiner của tứ giác toàn phần đó.

_________________________________________________

Bắt đầu tính toán

Thay vì dẫn ra trực tiếp những tính toán thủ công, ta chỉ đưa ra các kết quả, công thức được sử dụng và nếu ra nó được dùng như thế nào.

Nhắc lại định nghĩa cực trực giao của $\ell$ với tam giác $ABC$: $D$, $E$, $F$ là hình chiếu vuông góc của $A$, $B$, $C$ lên $\ell$ thì đường thẳng qua $D$, $E$, $F$ và lần lượt vuông góc với $BC$, $CA$, $AB$ đồng quy tại cực trực giao của $\ell$ với tam giác $ABC$.

Như vậy ta sẽ cần tới công thức hình chiếu vuông góc.

Định lý 1(tọa độ hình chiếu vuông góc). Hình chiếu vuông góc của điểm $(x_0,y_0)$ lên đường thẳng $ax+by+c=0$ có tọa độ là

\[\Bigl{(}x_0-\frac{a(ax_0+by_0+c)}{a^2+b^2},y_0-\frac{b(ax_0+by_0+c)}{a^2+b^2}\Bigl{)}\]

 

Giao điểm của $\ell_1$ với $\ell_2$ là điểm $\Bigl{(}\dfrac{x_1+x_2}{2},x_1x_2\Bigl{)}$. Tương tự, ta có được tọa độ các đỉnh khác của tứ giác toàn phần. Qua một lượng các bước tính, ta thu được tọa độ của cực trực giao $P_1$ là

\[\Bigl{(}2x_2x_3x_4+\frac{x_2+x_3+x_4}{2}+\frac{2(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2},\frac{-1}{4}\Bigl{)}\]

Tiếp tục, ta tính được tọa độ của $X_1$ là

\[\Bigl{(}2x_2x_3x_4+\frac{x_2+x_3+x_4}{2}+\frac{2(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2},\]

\[4x_1x_2x_3x_4+x_1(-x_1+x_2+x_3+x_4)+\frac{4x_1(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2}\Bigl{)}\]

Tương tự, ta cũng thu được tọa độ của $X_2$, $X_3$ và $X_4$ vì sự bình đẳng của 4 cạnh của tứ giác toàn phần.

Bước cuối cùng là khó nhất, ta cần chứng minh 4 điểm trên đồng viên. Đây là một công việc có khối lượng tính toán hết sức khủng khiếp cho nên ta chỉ chứng minh một kết quả trung gian

_______________________________________________

Trong Oxy, cho 4 điểm $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$, $(x_4,y_4)$ mà 3 điểm bất kì trong số chúng đều không thẳng hảng. Câu hỏi đặt ra là tìm điều kiện để 4 điểm này đồng viên.

Vì $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$ không thẳng hàng nên sẽ có một đường tròn đi qua chúng, với phương trình có dạng $x^2+y^2+ax+by+c=0$. Điều kiện cần và đủ để 4 điểm đồng viên là tọa độ của cả 4 điểm phải thỏa mãn phương trình đó, tức là

\[(x_1^2+y_1^2)+ax_1+by_1+c=0\]

\[(x_2^2+y_2^2)+ax_2+by_2+c=0\]

\[(x_3^2+y_3^2)+ax_3+by_3+c=0\]

\[(x_4^2+y_4^2)+ax_4+by_4+c=0\]

Hệ nếu chỉ gồm 3 phương trình đầu thì chắc chắn có nghiệm $(a,b,c)$ nhưng nếu bổ sung phương trình thứ 4 thì chưa chắc. Vì vậy, để hệ 4 phương trình này có nghiệm thì phương trình thứ 4 phải là tổ hợp tuyến tính của 3 phương trình còn lại. Nói cách khác thì ta phải có định thức $4\times 4$ với 4 hàng  là $(1,1,1,1)$, $(x_1,x_2,x_3,x_4)$, $(y_1,y_2,y_3,y_4)$, $(x_1^2+y_1^2,x_2^2+y_2^2,x_3^2+y_3^2,x_4^2+y_4^2)$ phải bằng 0.

_______________________________________________

Chốt lại, "lời giải" trên chưa hoàn thiện :3

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 23-01-2017 - 10:41

[baopbc]

Link lời giải bài toán 141 :  http://artofproblems...1341458p7284966

[quanghung86]

Đúng vậy, cám ơn Bảo dẫn lại link, xin dịch lại lời giải của Telv Cohl như sau

 

Giải bài toán 141 (Telv Cohl). Gọi $ V_{ij} $ ($ i, $ $ j $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ i $ $ < $ $ j $ $ \leq $ $ 4 $) lần lượt là giao điểm của $ \ell_i, $ $ \ell_j $ và gọi $ T $ là hình chiếu của $ V_{23} $ trên $ \ell_4. $ Ta biết rằng $ H_k, $ $ P_k $ ($ k $ $ \in $ $ \mathbb{N}, $ $ 1 $ $ \leq $ $ k $ $ \leq $ $ 4 $) nằm trên đường thẳng Steiner của tứ giác toàn phần tạo bởi $ \ell_1, $ $ \ell_2, $ $ \ell_3, $ $ \ell_4, $ và chú ý rằng $ T $ $ \in $ $ \odot (H_1P_4X_4) $ nên ta thu được (từ định lý Reim's) $ H_1, $ $ H_2, $ $ V_{34} $ $ X_4 $ Đồng viên. Tương tự ta có thể chứng minh $ X_3 $ nằm trên đường tròn này và $ H_1, $ $ H_3, $ $ V_{24}, $ $ X_2, $ $ X_4 $ cũng đồng viên, do đó ta thu được

 

$$ \measuredangle X_2X_4X_3 = \measuredangle X_2X_4H_1 + \measuredangle H_1X_4X_3 = \measuredangle X_2V_{24}H_1 + \measuredangle H_1V_{34}X_3 = \measuredangle (\ell_2, \perp \ell_3) + \measuredangle (\perp \ell_2, \ell_3). $$

 

Tương tự, ta có $ \measuredangle X_2X_1X_3 $ $ = $ $ \measuredangle (\ell_2, \perp \ell_3) $ $ + $ $ \measuredangle (\perp \ell_2, \ell_3), $ do đó chúng ta thấy rằng $ X_1, $ $ X_2, $ $ X_3, $ $ X_4 $ đồng viên.

 

Mình xin đề nghị bài tiếp cho topic tiếp tục.

 

Bài toán 142. Cho hình chữ nhật $ABCD$ và $P$ nằm trên cạnh $AB$. $Q,R$ đối xứng với $A,B$ qua $P$. Trung trực $PC,PD$ lần lượt cắt $BC,AD$ tại $M,N$. $MQ$ cắt $NR$ tại $X$. Chứng minh rằng đường tròn $(X,XP)$ tiếp xúc $CD$.

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 23-01-2017 - 13:56
Chỉnh đề

[quanghung86]

Vừa rồi kết quả VMO khá khả quan với một số thành viên của diễn đàn, mình xin gửi lời chúc mừng tới các bạn. Để đầy mạnh phong trào đồng thời cũng có ý nghĩa cho việc chuẩn bị vòng 2, mình xin mạn phép đầy nhanh tốc độ Marathon bằng cách đề nghị song song thêm 2-3 bài toán, ai giải xong bài nào cứ tiếp tục đề nghị số thứ tự tiếp tục, làm thế để tăng số lượng bài và tăng hiệu suất làm việc, mong các bạn khi giải xong đề nghị các bài toán mới sát với vòng 2 để chúng ta cùng ôn tập luôn. Chúng ta vẫn duy trì quy tắc sau 2 ngày nếu chưa ai giải thì người đề nghị post đáp án !

 

Bài toán 143 (Tập huấn IMO 2013). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $P$ là điểm bất kỳ. Đường thẳng qua $P$ vuông góc với $BC$ cắt $CA,AB$ tại $A_1,A_2$. Gọi $(K_a)$ là đường tròn ngoại tiếp tam giác $AA_1A_2$. Tương tự có $(K_b),(K_c)$. Gọi $(K)$ là đường tròn tiếp xúc trong với $(K_a),(K_b),(K_c)$. Gọi $(L)$ là đường tròn tiếp xúc ngoài với $(K_a),(K_b),(K_c)$. Chứng minh rằng các đường tròn $(O),(K),(L)$ đồng trục.

[quanghung86]

Qua hai ngày mình xin post đáp án bài toán 142.

 

 

Giải bài toán 142. Gọi $H$ là hình chiếu của $P$ lên $CD$. Cho $H(0,0),C(c,0),D(d,0),P(0,p)$ thì $A(d,p),B(c,p),Q(-d,p),R(-c,p),M(c,\frac{c^2+p^2}{2p}),N(d,\frac{d^2+p^2}{2p})$. Ta tính được tọa độ $X(-\frac{cd+p^2}{c+d},\frac{p^4+p^2(c^2+d^2+4cd)+c^2d^2}{2p(c+d)^2}).$

 

Từ đó $d(X,CD)=\frac{p^4+p^2(c^2+d^2+4cd)+c^2d^2}{2p(c+d)^2}$ và như vậy

 

$$XP^2=(\frac{p^2+cd}{c+d})^2+(\frac{p^4+p^2(c^2+d^2+4cd)+c^2d^2}{2p(c+d)^2}-p)^2=(\frac{p^4+p^2(c^2+d^2+4cd)+c^2d^2}{2p(c+d)^2})^2=d(X,CD)^2.$$

 

Bài này dùng tọa độ theo mình là tối ưu, bạn nào có lời giải thuần túy hình hãy đóng góp tiếp

[quanghung86]

Mình xin đề nghị bài toán tiếp

 

Bài toán 144. Cho tam giác $ABC$ với đường cao $AD,BE,CF$. Chứng minh rằng điểm Lemoine của tam giác $ABC$ là trọng tâm tam giác tạo bởi các điểm Lemoine của tam giác $AEF,BFD,CDE$.

[Min Nq]

Lời giải bài 144

 

Gọi $L_1, L_2, L_3$ là điểm Lemoine các tam giác $AEF,BDF,EDC$

 

Để ý rằng $EF=a cosA$, $AE=c cos A$, $AF=b cosA$ và các đẳng thức tương tự, ta có các đẳng thức vector sau:

 

$a^{2}\vec{LA}+b^{2}\vec{LB}+c^{2}\vec{LC}=0$

$a^{2}\vec{L_{1}A}+b^{2}\vec{L_{1}E}+c^{2}\vec{L_{1}F}=0$

$a^{2}\vec{L_{2}D}+b^{2}\vec{L_{2}B}+c^{2}\vec{L_{2}F}=0$

$a^{2}\vec{L_{1}D}+b^{2}\vec{L_{1}E}+c^{2}\vec{L_{1}C}=0$

 

Suy ra

 

$(a^2+b^2+c^2)(\vec{LL_{1}}+\vec{LL_{2}}+\vec{LL_{3}})+(a^2\vec{LA}+b^2\vec{LE}+c^2\vec{LF})+(a^2\vec{LD}+b^2\vec{LB}+c^2\vec{LF})+(a^2\vec{LD}+b^2\vec{LE}+c^2\vec{LC})=0$

 

Vậy ta cần chứng minh:

 

$a^2\vec{LD}+b^2\vec{LE}+c^2\vec{LF}=0$

hay

$a^2\vec{AD}+b^2\vec{BE}+c^2\vec{CF}=0$

 

Đẳng thức này đúng nên $\vec{L_{1}L}+\vec{L_{2}L}+\vec{L_{3}L}=0$

 

Ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi Min Nq: 26-01-2017 - 11:06

[QuangDuong12011998]

Em đăng lời giải cho bài 143.
$O_a$ là tâm ngoại tiếp tam giác $AA_1A_2$.
Như vậy $AO_a$ và đường thẳng qua $A$ và song song $BC$ đẳng giác với góc $BAC$. Vậy $AO_a$ là tiếp tuyến của $(ABC)$ nên $(O)$ trực giao với $(AA_1A_2)$. Tương tự $(O)$ trực giao với $(BB_1B_2)$ và $(CC_1C_2)$. Do đó $(K)$ và $(L)$ là nghịch đảo của nhau qua phép nghịch đảo đường tròn $(O)$, điều đó dẫn đến $(O)$, $(K)$, $(L)$ đồng trục.

[quanghung86]

Cám ơn em, xin dịch lại lời giải của bạn Đỗ Xuân Long đưa ra tại đây

 

Gọi $X,Y,Z$ là điểm Lemoine của các tam giác $AEF,BDF,CDE$. $H,O,G,L$ là trực tâm, tâm ngoại tiếp, trọng tâm, điểm Lemoine của tam giác $ABC$. $M, N$ là trung điểm của $BC, EF$. $T$ là trung điểm $AD$. $AU\perp EF$. $V$ là trung điểm $AU$. ta biết rằng $MT$ đi qua $L$. Từ $AU\parallel MN$, ta có $\frac {XA}{XM}=\frac {XV}{XN}=\frac {LT}{LM}$ vì vậy nên $XL\parallel AH \implies XL\perp BC$. Từ $\triangle DYZ\sim \triangle HBC$, ta thấy $AM\perp YZ \implies GX\perp YZ$. Gọi $\ell$ là đường thẳng qua $X$ và song song $YZ$. $t$ là đường thẳng qua $G$ và vuông góc $AD.$ Ta có $X(L,\ell,Y,Z)=G(M,t,BC)=-1$, nên $XL$ chia đôi $YZ$. Tương tự thì $L$ là trọng tâm tam giác $XYZ$.

 

Mình xin đề nghị bài tiếp.

 

Bài toán 145 (AoPS). Cho tam giác $ABC$ với $\angle BAC<45^{\circ}$. $D$ ở trong tam giác $ABC$ sao cho $BD=CD$ và $\angle BDC=4\angle BAC$. $E$ là đối xứng của $C$ qua $AB$. $F$ là đối xứng của $B$ qua $AC$. Chứng minh rằng $AD\perp EF$.

 

 

[Nguyen Dinh Hoang]

1 Lời giải thuần túy khác cho bài 143

 

Bổ đề: Cho tam giác $ABC$, trực tâm $H$, đường cao $AD$,$BE$, $CF$. $M$, $N$ lần lượt là điểm $Lemoine$ của các tam giác $BFD$, $CDE$. $I$ là trung điểm $BC$. Khi đó $MN$ vuông góc $AI$

Chứng minh:

Gọi $Q$ là giao của $EF$ và $BC$. $S$ là giao của $QH$ với $BFD$ tương tự gọi $T$. Ta có $QH$ vuông góc $AI$. Ta chứng minh $S$, $M$, $D$ thẳng hàng. Thật vậy ta có $\measuredangle MDB = \measuredangle IAC$ do đồng dạng mà $\measuredangle SDB = \measuredangle QHB = \measuredangle IAC$ nên $S$, $M$, $D$ thẳng hàng. Tương tự ta có $D,N,T$ thẳng hàng và do $DBS$ đồng dang $DET$ và $DBM$ đồng dạng $DEN$ nên $MN // ST$  nên $MN$ vuông góc $AI$

Trở lại bài toán.

Gọi $X, Y, Z$ thứ tự là điểm $Lemoine$ của $AEF$, $BCF$, $CDE$ ta có kết quả sau $XL$ vuông góc $BC$ nên Áp dụng tính chất hàng điểm vuông góc ta có $X(LYZx)$ mà Xx là đường qua $X$ và song song $YZ$ chuyển thành $A(BCIy)$ trong đó $Ay$ là đường qua $A$ song song $BC$ hàng này điều hòa nên ta có $dpcm$

Bài viết đã được chỉnh sửa nội dung bởi Nguyen Dinh Hoang: 26-01-2017 - 11:34

[quanghung86]

Cám ơn Dương lời giải của em cũng tương tự lời giải của Luis đưa ra ở đây nên thầy không dịch lại lời giải trong link nữa. Xin đề nghị bài tập tiếp

 

Bài toán 146. Cho tam giác $ABC$ với trực tâm $H$. $D$ là điểm nằm cũng phía $A$ với $BC$. $E,F$ thuộc cạnh $CA,AB$ sao cho $\angle HEC=\angle DCB$ và $\angle HFB=\angle DBC$. $M,N$ là đối xứng của $E,F$ qua $HC,HB$. Đường tròn $(HCM)$ và $(HBN)$ cắt nhau tại $K$ khác $H$. $L$ là tâm ngoại tiếp của tam giác $HEF$. Chứng minh rằng $HL\parallel KD$.

 

Bài viết đã được chỉnh sửa nội dung bởi quanghung86: 26-01-2017 - 17:41