ĐỀ THI TUYỂN SINH
VÀO KHỐI TRUNG HỌC PHỔ THÔNG CHUYÊN ĐH SƯ PHẠM 2016-2017
Môn thi: Toán học
(Dùng cho thí sinh thi vào Chuyên Toán và Chuyên Tin)
Thời gian làm bài:150 phút
Câu 1: (1,5 điểm) Chứng minh biểu thức sau nhận giá trị nguyên dương với mọi giá trị nguyên dương của $n$:
$$P=\left ( \sqrt{n^2+\left ( n+1 \right )^2}+\sqrt{\left ( n-1 \right )^2+n^2} \right )\sqrt{4n^2+2-2\sqrt{4n^4+1}}$$
Câu 2 (2,5 điểm)
a)Tìm số nguyên dương $x,y$ thỏa mãn : $x^3-y^3=95(x^2+y^2)$
b)Tìm các số thực $x,y$ thỏa mãn:
$$\frac{x^2-4}{x}+\frac{y^2-4}{y}+8=4\left ( \sqrt{x-1}+\sqrt{y-1} \right )$$
Câu 3 (2,0 điểm) Cho $S$ là tập hợp các số nguyên dương $n$ có dạng $n=x^2+3y^2$ trong đó $x,y$ là các số nguyên dương.Chứng minh rằng:
a)Nếu $a,b \in S$ thì $ab \in S$
b)Nếu $N \in S$ và $N$ chẵn thì $N$ chia hết cho $4$ và $\frac{N}{4} \in S$
Câu 4 (3,0 điểm)
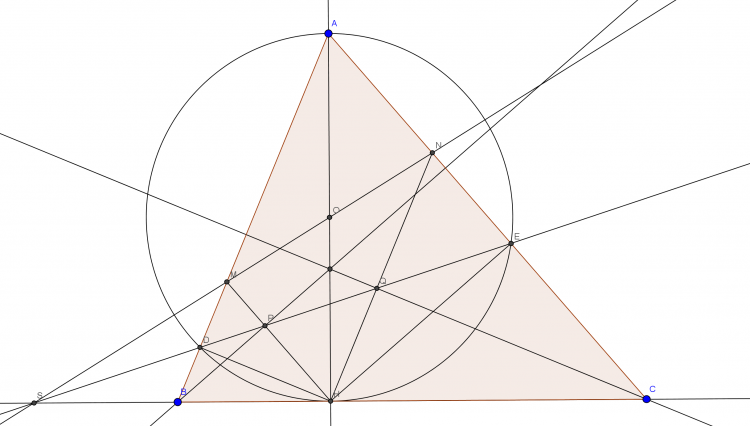
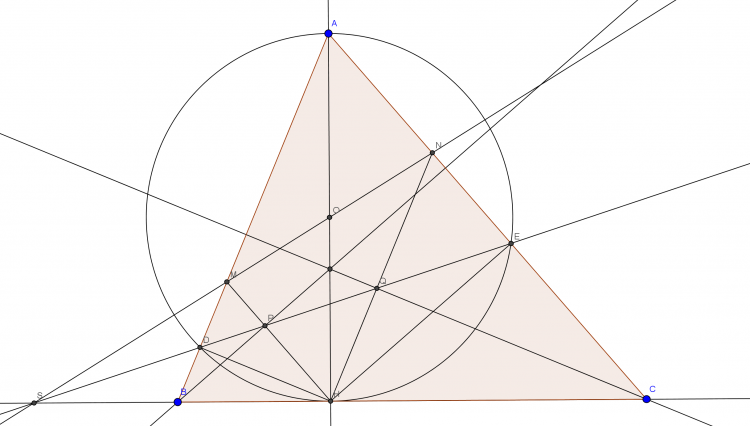
Cho tam giác $ABC$ nhọn $AB<AC$ . Kẻ đường cao $ẠH$ . Đường tròn $(O)$ đường kính $AH$ cắt cạnh $AB,AC$ tương ứng tại $D,E$ .Đường thẳng $DE$ cắt đường thẳng $BC$ tại $S$
a)Chứng minh rằng $BDEC$ là tứ giác nội tiếp
b)Chứng minh rằng $SB.SC=SH^2$
c)Đường thẳng $SO$ cắt $AB,AC$ tương ứng tại $M,N$ đường thẳng $DE$ cắt $HM,HN$ tương ứng tại $P,Q$ .Chứng minh rằng: $BP , CQ$ và $AH$ đồng quy
Câu 5 (1,0 điểm) Giả sử mỗi điểm của mặt phẳng được tô bởi một trong ba màu : xanh,đỏ,vàng . Chứng minh rằng tồn tại ba điểm cùng màu là ba đỉnh của một tam giác cân
HẾT
Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 03-06-2016 - 16:56