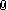 triangle.png
triangle.png
Đường thẳng qua $H$ song song với $AC$ cắt $AB$ tại $M'$, đường thẳng qua $H$ song song với $AB$ cắt $AC$ tại $N'$. Từ đó, ta có $AM'HN'$ là hình bình hành $\Rightarrow$ $M'$,$O$,$N'$ thẳng hàng. $(1)$
Theo định lí Menelaus cho 3 điểm $S$,$D$,$E$ của $\Delta ABC$, ta có:
$\frac{SB}{SC}.\frac{EC}{EA}.\frac{DA}{DB}=1$.
Lại có $\frac{EC}{EA}=\frac{HC^{2}}{HA^{2}}$ và $\frac{DA}{DB}=\frac{HA^{2}}{HB^{2}}$ nên $\frac{SB}{SC}.\frac{HC^{2}}{HB^{2}}=1$. Mặt khác, theo định lí $Thales$, ta có $\frac{HC}{HB}=\frac{M'A}{M'B}=\frac{N'C}{N'A}$ nên ta có $\frac{SB}{SC}.\frac{M'A}{M'B}.\frac{N'C}{N'A}=1$. Do đó, theo định lí Menelaus đảo, ta có ba điểm $S$,$M'$,$N'$. $(2)$.
Từ $(1)$ và $(2)$, ta có $S,M',O,N'$ thẳng hàng nên $M\equiv M'$ và $N\equiv N'$. Từ đó, ta sẽ chứng minh được các tứ giác $BDPH$ và $CEQH$ nội tiếp. Suy ra $BP$ và $CQ$ lần lượt là hai đường cao của $\Delta ABC$. Nên $BP,CQ,AH$ đồng qui.
Có thể chứng minh như sau:
a. Ta có HDAE nội tiếp => $\angle ADE=\angle AHE = \angle ACB$ => đpcm
b. Từ câu a => $SB.SC=SD.SE=SH^2$ ($SH$ là tiếp tuyến của $(ADH)$)
c. Xét tam giác AHC, kẻ HN'//MN cắt AC tại N' ta dễ chứng minh $\frac{AN}{NC}=\frac{SH}{SC}$ (1)
Mà theo câu b ta có $SB.SC=SH^2$ <=> $SC.SB=SH.SC-SH^2$ <=> $SC.HB=SH.HC$ <=> $\frac{HB}{HC}=\frac{SH}{SC}$ (2)
(1), (2) => $\frac{AN}{NC}=\frac{HB}{HC}$ => $HN//AB$
Tương tự ta cũng chứng minh được: $MH//AC$
=> $\angle BHM + \angle EHC = \angle BCA + \angle EHC = 90^0$ => MH vuông góc với HE, tương tự NH vuông góc với HD
BDPH nội tiếp => BP vuông góc với MN => BP là đường cao, tương tự CQ là đường cao => đpcm.
triangle.png








