Chủ đề này có 23 trả lời

[baopbc]

Lời giải bài tổng quát của em!

Lời giải. 

$P'\equiv BP\cap CQ,Q'=BQ\cap CP$. Dễ thấy $E,F,G,H$ cùng thuộc một đường tròn. Do $\angle BP'C=180^\circ-\angle P'CB-\angle P'BC=180^\circ-\angle PCE-\angle EPC=\angle PEC\Longrightarrow P,P',E,C$ cùng thuộc một đường tròn $\Longrightarrow \angle EP'C=\angle EPC=\angle P'BC\Longrightarrow P'E$ là tiếp tuyến tại $P'$ của $(P'BC)$. Tương tự thì $H,Q,P'B$ cùng thuộc một đường tròn nên $P'H$ là tiếp tuyến tại $P'$ của $(BP'C)\Longrightarrow E,P',H$ thẳng hàng.

Tương tự ta cũng có $F,Q',G$ thẳng hàng.

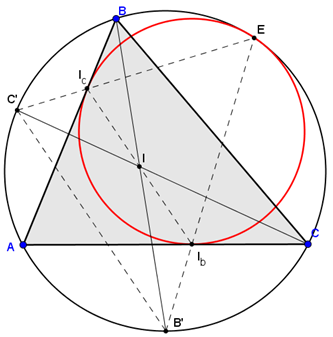
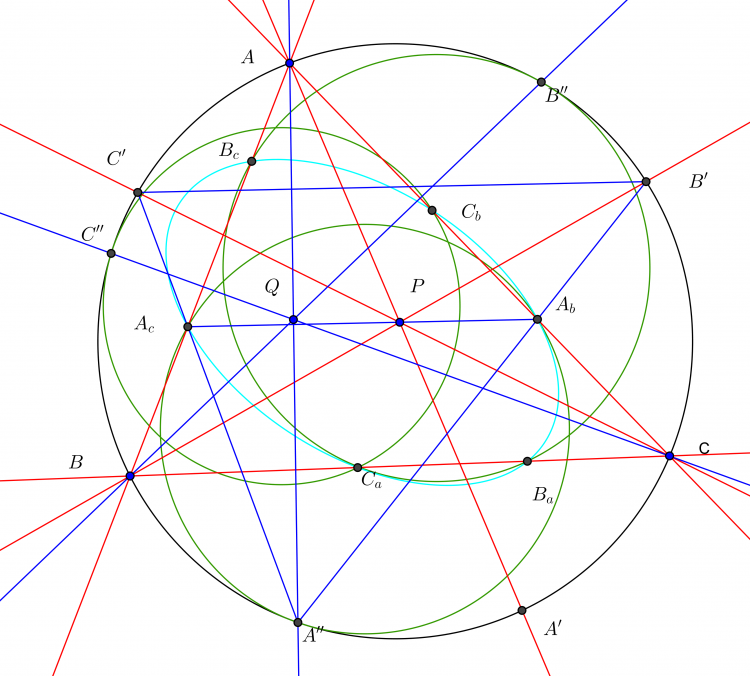
Hình vẽ bài toán tổng quát

Đường tròn ngoại tiếp các tam giác $Q'FB$ và $Q'GC$ cắt nhau tại $M$. Do $F,Q',G$ thẳng hàng nên $M$ thuộc $(ABC)$.

Do $F,Q',P,B$ và $G,Q,Q'C$ cùng thuộc một đường tròn nên $M$ thuộc $(QGC)$ và $(PFB)$. Mặt khác do $M$ thuộc $(ABC)$ nên $M\equiv \odot (PFB)\cap \odot (PEC) \equiv \odot (QHB)\cap (QGC)$. Theo kết quả quen thuộc thì $(MHG),(MEF)$ tiếp xúc $(O)$.

Mặt khác $\angle EMF=\angle EMP+\angle FMP=\angle BP'H+\angle BPH=180^\circ-\angle EMF\Longrightarrow F,H,E,M$ cùng thuộc một đường tròn

$\Longrightarrow (HGEF)$ tiếp xúc $(O)$ tại $M.\blacksquare$

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 07-06-2016 - 12:30

[quanghung86]

Quay lại bài toán ban đầu, có một mở rộng rất thú vị sang hình chữ nhật như sau

 

Cho hình chữ nhật $ABCD$ nội tiếp đường tròn $(O)$ và $P$ thuộc cung $AD$ không chứa $B,C$. Trung trực $MA,ND$ cắt $BD,CA$ tại $S,T$. Trung trực $MA,ND$ cắt $PB,PC$ tại $Q,R$. $K$ là trung điểm $S,T$. Chứng minh rằng đường tròn $(K )$ đi qua $Q,R$ tiếp xúc $(O)$.

Hình gửi kèm

• 

[Ngockhanh99k48]

Theo em thấy thì ý tưởng của các lời giải trên có thể chứng minh bài này.
Dễ thấy $Q, R$ là trung điểm $BM, CN$, nên $Q, O, R$ thẳng hàng và là trục đối xứng của hình chữ nhật $ABCD$. $AQ$ cắt $DR$ tại $X$. $SQ, TR$ thứ tự cắt $AC, BD$ tại $Y, Z$ thì $Q, R$ thứ tự là trung điểm $SY, TZ$. Do đó $QK \parallel AC$ và $RK \parallel BD$ do đó $\widehat{QKR}=\widehat{AOD}=\widehat{AXD}=\widehat{QXR}$. Hơn nữa $SQRT$ là hình thang vuông nên dễ thấy $\triangle QKR$ cân tại $K$. Do đó ta có ngay $K$ là tâm của đường tròn $(XQR)$. $AQ, DR$ thứ tự cắt $BC$ tại $E, F$. Dễ thấy $DCFN$ là hình chữ nhật nên $TZ$ cũng là trung trực $CF$. Do đó $\triangle TCF$ cân tại $T$. Hay ta có $TF \parallel BD$. Tương tự $SE \parallel AC$. Nếu $SE$ cắt $TF$ tại $H$ thì ta cũng suy ra $H$ là tâm ngoại tiếp $\triangle XEF$. Do $EF \parallel QR$ nên $X, H, K$ thẳng hàng. Mặt khác $SHTO$ là hình bình hành nên $H, K, O$ thẳng hàng. Do đó $O, K, X$ thẳng hàng. Ta có đpcm.

[Oai Thanh Dao]

Hôm qua mình có trao đổi với một cậu nước ngoại tại đây:

https://groups.yahoo...s/messages/3329

Cậu ấy viết:

Dear friends,
Consider a triangle ABC. Let I be the incenter of ABC. Draw CI such that meet the circumcircle of ABC at C’. Similarly, construct the point B’. Now, draw a line paralell to B’C’ passing throu I, such that intersect AB in I_c and AC in I_b. The lines B’I_b, C’I_c intersect at a point, E, on the circumcircle of ABC. Then, the circumcircle of triangle I_bI_cE is a mixtilinear incircle. See image attached.

I want to know whether this construction is new or not. Thanks in advance.

Best regards,
Emmanuel.



Và tìm ra một mở rộng tại đây: https://groups.yahoo...s/messages/3330


Dear Emmanuel José García, Dear Geometers,

I inspired from your construct. I posed a generalization of Mixtilinear circle as follows:

Let ABC be a triangle, P be a point on the plane, let A'B'C' be the circumcevian of P. Let a line through P and parallel to B'C', the line meets AC, AB at Ab, Ac respectively. Then B'Ab meets C'Ac at a point A'', and circle (AbAcA'') tangent with the circumcircle at A''. Define Bc, Ba, Ca, Cb cyclically , and Define B'', C'' cyclically. Then show that:

1. AA'', BB'', CC'' are concurrent.
2. Six points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic



Best regards
Sincerely
Dao Thanh Oai


Tuy nhiên kết quả trên về bản chất sẽ trùng với ý tưởng của Bảo. Mình đã xác nhận tại diễn đàn đó là tuy lấy cảm hứng từ bài của Emmanuel để đưa ra mở rộng của đường tròn Mixtilinear. Nhưng kết quả này được tổng quát hóa trước đó bởi Bảo. Về mặt khoa học như thế coi như đã xác nhận kết quả này không phải của mình mà là của Bảo.

Bài viết đã được chỉnh sửa nội dung bởi Oai Thanh Dao: 18-07-2016 - 09:47