Chủ đề này có 23 trả lời

[baopbc]

Như vậy thầy Hùng đã đưa ra lời giải bài cũ trong tuần 2 tháng 6 và kèm theo đó là bài toán mới:

 

Bài 42. Cho hình vuông $ABCD$ nội tiếp trong đường tròn $(O).P$ là một điểm thuộc cung nhỏ $AD$ của $(O).PB,PC$ lần lượt cắt đoạn $AD$ tại $M,N$. Trung trực của $AM,DN$ lần lượt cắt $BD,CA$ tại $S,T.ST$ cắt $PB,PC$ lần lượt tại $U,V$. Chứng minh rằng đường tròn đường kính $UV$ tiếp xúc $(O)$.

Hình vẽ bài toán

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 05-06-2016 - 20:34

[Nguyen Dinh Hoang]

Lời giải. $H\equiv AP\cap $ trung trực $DM$. Tương tự có $K\Longrightarrow DH$ và $KL$ cắt nhau tại $Q$ thuộc $(O)$.  Ta có $H,O,K$ thẳng hàng. $I\equiv DO\cap AH,J\equiv IK\cap OC$. Ta có $\triangle IDM$ cân tại $I$ và $\widehat{IDM}=45^\circ\Longrightarrow IM\perp DO\Longrightarrow IM\parallel AC$. Tương tự $NJ\parallel DB$.

Theo Thales thì $IM,JN$ cắt nhau tại một điểm thuộc $OP\Longrightarrow OP$ chia đôi $IJ$.

Theo tính chất đối xứng thì $OQ$ chia đôi $ST\Longrightarrow \widehat{AOQ}=\widehat{DOP}$ (do $HOPD$ là tứ giác nội tiếp) $\Longrightarrow \widehat{DOP}=\widehat{DHP}=2\widehat{DAP}=2\widehat{APQ}=\widehat{AOQ} \Longrightarrow OP\perp ST\Longrightarrow OP\perp UV\Longrightarrow \widehat{DOP}=\widehat{VHQ}$.

$X\equiv DH\cap AO\Longrightarrow VSXH$ là tứ giác nội tiếp $\Longrightarrow VX\perp BP,UY\perp PA$.

$\Longrightarrow H,V,Q,U,R$ đồng viên. Mặt khác ta có $OQ$ đi qua trung điểm $ST$.

Ta sẽ chứng minh $VS=TU$. Thật vậy vì $SV=SX,\frac{SX}{AX}=\frac{SH}{AD}=\frac{HO}{AD}$.

Lại có $TU=TY$ và $\frac{TY}{BY}=\frac{TK}{BC}=\frac{DK}{BC}$ (theo tính chất đối xứng) $\Longrightarrow HO.AX=OK.BY\Longrightarrow SV=TU\Longrightarrow OQ$ chia đôi $UV$

$\Longrightarrow OQ$ đi qua tâm $(UV)$.

$\Longrightarrow (UV)$ tiếp xúc $(O).\blacksquare$

Bài viết đã được chỉnh sửa nội dung bởi Nguyen Dinh Hoang: 05-06-2016 - 21:05

[baopbc]

Lời giải của em không được đẹp lắm!

Lời giải. Đường thẳng qua $O$ song song với $AB$ cắt $PA,PB$ lần lượt tại $X,Y$. Do $O$ là trung điểm $AC$ nên $X$ là trung điểm $AM\Longrightarrow X$ thuộc trung trực $DM\Longrightarrow SX\perp CD\Longrightarrow SX\perp OX$. Tương tự thì $OY\perp YT$.

 

 

Áp dụng định lí $Sin$ cho các tam giác $XOA$ và $YOB$ ta được:

 

$\frac{OX}{OA}=\frac{\sin\measuredangle XAO}{\sin\measuredangle XAO}=\frac{\sin(90^\circ-\measuredangle B)}{\sin \measuredangle C}=\frac{\cos \measuredangle B}{\sin \measuredangle C}$.

 

Tương tự thì $\frac{OY}{OB}=\frac{\cos\measuredangle C}{\sin \measuredangle B}\Longrightarrow \frac{OX}{OY}=\frac{\cos \measuredangle B.\sin \measuredangle B}{\cos \measuredangle B.\sin \measuredangle C}=\frac{\sin 2\measuredangle B}{\sin 2\measuredangle C}$

 

$\Longrightarrow \frac{\sin \measuredangle OTS}{\sin \measuredangle OST}=\frac{\sin (2\measuredangle B-90^\circ)}{\sin (2\measuredangle C-90^\circ)}$

 

Mặt khác do $2\measuredangle B+2\measuredangle C-90^\circ-90^\circ=90^\circ$ nên theo định lí hàm số $Sin$ ta suy ra $\measuredangle OST=2\measuredangle B-90^\circ,\measuredangle OTS=2\measuredangle C-90^\circ$

$\Longrightarrow \measuredangle XUS=\measuredangle OST+\measuredangle OAP=2\measuredangle B-90^\circ+90^\circ-\measuredangle B=\measuredangle B$

Tương tự ta suy ra $X,Y,V,U$ cùng thuộc một đường tròn $\Longrightarrow PO\perp ST$.

$Z\equiv PO\cap ST\Longrightarrow X,O,Z,S$ cùng thuộc một đường tròn $\Longrightarrow \measuredangle XZV=135^\circ\Longrightarrow P,X,Z,V$ cùng thuộc một đường tròn.

$\Longrightarrow \measuredangle VXP=90^\circ$.

Tương tự thì $\measuredangle UYP=90^\circ$.

Lấy $Q$ đối xứng $P$ qua $XY$. Hiển nhiên $Q$ thuộc $(O)$. Do $\measuredangle XQY=45^\circ=\measuredangle XVY$ nên $Q$ thuộc $(UV)$

Mặt khác do $(QXY)$ tiếp xúc $(O)$ nên $(UV)$ tiếp xúc $(O).\square$

 

 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 05-06-2016 - 20:37

[baopbc]

Một hướng tổng quát cho bài toán:

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, trực tâm $H$. Đường thẳng qua $H$ vuông góc với $AO$ cắt $CA,AB$ tại $E,F$. Đường thẳng qua $O$ song song với $BC$ cắt $CA,AB$ lần lượt tại $P,Q$. Chứng minh rằng đường tròn đi qua $4$ điểm $P,Q,E,F$ tiếp xúc đường tròn $(O)$.

Hình vẽ

[baopbc]

Tổng quát hơn nữa thu được một kết quả ấn tượng!

Cho tam giác $ABC.P,Q$ là hai điểm liên hợp đẳng giác. Tiếp tuyến tại $P$ của đường tròn ngoại tiếp tam giác $BPC$ cắt $CA,AB$ lần lượt tại $E,F$. Giả sử tồn tại một đường thẳng qua $Q$ cắt $CA,AB$ tại $G,H$ sao cho $E,F,G,H$ cùng thuộc một đường tròn. Chứng minh rằng đường tròn đi qua bốn điểm $E,F,G,H$ tiếp xúc $(ABC)$.

Hình vẽ bài toán

[quanghung86]

Cám ơn các em về lời giải và các tổng quát rất ý nghĩa của Bảo, thầy cũng xuất phát từ một bài tổng quát đi tới bài này, tuy nhiên thực sự là việc ghép nó vào một hình vuông nội tiếp là kết quả đẹp !

[QuangDuong12011998]

Cặp điểm đẳng giác luôn rất thu hút. Phải đăng nhập để like cho Bảo!

Lời giải của mình.

$QB$, $QC$ cắt $(ABC)$ tại $Y$, $Z$.

$GY$ cắt $HZ$ tại $T$ thì theo định lý Pascal đảo, $T$ thuộc $(ABC)$.

Cộng góc

\[(HG,YZ)=(HG,HA)+(AB,AZ)+(ZA,ZY)=(HG,HF)+(CB,CQ)+(BA,BQ)\]

\[=(EG,EF)+(CP,CA)+(BP,BC)=(AC,PP)+(CP,CA)+(BP,BC)\]

\[=(AC,PP)+(CP,CA)+(BP,BC)=(PC,PP)+(BP,BC)=0\]

trong đó $PP$ là tiếp tuyến tại $P$ của $(PBC)$

Suy ra $GH$ song song $YZ$, theo đó, $(TGH)$ tiếp xúc $(TYZ)$ nên $(TGH)$ tiếp xúc $(ABC)$.

Hình gửi kèm

• 

[babystudymaths]

Mọi người giải nhanh quá. Em xin đóng góp thêm một lời giải khác cho bài toán gốc.

Qua $O$ kẻ đường thẳng song song $AD$, cắt $BM, CN$  lần lượt tại $E, F$.

Từ đó suy ra $EB=EM=EA, FC=FN=FD \Rightarrow SE\perp AB, TF\perp AB\Rightarrow SE\parallel AB, TF\parallel CD$

Lấy $L$ đối xứng $P$ qua $EF$ thì $L\in (O)$ . Do tính đối xứng nên $\overline{A, E, L}  và  \overline{D, F, L}$ .

Lấy $J$ là trung điểm $ST\Rightarrow JS=JT=JO$.

Mặt khác $\widehat{ESO}=\widehat{EOS}=45^\circ, \widehat{FTO}=\widehat{FOT}=45^\circ\Rightarrow ES=EO, FT=FO$

$\Rightarrow JE\perp SO, JF\perp TO\Rightarrow JE\perp JF.$. Mà$\widehat{JEF}=\widehat{JFE}=45^\circ$

$\Rightarrow JE=JF$.

Mặt khác $\widehat{ELF}= 45^\circ=\frac{1}{2} \widehat{EJF}\Rightarrow JL= JE= JF\Rightarrow L, J, O$  thẳng hàng ( vị tự ).

Mà $\widehat{UEL}=2 \widehat{BAL}=\widehat{BOL}= \frac{1}{2} \widehat{UJL}\Rightarrow U\in (J,JE)\Rightarrow JU= JL$

Tương tự $JL=JV\Rightarrow L\in (UV)$ 

Rõ ràng, ta suy ra $(UV)$ tiếp xúc $(O).\blacksquare$

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 06-06-2016 - 10:17
$\LaTeX$

[QuangDuong12011998]

Xin lỗi thầy và các bạn, lời giải cho bài toán tổng quát ở trên chưa được hoàn chỉnh, hic. Do chưa chỉ ra $T,G,H,E,F$ đồng viên.

Continue:

$QQ$ là tiếp tuyến tại $Q$ của $(QBC)$

\[(CA,GH)=(PP,AB)=(PP,PB)+(PB,BA)=(CP,CB)+(BP,BA)\]

\[=(CA,CQ)+(BC,BQ)=(CA,CQ)+(CQ,QQ)=(CA,QQ)\]

$\Rightarrow$ $GH$ tiếp xúc $(QBC)$ tại $Q$.

$(TGH)$ cắt $AC$, $AB$ tại $E'$, $F'$ khác $G$, $H$. $TE'$, $TF'$ cắt $(ABC)$ tại $M$, $N$.

Bổ đề. $\triangle ABC$, $M$, $N$ thuộc $BC$ thì $(AMN)$ tiếp xúc $(ABC)$ khi và chỉ khi $AM$, $AN$ đẳng giác với góc $A$.

Chứng minh bổ đề: $O$, $I$ là tâm của $(ABC)$ và $(AMN)$, $AH$ là đường cao của $\triangle ABC$ thì đương nhiên $AH$ cũng là đường cao của $\triangle AMN$. $AH$, $AO$ đẳng giác với $\angle (AB,AC)$; $AH$, $AI$ đẳng giác với $\angle (AM,AN)$ nên $(A,O,I)$ thẳng hàng khi và chỉ khi $\angle(AB,AC)$ và $\angle (AM,AN)$ có chung phân giác - tức là $AM$, $AN$ đẳng giác.

Quay lại bài toán.

Do đã có $(TGH)$ tiếp xúc $(ABC)$ tại $T$ nên theo bổ đề: $TM$, $TY$ đẳng giác với $\angle (TA,TC)$; $TN$, $TZ$ đẳng giác với $\angle (TA,TB)$.

$\Rightarrow$ $MY$ song song $CA$, $NZ$ song song $AB$. Điều này nghĩa là $BM$, $BY$ đẳng giác với $\angle(BA,BC)$ và $CN$, $CZ$ đẳng giác với $\angle (CA,CB)$(cung chứa góc). Do đó $BM$, $CN$ đi qua $P$.

Tương tự như chứng minh $YZ$ song song $GH$ ở trên, ta có thể chỉ ra $EF$ song song $MN$.

Mà theo định lý Pascal, $E'$, $P$, $F'$ thẳng hàng. $T$ là tâm vị tự của $(TGHE'F')$ và $(ABC)$ nên

\[\dfrac{\overline{TF'}}{\overline{TN}}=\dfrac{\overline{TH}}{\overline{TZ}}=\dfrac{\overline{TG}}{\overline{TY}}=\dfrac{\overline{TE'}}{\overline{TM}}\]

theo định lý Thales đảo, $E'F'$ song song $MN$.

Như vậy $EF$, $E'F'$ đều đi qua $P$ và song song $MN$ nên kết luân $E'=E$, $F'=F$

Vậy $(EFGH)$ tiếp xúc $(ABC)$.

P.S: Tổng quát của Bảo cũng là mở rộng đường tròn mixtilinear. Sẽ đẹp hơn nếu phát biểu lại như sau: tiếp tuyến tại $P$ của $(PBC)$ cắt $AC,AB$ tại $E$, $F$; tiếp tuyến tại $Q$ của $(QBC)$ cắt $AC,AB$ tại $G$, $H$ thì $E,F,G,H$ cùng thuộc một đường tròn tiếp xúc $(ABC)$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi QuangDuong12011998: 06-06-2016 - 09:08

[quanghung86]

Mọi người giải nhanh quá. Em xin đóng góp thêm một lời giải khác cho bài toán gốc.

geogebra-export (3).png

Qua $O$ kẻ đường thẳng song song $AD$, cắt $BM, CN$  lần lượt tại $E, F$.

Từ đó suy ra $EB=EM=EA, FC=FN=FD \Rightarrow SE\perp AB, TF\perp AB\Rightarrow SE\parallel AB, TF\parallel CD$

Lấy $L$ đối xứng $P$ qua $EF$ thì $L\in (O)$ . Do tính đối xứng nên $\overline{A, E, L}  và  \overline{D, F, L}$ .

Lấy $J$ là trung điểm $ST\Rightarrow JS=JT=JO$.

Mặt khác $\widehat{ESO}=\widehat{EOS}=45^\circ, \widehat{FTO}=\widehat{FOT}=45^\circ\Rightarrow ES=EO, FT=FO$

$\Rightarrow JE\perp SO, JF\perp TO\Rightarrow JE\perp JF.$. Mà$\widehat{JEF}=\widehat{JFE}=45^\circ$

$\Rightarrow JE=JF$.

Mặt khác $\widehat{ELF}= 45^\circ=\frac{1}{2} \widehat{EJF}\Rightarrow JL= JE= JF\Rightarrow L, J, O$  thẳng hàng ( vị tự ).

Mà $\widehat{UEL}=2 \widehat{BAL}=\widehat{BOL}= \frac{1}{2} \widehat{UJL}\Rightarrow U\in (J,JE)\Rightarrow JU= JL$

Tương tự $JL=JV\Rightarrow L\in (UV)$ 

Rõ ràng, ta suy ra $(UV)$ tiếp xúc $(O).\blacksquare$

Lời giải của em đoạn "Mà $\widehat{UEL}=2 \widehat{BAL}=\widehat{BOL}= \frac{1}{2} \widehat{UJL}\Rightarrow U\in (J,JE)\Rightarrow JU= JL$" chưa ổn lắm vì chưa có tam giác JUL cần sao suy ra được J là tâm.

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 06-06-2016 - 12:34

[babystudymaths]

Lời giải của em đoạn "Mà $\widehat{UEL}=2 \widehat{BAL}=\widehat{BOL}= \frac{1}{2} \widehat{UJL}\Rightarrow U\in (J,JE)\Rightarrow JU= JL$" chưa ổn lắm vì chưa có tam giác JUL cần sao suy ra được J là tâm.

Thưa thầy, đoạn đấy em làm như sau :

Tia JU cắt (J, JE) tại U' 

Khi đó $\widehat{UEL}= \frac{1}{2}\widehat{UJL}= \frac{1}{2}\widehat{U'JL}=\widehat{U'EL}$ => $U'\in BE=> U'\equiv U$

Bài viết đã được chỉnh sửa nội dung bởi babystudymaths: 06-06-2016 - 14:57

[quanghung86]

Làm thế cũng được nhưng cảm giác không chặt chẽ lắm!

[quanghung86]

Việc phát biểu lại bài toán như của Dương làm mở rộng của Bảo rất nhiều ý nghĩa, nếu xem nó là mở rộng của đường tròn mixtilinear, ta sẽ có tính chất mở rộng sau

 

Cho $P,Q$ đẳng giác trong tam giác $ABC$. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA,AB$ tại $P_{ac},P_{ab}$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA,AB$ tại $Q_{ac},Q_{ab}$. Thì $P_{ac},P_{ab},Q_{ac},Q_{ab}$ cùng thuộc một đường tròn $(O_a)$ tiếp xúc $(O)$ tại $A_a$. Tương tự có $B_b,C_c$ thì $AA_a,BB_b,CC_c$ đồng quy.

[baopbc]

Ngoài tính chất trên thì có rất nhiều tính chất thú vị khác cũng đúng! Sau đây là các phát biểu của anh Dương gửi cho em!

Cho $P,Q$ đẳng giác trong tam giác $ABC$. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA,AB$ tại $P_{ac},P_{ab}$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA,AB$ tại $Q_{ac},Q_{ab}$. Thì $P_{ac},P_{ab},Q_{ac},Q_{ab}$ cùng thuộc một đường tròn $(O_a)$ tiếp xúc $(O)$ tại $A_a$. Tương tự có $B_b,C_c$.

a) $AA_a,BB_b,CC_c$ đồng quy tại $I$.

b) Gọi $O_a,O_b,O_c$ lần lượt là tâm các đường tròn tiếp xúc với $(O)$. Chứng minh rằng $AO_a,BO_b,CO_c$ đồng quy tại $J$.

c) Chứng minh rằng $O,I,J$ thẳng hàng.

Hình vẽ

 

 

[quanghung86]

Tính chất thẳng hàng hay quá, một tính chất khác

 

c) $B_bC_c,BC,O_bO_c$ đồng quy.

[QuangDuong12011998]

Thưa thầy và các bạn, đường tròn mixtilinear có nhiều tính chất đẹp, cả mixtilinear trong lẫn ngoài.

Với cảm nhận hình học của mình, em tin có thể mở rộng được một lượng rất lớn các tính chất đẹp của đường tròn mixtilinear.

Đặc biệt là đường thẳng mà Bảo nêu trên chắc hẳn còn chứa nhiều điểm khác - tương tự đường thẳng $OI$.

Nhất định em sẽ đào sâu vấn đề này 

[quanghung86]

Cám ơn các em về các phát triển hay và ý nghĩa. Thầy cũng đang muốn tìm cái mở rộng của đẳng giác Nagel là tâm vị tự ngoài $(O),(I)$ trên mô hình này .

[TQHKTH]

Bài toán tổng quát của bạn Bảo quá hay! Mình xin trình bày cách giải của mình bên cạnh lời giải đã có của Quang Dương

 

Bài toán. Cho $\triangle ABC$ có $P, Q$ là 2 điểm đẳng giác. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA, AB$ tại $X, Y$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA, AB$ tại $Z, T$. Chứng minh rằng $X, Y, Z, T$ đồng viên trên đường tròn $\omega$ tiếp xúc $(ABC)$

Lời giải. Gọi $BP\cap (O) = K,\ BQ\cap (O) = H$ và $W$ là điểm đẳng giác của $Z$ trong $\triangle CQH$. Cộng góc đơn giản ta có cặp đồng dạng quen thuộc: $\triangle CQH \sim \triangle PCK$. Tiếp tục cộng góc có: $\angle XCP = \angle QCB = \angle ZQH = \angle WQC$. Và tương tự: $\angle XPC = \angle WCQ$. Điều đó có nghĩa là ta có 2 cấu hình đồng dạng:

$\boxed{\left(\triangle CQH \cup W\right)\sim \left(\triangle PCK \cup X\right)}$

Vậy nên $\angle ZHQ = \angle WHC = \angle XKP \Rightarrow HZ,\ KX$ cắt tại $S$ trên $(O)$. Áp dụng Pascal đảo cho $\binom{S\ B\ C}{A\ E\ K}$ có $\overline{S, E, Y}$. Tương tự $\overline{S, D, T}$. Mặt khác, dễ thấy: $DE, EK, KH, HD$ lần lượt song song với $TY, YX, XZ, ZT$ nên tồn tại phép vị tự tâm $S$:

$\mathcal{H}_S^k:\ D, E, K, H\mapsto T, Y, X, Z$

Lại do $DEKH$ nội tiếp nên đương nhiên $TYXZ$ cũng sẽ nội tiếp. Hai đường tròn ngoại tiếp 2 tứ giác này là ảnh của nhau qua $\mathcal{H}_S$ nên tiếp xúc nhau.

 

PS. Thực tế lời giải sẽ chặt chẽ hơn nếu dùng góc định hướng, tuy nhiên mình nghĩ trên diễn đàn góc thường trông dễ nhìn hơn.

Hình gửi kèm

• 

[Ngockhanh99k48]

Ngoài tính chất trên thì có rất nhiều tính chất thú vị khác cũng đúng! Sau đây là các phát biểu của anh Dương gửi cho em!

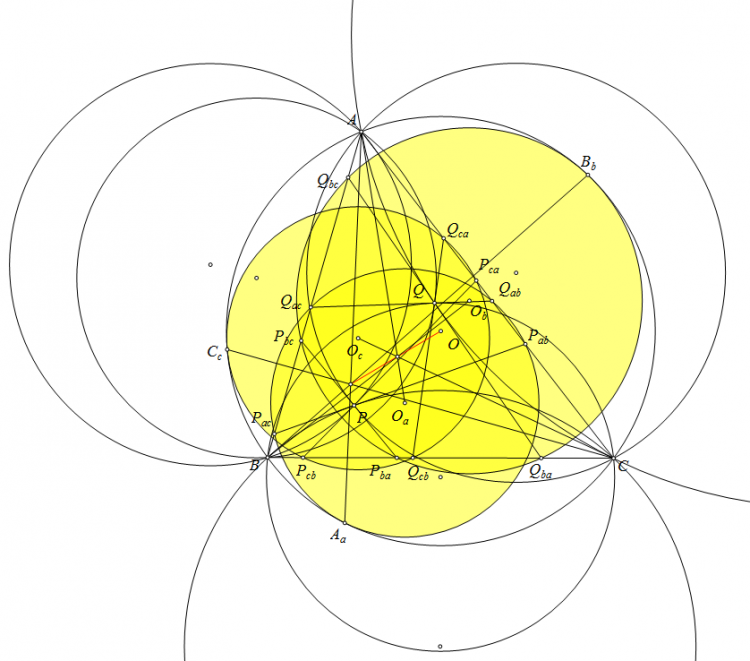
Cho $P,Q$ đẳng giác trong tam giác $ABC$. Tiếp tuyến tại $P$ của $(PBC)$ cắt $CA,AB$ tại $P_{ac},P_{ab}$. Tiếp tuyến tại $Q$ của $(QBC)$ cắt $CA,AB$ tại $Q_{ac},Q_{ab}$. Thì $P_{ac},P_{ab},Q_{ac},Q_{ab}$ cùng thuộc một đường tròn $(O_a)$ tiếp xúc $(O)$ tại $A_a$. Tương tự có $B_b,C_c$.

a) $AA_a,BB_b,CC_c$ đồng quy tại $I$.

b) Gọi $O_a,O_b,O_c$ lần lượt là tâm các đường tròn tiếp xúc với $(O)$. Chứng minh rằng $AO_a,BO_b,CO_c$ đồng quy tại $J$.

c) Chứng minh rằng $O,I,J$ thẳng hàng.

Post 193.png

Hình vẽ

Xin phép được chứng minh toàn bộ tính chất Bảo đưa ra và một tính chất thầy Hùng đăng ở post #15:

Anh Dương đã chứng minh $(O_a)$ tiếp xúc $(O)$, em xin được chứng minh theo cách khác không dùng chứng minh trùng .

Trước hết, gọi $A_a = (BPP_{ab}) \cap (ABC)$. Ta có $(PP_{ac}, PA_a) \equiv (PP_{ab}, PA_a) \equiv (BP_{ab}, BA_a) \equiv (BA, BA_a) \equiv (CA, CA_a) \equiv (CP_{ac}, CA_a)$ (mod $\pi$), do đó $C, P, P_{ac}, A_a$ đồng viên. Gọi $R = BP \cap CQ$. Ta có $(PR, PP_{ac}) \equiv (PB, PP_{ab}) \equiv (CB, CP)$ (do $PP_{ab}$ là tiếp tuyến $(PBC)$) $\equiv (CQ, CA)$ (do $P, Q$ đẳng giác) $\equiv (CR, CP_{ac})$ (mod $\pi$). Do đó $C, P, P_{ac}, A_a, R$ đồng viên. Gọi $S= BQ \cap CP$ thì tương tự ta có $S \in (BP_{ab}PA_a)$. 

Ta có $(QQ_{ac}, QS) \equiv (QQ_{ab}, QB) \equiv (CQ, CB)$ (do $QQ_{ab}$ là tiếp tuyến $(QBC)$) $\equiv (CA, CP) \equiv (CQ_{ac}, CS)$ (mod $\pi$) nên $C, Q, S, Q_{ac}$ đồng viên. Tương tự $B, Q, R, Q_{ab}$ đồng viên. Do $A_a$ là điểm Miquel của tứ giác toàn phần $PRQSBC$ nên $A_a \in (CQ_{ac}QS), A_a \in (BQ_{ab}QR)$. Ta lại có $(RQ_{ab}, RB) \equiv (QQ_{ab}, QB) \equiv (QQ_{ac}, QS) \equiv (CQ_{ac}, CS) \equiv (CP_{ac}, CP) \equiv (RP_{ac}, RP) \equiv (RP_{ac}, RB)$ (mod $\pi$). Do đó $Q_{ab}, R, P_{ac}$ thẳng hàng. Tương tự thì $P_{ab}, S, Q_{ac}$ thẳng hàng. Do đó $(P_{ac}Q_{ab}, P_{ac}Q_{ac}) \equiv (P_{ac}R, P_{ac}C)  \equiv (PR, PC) \equiv (PB, PS) \equiv (P_{ab}B, P_{ab}S) \equiv (P_{ab}Q_{ab}, P_{ab}Q_{ac})$ (mod $\pi$). Do đó $P_{ab}, P_{ac}, Q_{ab}, Q_{ac}$ đồng viên. Từ đó ta cũng có $(A_aB, A_aQ) \equiv (Q_{ab}B, Q_{ab}Q) \equiv (Q_{ab}P_{ab}, Q_{ab}Q_{ac}) \equiv (P_{ac}P_{ab}, P_{ac}Q_{ac}) \equiv (P_{ac}P, P_{ac}C) \equiv (A_aP, A_aC)$ (mod $\pi$). Do đó $A_aP, A_aQ$ đẳng giác trong góc $\widehat{BA_aC}$. 

Ta có $(A_aP_{ab}, A_aQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (A_aQ, A_aQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (SQ, SQ_{ac}) \equiv (A_aP_{ab}, A_aQ) + (SB, SP_{ab}) \equiv (A_aP_{ab}, A_aQ) + (A_aB, A_aP_{ab}) \equiv (A_aB, A_aQ) \equiv (Q_{ab}B, Q_{ab}Q) \equiv (Q_{ab}P_{ab}, Q_{ab}Q_{ac})$ (mod $\pi$). Do đó $A_a \in (P_{ab}P_{ac}Q_{ab}Q_{ac})$. Kẻ tiếp tuyến $A_ax$ của $(ABC)$. Ta có $(A_aP_{ab}, A_ax) \equiv (A_aP_{ab}, A_aB) + (A_aB, A_ax) \equiv (PP_{ab}, PB) + (CB, CA_a) \equiv (CP, CB) + (CB, CA_a) \equiv (CP, CA_a) \equiv (P_{ac}P, P_{ac}A_a) \equiv (P_{ac}P_{ab}, P_{ac}A_a)$ (mod $\pi$). Do đó $A_ax$ cũng là tiếp tuyến $(A_aP_{ab}P_{ac}Q_{ac}Q_{ab})$. Do đó $(O_a)$ tiếp xúc $(O)$ tại $A_a$. 

Bây giờ ta sẽ chứng minh bài của Bảo: 

a) Ta sẽ sử dụng bổ đề Ceva trong đường tròn: Cho $\triangle ABC$ nội tiếp $(O)$, các điểm $A', B', C'$ bất kì chạy trên $(O)$. Khi đó $AA', BB', CC'$ đồng quy $\Leftrightarrow$ $\frac{A'B}{A'C}.\frac{B'C}{B'A}.\frac{C'A}{C'B} = 1$.

Quay lại bài toán:

Ta đã có $(A_aB, A_aQ) \equiv (A_aP, A_aC)$ (mod $\pi$), mà $(QA_a, QB) \equiv (QA_a, QS) \equiv (CA_a, CS) \equiv (CA_a, CP)$ (mod $\pi$). Do đó $\triangle A_aBQ \stackrel{+}{\sim} \triangle A_aPC$. Tương tự $\triangle A_aBP \stackrel{+}{\sim} \triangle A_aQC$. Với hai cặp tam giác đồng dạng cùng hướng ta có $\frac{A_aB}{A_aC} = \frac{A_aB}{A_aP}.\frac{A_aP}{A_aC} = \frac{BQ}{PC}.\frac{BP}{QC} = \frac{BP.BQ}{CP.CQ}$.   

Khi định nghĩa tương tự với $B_b, C_c$, do sự hoán vị vòng quanh nên ta có ngay $\frac{A_aB}{A_aC}.\frac{B_bC}{B_bA}.\frac{C_cA}{C_cB}=1$. Ta có đpcm $\blacksquare$.

Trước khi chứng minh phần b) và c) của bài toán, mình sẽ chứng minh tính chất $B_bC_c, O_bO_c, BC$ đông quy.

Trước hết ta có $(A_aP_{ab}, A_aB) \equiv (PP_{ab}, PB) \equiv (CP, CB)$ (mod $\pi$). Do đó $A_aP_{ab}$ cắt $CP$ tại một điểm $C_p$ thuộc $(O)$. Tương tự định nghĩa như vậy với $A_p, B_p, A_q, B_q, C_q$.

$B_bC_c$ cắt $BC$ tại $A_1$. Dễ dàng chứng minh được $Q_{ca}Q_{cb} \parallel B_qA_q$. Do đó $(B_bC_c, B_bQ_{bc}) \equiv (B_bC_c, B_bA_q) \equiv (B_qC_c, B_qA_q) \equiv (Q_{ca}C_c, Q_{ca}Q_{cb}) \equiv (P_{cb}C_c, P_{cb}Q_{cb}) \equiv (P_{cb}C_c, P_{cb}Q_{bc})$ (mod $\pi$). Do đó $B_b, C_c, Q_{bc}, P_{cb}$ đồng viên. Tương tự $B_b, C_c, Q_{cb}, P_{bc}$ đồng viên.

Xét phép nghịch đảo cực $A_1$ biến $B_b \leftrightarrow C_c$, $P_{cb} \leftrightarrow Q_{bc}$, $P_{bc} \leftrightarrow Q_{cb}$. Do đó $(O_b) \leftrightarrow (O_c)$. Do đó $A_1, O_b, O_c$ thẳng hàng hay $B_bC_c, O_bO_c, BC$ đồng quy $\blacksquare$.

b) Định nghĩa: Cho $\triangle ABC, \triangle DEF$ có $AD, BE, CF$ đồng quy tại $M$ thì $M$ gọi là tâm phối cảnh của hai tam giác $\triangle ABC, \triangle DEF$. Và nếu $X = AB \cap DE, Y =BC \cap EF, Z =CA \cap FD$ thì $\overline{XYZ}$ gọi là trục phối cảnh của hai tam giác $\triangle ABC, \triangle DEF$.

Ta có nếu định nghĩa tương tự với $B_1, C_1$ tương tự $A_1$ thì do $\triangle O_aO_bO_c, \triangle A_aB_bC_c$ nhận $O$ là tâm phối cảnh nên $\overline{A_1B_1C_1}$ là trục phối cảnh của $\triangle A_aB_bC_c$ và $\triangle O_aO_bO_c$. Do tính chất đồng quy và chứng minh trên: $B_bC_c, O_bO_c, BC$ đồng quy, nên $\overline{A_1B_1C_1}$ là trục phối cảnh của $\triangle ABC$ và $\triangle O_aO_bO_c$. Do đó $AO_a, BO_b, CO_c$ đồng quy tại $J$.

c) Ta sử dụng bổ đề sau. Cho $\triangle ABC, \triangle MNP, \triangle XYZ$ có chung trục phối cảnh. Khi đó 3 tâm phối cảnh của $\triangle ABC, \triangle MNP , \triangle XYZ$ thẳng hàng. (Điều này dễ dàng chứng minh được nhờ Pappus, Menelaus như khi mình chứng minh định lí Desargues). 

Xét tam giác $\triangle ABC, \triangle O_aO_bO_c, \triangle A_aB_bC_c$ có chung trục phối cảnh nên 3 tâm phối cảnh $O, I, J$ thẳng hàng $\blacksquare$. 

[Ngockhanh99k48]

Một chất chất khác giống điểm Nagel mà em vừa tìm thấy như sau:

Gọi $G$ là trọng tâm $\triangle ABC$, $M$ là trung điểm $PQ$ và $I*$ là liên hợp đẳng giác của $I$ (đồng quy của $AA_a, BB_b, CC_c$) thì $\overrightarrow {GI*} = 2\overrightarrow{MG}$