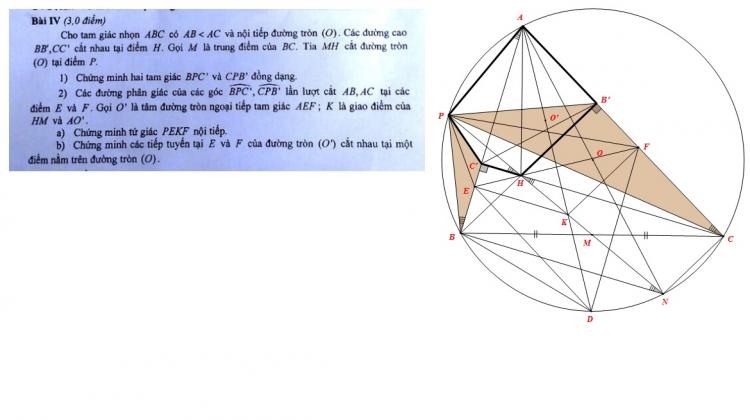
Đề tuyển sinh chuyên Hà Nội 2016-2017
#1
 Đã gửi 09-06-2016 - 17:40
Đã gửi 09-06-2016 - 17:40

#2
 Đã gửi 09-06-2016 - 18:07
Đã gửi 09-06-2016 - 18:07

Câu V:
Giả sử tồn tại $2017$ SHT được sắp xếp $1$ cách thoả mãn nếu bỏ $2$ số bất kì cạnh nhau thì $2015$ số còn lại chia được thành $2$ nhóm có tổng bằng nhau. Gọi $2017$ số được sắp xếp thoả mãn là $2017$ số có tính chất $P$
Vì có $2017$ SHT có tính chất $P$ nên nếu nhân mẫu của các SHT đó lên thì được $2017$ STN có tính chất $P$. Gọi $2017$ số đó lần lượt xếp theo chiều kim đồng hồ là $a_{1};a_{2};...;a_{2017}$. Giả sử trong $2017$ số đó có 1 số chẵn, 1 số lẻ thì vì $2017$ là số lẻ nên lúc đó trên vòng tròn tồn tại $2$ số liền kề cùng tính chẵn lẻ và $2$ số liền kề không cùng tính chẵn lẻ. Vì vậy có thể bỏ 1 trong 2 cặp số đó để tổng $2015$ số còn lại lẻ, lúc đó thì không thể có cách chia $2015$ số còn lại thoả mãn đề bài. Giả sử tất cả các số trên vòng tròn cùng tính chẵn lẻ, $2017$ số đó không thể cùng lẻ vì cho dù bỏ đi $2$ số nào thì tổng các số còn lại đều lẻ nên không thể chia được. Vậy tất cả các số trên vòng tròn đều chẵn. Đặt $a_{i}=2b_{i}$ với $i$ chạy từ $1$ đến $2017$. Vì $2017$ số $a_{1};a_{2};...a_{2017}$ có tính chất $P$ nên $b_{1};b_{2};...b_{2017}$ cũng có tính chất $P$. Lập luận tương tự $b_{1};b_{2};...b_{2017}$ đều chẵn. Tiếp tục đặt $b_{i}=2c_{i}$ và lặp lại vô hạn bước như vậy, ta có $a_{1}=a_{2}=...=a_{2017}=0$ (vô lí vì các số hữu tỉ ban đầu dương)
Suy ra dpcm
Bài viết đã được chỉnh sửa nội dung bởi JUV: 09-06-2016 - 18:07
- lehongquan99 và the unknown thích
#3
 Đã gửi 09-06-2016 - 19:07
Đã gửi 09-06-2016 - 19:07

#4
 Đã gửi 09-06-2016 - 19:43
Đã gửi 09-06-2016 - 19:43

Câu III.1:
Ta có: $a^2+b^2+c^2\geq \frac{(a+b+c)^2}{3} \Rightarrow a+b+c\leq 3$. Vậy ta có $3(ab+bc+ca)\leq (a+b+c)^2\leq 3(a+b+c)\Rightarrow ab+bc+ca\leq a+b+c$
Ta có: $\sum \frac{2a^2}{a+b^2}=\sum (2a-\frac{2ab^2}{a+b^2})\geq \sum (2a-\frac{2ab^2}{2b\sqrt{a}})=2(a+b+c)-(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})$.
Mặt khác theo bất đẳng thức Bunyakovsky ta có: $(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})^2=(\sqrt{a}\sqrt{ac}+\sqrt{c}\sqrt{bc}+\sqrt{b}\sqrt{ab})^2\leq (a+b+c)(ab+bc+ca)\leq (a+b+c)^2\Rightarrow (a\sqrt{c}+c\sqrt{b}+b\sqrt{a})\leq a+b+c$
Do đó $\sum \frac{2a^2}{a+b^2}\geq 2(a+b+c)-(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})\geq 2(a+b+c)-(a+b+c)=a+b+c$.
Vậy bài toán được chứng minh. Đẳng thức xảy ra khi và chỉ khi $a=b=c=1$.
Bài viết đã được chỉnh sửa nội dung bởi the unknown: 09-06-2016 - 19:46
- CaptainCuong và Baoriven thích
$\texttt{If you don't know where you are going, any road will get you there}$
#5
 Đã gửi 09-06-2016 - 19:44
Đã gửi 09-06-2016 - 19:44

Mình xin chém câu bất (ms nghĩ ra @@)
Ta có: VT = $\frac{1}{1+\frac{b^{2}}{a}}+\frac{1}{1+\frac{c^{2}}{b}}+\frac{1}{1+\frac{a^{2}}{c}}$
Mà $(1+\frac{b^{2}}{a})(1+a)\geq (1+b)^{2}$ => VT $\leq \frac{1+a}{(1+b)^{2}}+\frac{1+b}{(1+c)^{2}}+\frac{1+c}{(1+a)^{2}}$
$=\sum \frac{1+a}{(a+2b+c)^{2}}\leq \frac{1}{4}\sum \frac{1+a}{(a+b)(b+c)}=\frac{1}{4}\frac{\sum (1+a)(1-b)}{\prod(1-a)}=\frac{1}{4}*\frac{3-(ab+bc+ca)}{ab+bc+ca-abc}$
Ta chứng minh $\frac{3-(ab+bc+ca)}{ab+bc+ca-abc}\leq \frac{1}{a}+\frac{1}{b}+\frac{1}{c}$
$<=>(ab+bc+ca)^{2}\geq 3abc$ (đúng do a+b+c = 1)
Dấu "=" xảy ra khi a = b = c = $\frac{1}{3}$.
- audreyrobertcollins, hoakute và quankun134 thích
#6
 Đã gửi 09-06-2016 - 20:11
Đã gửi 09-06-2016 - 20:11

Kí hiệu $101$ số nguyên dương xếp thứ tự trên vòng tròn là $a_1,a_2,a_3,...,a_{100},a_{101}$. Khi đó với số nguyên dương $i$, $1\leq i\leq 101$. Ta đặt: $S_i=a_1+a_2+a_3+...+a_i$.
Với cách đặt như vậy, để ý rằng theo Dirichlet thì trong $101$ số $S_1;S_2;S_3;...;S_{101}$ tồn tại hai số $S_i;S_j$ ( $1\leq i<j\leq 101$, $i,j$ nguyên dương ) thì ta có $S_i\equiv S_j(mod 100)$. Tức là $100\mid S_j-S_i=a_i+a_{i+1}+...+a_j$.
Nếu $a_i+a_{i+1}+...+a_j=100$ thì ta có điều phải chứng minh.
Nếu $a_i+a_{i+1}+...+a_j=200$ thì khi đó tổng các số của một dãy liên tiếp từ $a_{j+1}$ tới $a_{i-1}$ (với quy ước rằng $a_0=a_{101}$, $a_1=a_{102}$ ) sẽ bằng $100$. Vậy ta cũng có điều phải chứng minh.
Vậy bài toán được chứng minh.
- audreyrobertcollins và hoakute thích
$\texttt{If you don't know where you are going, any road will get you there}$
#7
 Đã gửi 09-06-2016 - 21:38
Đã gửi 09-06-2016 - 21:38

2) Từ giả thiết suy ra $y=2t$ ($t$ là số tự nhiên)
$PT<=>2^x.x^2=(6t)^2+12t+16$
Dễ thấy với $x\leqslant 3$ thì $x=2$ thoả mãn
Xét $x\geqslant 4$ suy ra $VT\vdots 16$
mà $VP\equiv 4$ $(mod 6)$ nên $PT$ vô nghiệm
Suy ra $x=2$ và $y=0$
#8
 Đã gửi 10-06-2016 - 09:56
Đã gửi 10-06-2016 - 09:56

#9
 Đã gửi 10-06-2016 - 10:12
Đã gửi 10-06-2016 - 10:12

Câu III.1:
Ta có: $a^2+b^2+c^2\geq \frac{(a+b+c)^2}{3} \Rightarrow a+b+c\leq 3$. Vậy ta có $3(ab+bc+ca)\leq (a+b+c)^2\leq 3(a+b+c)\Rightarrow ab+bc+ca\leq a+b+c$
Ta có: $\sum \frac{2a^2}{a+b^2}=\sum (2a-\frac{2ab^2}{a+b^2})\geq \sum (2a-\frac{2ab^2}{2b\sqrt{a}})=2(a+b+c)-(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})$.
Mặt khác theo bất đẳng thức Bunyakovsky ta có: $(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})^2=(\sqrt{a}\sqrt{ac}+\sqrt{c}\sqrt{bc}+\sqrt{b}\sqrt{ab})^2\leq (a+b+c)(ab+bc+ca)\leq (a+b+c)^2\Rightarrow (a\sqrt{c}+c\sqrt{b}+b\sqrt{a})\leq a+b+c$
Do đó $\sum \frac{2a^2}{a+b^2}\geq 2(a+b+c)-(a\sqrt{c}+c\sqrt{b}+b\sqrt{a})\geq 2(a+b+c)-(a+b+c)=a+b+c$.
Vậy bài toán được chứng minh. Đẳng thức xảy ra khi và chỉ khi $a=b=c=1$.
Cách khác :
Áp dụng bất đẳng thức Cauchy-Swarchz :
$VT \ge \frac{(\sum 2a^2)^2}{\sum 2a^3+\sum 2a^2b^2} \ge \frac{36}{\sum (a^4+a^2)+\sum 2a^2b^2}=\frac{36}{(\sum a^2)^2+\sum a^2}=3 \ge a+b+c$
Vì $\sqrt{9}=\sqrt{(\sum a^2).3} \ge \sum a$
#10
 Đã gửi 10-06-2016 - 16:35
Đã gửi 10-06-2016 - 16:35

Câu 1:
a, Ta có:
Pt$\Leftrightarrow (x^2-x)^2+(x^2-x)-\sqrt{2(x^2-x)}=0$
Đặt $\sqrt{x^2-x}= y (y\geq 0)$ thì ta có:
$y^4+y^2-\sqrt{2}y$=0
$\Leftrightarrow y(y^3+y-\sqrt{2})=0$
$\Leftrightarrow y(y-\sqrt{2})(y^2+\sqrt{2}y+1)= 0$
$\begin{matrix} y=o\\ y=\sqrt{2}\end{matrix}$
Đến đây thì đơn giản rồi
Nothing in your eyes
#11
 Đã gửi 10-06-2016 - 16:42
Đã gửi 10-06-2016 - 16:42

Bài 1b:
Ta có:
HPT$\Leftrightarrow \left\{\begin{matrix} (x-2)^2=-2y+4\\ (2x-y^2)^2-2y+4=0\end{matrix}\right.$
$\Rightarrow (2x-y^2)^2+(x-2)^2=0$
Đến đây tìm nguyệm đơn giản rồi
Nothing in your eyes
#12
 Đã gửi 10-06-2016 - 23:32
Đã gửi 10-06-2016 - 23:32

#13
 Đã gửi 23-06-2016 - 16:40
Đã gửi 23-06-2016 - 16:40

mọi người giúp em bài hình của chuyên tin được ko ạ?
#14
 Đã gửi 13-08-2016 - 16:30
Đã gửi 13-08-2016 - 16:30

Đã có đáp án ở đây!
Anh ơi! Gợi ý giúp em ý 2b của bài hình với ạ.
#15
 Đã gửi 17-08-2016 - 14:39
Đã gửi 17-08-2016 - 14:39

Anh ơi! Gợi ý giúp em ý 2b của bài hình với ạ.
Gợi ý: Theo hình vẽ của em nhé!
Sử dụng định lý đường phân giác lập tỉ số ta dễ dàng chứng minh được $HE$, $HF$ lần lượt là phân giác góc $\angle C'HB$, $\angle B'HC$ => tam giác AEF cân tại A. => $AD$ là trung trực của $EF$
Kéo dài $CC'$ cắt (O) tại $C_1$. Ta dễ có $HC'=C'C_1$ => $E$ là giao điểm của ba đường phân giác của tam giác $C_1BH$. Mà $C_1D$ là phân giác của góc $BC_1H$ => $C_1, E, D$ thẳng hàng.
Ta có $EK//C_1H$ => $\angle DEK=\angle DC_1H=\frac{1}{2}\angle BAC=\angle EAK$ => $DE$ là tiếp tuyến của (O') tại E.
Tương tự đối với $DF$ => đpcm.
$Maths$, $Smart Home$ and $Penjing$
123 Phạm Thị Ngư
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh