Chủ đề này có 17 trả lời

[Dinh Xuan Hung]

              SỞ GIÁO DỤC VÀ ĐÀO TẠO                                    ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN

                           NINH BÌNH                                                                       NĂM HỌC 2016-2017

               $\boxed{\textrm{ĐỀ THI CHÍNH THỨC}}$                             Thời gian làm bài 150 phút (không kể thời gian giao đề)

 

                                                                                                                                                                             

 

                                                                                                            Đề thi gồm 05 câu trong 01 trang

 

Câu 1 (1,5 điểm).

 

Cho biểu thức:           $P=\frac{2x-11\sqrt{x}+15}{x-4\sqrt{x}+3}+\frac{3\sqrt{x}}{\sqrt{x}-1}-\frac{\sqrt{x}-1}{\sqrt{x}-3}$

 

1.Rút gon biểu thức $P$

 

2.Tính giá trị của $P$ khi $x=11+6\sqrt{2}$

 

Câu 2 (1,5 điểm).

 

Cho parabol $(P):y=x^2$ và đường thẳng $(d):y=2mx-2m+3$ (với $m$ là tham số) .Tìm tất cả các giá trị của $m$ để đường thẳng $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1;x_2$ sao cho $2(x_1^2+x_2^2)+3(x_1+x_2)=18$

 

Câu 3 (2,0 điểm).

 

1.Giải phương trình : $\sqrt{x^2+12}-\sqrt{x^2+5}=3x-5$

 

2.Giải hệ phương trình:$\left\{\begin{matrix} 3x^2+2y+4=2z(x+3) & & & \\ 3y^2+2z+4=2x(y+3) & & & \\ 3z^2+2x+4=2y(z+3) & & & \end{matrix}\right.$

 

Câu 4 (3,5 điểm).

 

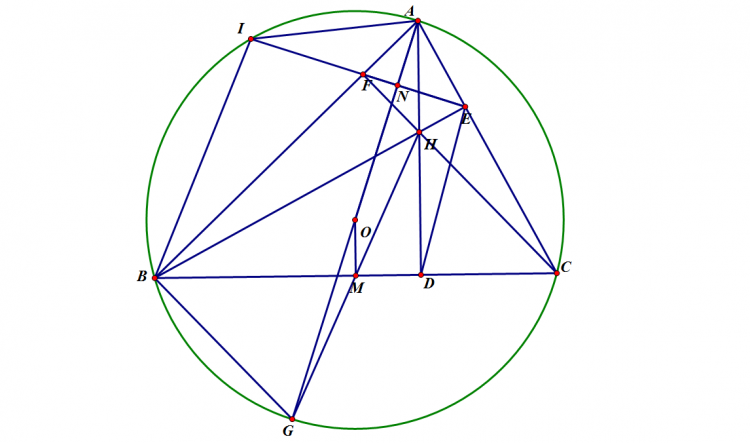
Cho đường tròn $(O)$ bán kính $R$ , dây $BC$ cố định khác đường kính , $A$ là một điểm động trên cung lớn $BC$ sao cho tam giác $ABC$ nhọn . Các đường cao $BE,CF$ của tam giác $ABC$ cắt nhau tại $H$ 

 

1.Chứng minh tứ giác $BCEF$ là tứ giác nội tiếp và $AO$ vuông góc với $EF$

 

2.Tia $EF$ cắt đường tròn $(O)$ tại $I$ , tia $AO$ cắt đường tròn $(O)$ tại $G$ . Gọi $M$ là trung điểm của $BC$ , $D$ là giao điểm của hai đường thẳng $AH$ và $BC$

Chứng minh : $AI^2=2AD.OM$

 

3.Trong trường hợp tam giác $ABC$ cân tại $A$ . Gọi $x$ là khoảng cách từ $(O)$ đến $BC$. Tìm $x$ để chu vi tam giác $ABC$ lớn nhất

 

Câu 5 (1,5 điểm).

 

1.Cho $a,b,c$ là các số thực dương thỏa mãn : $abc=1$ . Chứng minh rằng:

 

$$\frac{1}{ab+a+2}+\frac{1}{bc+b+2}+\frac{1}{ca+c+2}\leq \frac{3}{4}$$

 

2.Tìm tất cả các cặp số nguyên $(x;y)$ thỏa mãn: $1+x+x^2+x^3+x^4=y^2$

 

                                                                                HẾT                                                                                                       

Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 11-06-2016 - 21:01

[O0NgocDuy0O]

Câu 3:

1) ĐK: $x\geq \frac{5}{3}.$

$PT\Leftrightarrow (\sqrt{x^{2}+12}-4)-(\sqrt{x^{2}+5}-3)=3(x-2)\Leftrightarrow \frac{x^{2}-4}{\sqrt{x^{2}+12}+4}-\frac{x^{2}-4}{\sqrt{x^{2}+5}+3}=3(x-2)$

$\Leftrightarrow \begin{bmatrix} x=2\\ \frac{1}{\sqrt{x^{2}+12}+4}-\frac{1}{\sqrt{x^{2}+5}+3}-3=0 \end{bmatrix}$

Bài viết đã được chỉnh sửa nội dung bởi O0NgocDuy0O: 11-06-2016 - 21:15

[Thislife]

      Câu 5 (1,5 điểm).

 

1.Cho $a,b,c$ là các số thực dương thỏa mãn : $abc=1$ . Chứng minh rằng:

 

$$\frac{1}{ab+a+2}+\frac{1}{bc+b+2}+\frac{1}{ca+c+2}\leq \frac{3}{4}$$

                                            

Đặt $(a,b,c) = (\frac{x}{y}, \frac{y}{z}, \frac{z}{x} )$ ,ta được :

$VT=\sum \frac{yz}{xy+xz+2yz} \leq \frac{1}{4} \sum (\frac{yz}{xy+yz} +\frac{yz}{yz+xz} )= \frac{1}{4} \sum (\frac{z}{x+z} +\frac{y}{x+y} )= \frac{3}{4}$

Bài viết đã được chỉnh sửa nội dung bởi Thislife: 11-06-2016 - 21:24

[O0NgocDuy0O]

Câu 5: 

2)$(2y)^{2}=4x^{4}+4x^{3}+4x^{2}+4x+4\Leftrightarrow (2x^{2}+x)^{2}<(2y)^{2}\leq (2x^{2}+x+2)\Rightarrow \begin{bmatrix} (2y)^{2}=2x^{2}+x+1\\ (2y)^{2}=2x^{2}+x+2 \end{bmatrix}.$

Câu 3:

2) Cộng vế với vế:

$(x-y)^2+(y-z)^2+(z-x)^2+(x-2)^2+(y-2)^2+(z-2)^2=0.$

$\Rightarrow x=y=z=2$

Bài viết đã được chỉnh sửa nội dung bởi O0NgocDuy0O: 11-06-2016 - 21:38

[Baoriven]

Câu 3b)

Cộng theo vế 3 phương trình ta được: 

$(x-y)^2+(y-z)^2+(z-x)^2+(x-2)^2+(y-2)^2+(z-2)^2=0$

Vậy phương trình có nghiệm x=y=z=2

[anhminhnam]

Câu 5 Ta có phương trình tương đương

$(2y)^2=(2x^2+x)^2+2x^2+(x+2)^2 =>(2y)^2>(2x^2+x)^2 \Rightarrow (2y)^2\geq (2x^2+x+1)^2$ (xét x nguyên)

$\Leftrightarrow 4(x^4+x^3+x^2+x+1)\geq (2x^2+x+1)^2$ (chỗ này đánh giá được do 2x^2+x\geq 0 với mọi x nguyên)

$\Leftrightarrow -1\leq x\leq 3$ 

Từ đó thử và thu được các bộ thoả (-1;1) (-1;-1) (0;1) (0;-1) (3;11) (3;-11)

Bài viết đã được chỉnh sửa nội dung bởi anhminhnam: 12-06-2016 - 08:08

[dtngoc]

Đặt $(a,b,c) = (\frac{x}{y}, \frac{y}{z}, \frac{z}{x} )$ ,ta được :

$VT=\sum \frac{yz}{xy+xz+2yz} \leq \frac{1}{4} \sum (\frac{yz}{xy+yz} +\frac{yz}{yz+xz} )= \frac{1}{4} \sum (\frac{z}{x+z} +\frac{y}{x+y} )= \frac{3}{4}$

 Ta có: $\frac{4}{{ab + a + 2}} = \frac{4}{{ab + 1 + a + 1}} = \frac{4}{{ab + abc + a + 1}} = \frac{4}{{ab\left( {c + 1} \right) + \left( {a + 1} \right)}}$

Từ đó: $\frac{4}{{ab + a + 2}} \le \frac{1}{{ab\left( {c + 1} \right)}} + \frac{1}{{a + 1}} = \frac{{abc}}{{ab\left( {c + 1} \right)}} + \frac{1}{{a + 1}} = \frac{c}{{c + 1}} + \frac{1}{{a + 1}}$

Tương tự: $\frac{4}{{bc + b + 2}} \le \frac{a}{{a + 1}} + \frac{1}{{b + 1}};\frac{4}{{ca + c + 2}} \le \frac{b}{{b + 1}} + \frac{1}{{c + 1}}$

Từ đó: $\frac{4}{{ab + a + 2}} + \frac{4}{{bc + b + 2}} + \frac{4}{{ca + c + 2}} \le \frac{{a + 1}}{{a + 1}} + \frac{{b + 1}}{{b + 1}} + \frac{{c + 1}}{{c + 1}} = 3$

$ \Rightarrow \frac{1}{{ab + a + 2}} + \frac{1}{{bc + b + 2}} + \frac{1}{{ca + c + 2}} \le \frac{3}{4}$

Dấu bằng xảy ra khi $a = b = c = 1$.

[ssYugiohss]

Ae cho mình đáp án của bài hình đi mình vừa thi đề này xong

[Oo Nguyen Hoang Nguyen oO]

Bài hình:

a) $\widehat{BFC}=\widehat{BEC}=90^{\circ}\Rightarrow$ $BCEF$ là tứ giác nội tiếp

Gọi $N$ là giao điểm của $AO$ và $EF$, ta có: $\widehat{GAC}+\widehat{AEF}=\widehat{GBC}+\widehat{ABC}=\widehat{ABG}$ (do $BCEF$ là tứ giác nội tiếp)

Mà: tam giác $ABG$ nội tiếp đường tròn đường kính $AG$ nên tam giác $ABG$ vuông ở $B$, suy ra $\widehat{ABG}=90^{\circ}$, suy ra $\widehat{GAC}+\widehat{AEF}=90^{\circ}$

Vậy $AO$ vuông góc $EF$

b) Đầu tiên gọi $G'$ là điểm đối xứng của $H$ qua $M$, suy ra $BHCG'$ là hình bình hành nên góc $BG'C$ bằng góc $BHC$ và bằng $180^{\circ}-\widehat{BAC}$, suy ra $A,B,G',C$ cùng thuộc một đường tròn nên $G$ trùng $G'$

Đến đây ta có: $OM$ là đường trung bình của tam giác $AGH$ nên $2OM.AD=AH.AD$

Dễ CM: $AH.AD=AF.AB$ do cặp tam giác $AFH$ và $ADB$ đồng dạng với nhau (g.g)

Bài toán chuyển về thành chứng minh $AI^2=AF.AB$

Có: $BCEF$ là tứ giác nội tiếp nên $\widehat{AFI}=\widehat{BFE}=180^{\circ}-\widehat{ACB}=\widehat{AIB}$ nên 2 tam giác $AFI$ và $AIB$ đồng dạng (g.g)

Suy ra: $AI^2=AF.AB$

Vậy ta có điều phải chứng minh

c) tam giác $ABC$ cân ở $A$ nên dễ dàng CM $A$ là điểm chính giữa cung lớn $BC$, khi này để $P$ lớn nhất thì mình dự đoán $x=0$ chứ chả biết làm

Hình gửi kèm

• 

[kunsomeone]

Câu 3:

1) ĐK: $x\geq \frac{5}{3}.$

$PT\Leftrightarrow (\sqrt{x^{2}+12}-4)-(\sqrt{x^{2}+5}-3)=3(x-2)\Leftrightarrow \frac{x^{2}-4}{\sqrt{x^{2}+12}+4}-\frac{x^{2}-4}{\sqrt{x^{2}+5}+3}=3(x-2)$

$\Leftrightarrow \begin{bmatrix} x=2\\ \frac{1}{\sqrt{x^{2}+12}+4}-\frac{1}{\sqrt{x^{2}+5}+3}-3=0 \end{bmatrix}$

TH thứ $2$ làm thế nào tiếp hở bạn?

[kunsomeone]

Đặt $(a,b,c) = (\frac{x}{y}, \frac{y}{z}, \frac{z}{x} )$ ,ta được :

$VT=\sum \frac{yz}{xy+xz+2yz} \leq \frac{1}{4} \sum (\frac{yz}{xy+yz} +\frac{yz}{yz+xz} )= \frac{1}{4} \sum (\frac{z}{x+z} +\frac{y}{x+y} )= \frac{3}{4}$

Cái này là gì bạn?

[O0NgocDuy0O]

TH thứ $2$ làm thế nào tiếp hở bạn?

$\frac{1}{\sqrt{x^{2}+12}+4}=\frac{1}{\sqrt{x^{2}+5}+3}+3\geq 3$

Mà $\frac{1}{\sqrt{x^{2}+12}+4}\leq \frac{1}{\sqrt{12}+4}< 3$

Vậy $TH2$ không xảy ra.

Phương trình có nghiệm duy nhất $x=2$.

[O0NgocDuy0O]

Cái này là gì bạn?

Tức là thay $a$ bởi $\frac{x}{y}$, .....

[nntien]

 

Bài hình:

a) $\widehat{BFC}=\widehat{BEC}=90^{\circ}\Rightarrow$ $BCEF$ là tứ giác nội tiếp

Gọi $N$ là giao điểm của $AO$ và $EF$, ta có: $\widehat{GAC}+\widehat{AEF}=\widehat{GBC}+\widehat{ABC}=\widehat{ABG}$ (do $BCEF$ là tứ giác nội tiếp)

Mà: tam giác $ABG$ nội tiếp đường tròn đường kính $AG$ nên tam giác $ABG$ vuông ở $B$, suy ra $\widehat{ABG}=90^{\circ}$, suy ra $\widehat{GAC}+\widehat{AEF}=90^{\circ}$

Vậy $AO$ vuông góc $EF$

b) Đầu tiên gọi $G'$ là điểm đối xứng của $H$ qua $M$, suy ra $BHCG'$ là hình bình hành nên góc $BG'C$ bằng góc $BHC$ và bằng $180^{\circ}-\widehat{BAC}$, suy ra $A,B,G',C$ cùng thuộc một đường tròn nên $G$ trùng $G'$

Đến đây ta có: $OM$ là đường trung bình của tam giác $AGH$ nên $2OM.AD=AH.AD$

Dễ CM: $AH.AD=AF.AB$ do cặp tam giác $AFH$ và $ADB$ đồng dạng với nhau (g.g)

Bài toán chuyển về thành chứng minh $AI^2=AF.AB$

Có: $BCEF$ là tứ giác nội tiếp nên $\widehat{AFI}=\widehat{BFE}=180^{\circ}-\widehat{ACB}=\widehat{AIB}$ nên 2 tam giác $AFI$ và $AIB$ đồng dạng (g.g)

Suy ra: $AI^2=AF.AB$

Vậy ta có điều phải chứng minh

c) tam giác $ABC$ cân ở $A$ nên dễ dàng CM $A$ là điểm chính giữa cung lớn $BC$, khi này để $P$ lớn nhất thì mình dự đoán $x=0$ chứ chả biết làm

 

c. tam giác ABC là tam giác đều khi đó $x=\frac{R}{2}$ (dạng này nằm trong quyển hình học cực trị của Thầy Vũ Hữu Bình)

[Nam Doc]

c. tam giác ABC là tam giác đều khi đó $x=\frac{R}{2}$ (dạng này nằm trong quyển hình học cực trị của Thầy Vũ Hữu Bình)

bạn làm cụ thể ra giúp mình với

[VoHuynh]

hình câu c / gs max khi tam giác ABC là tam giác tù , khi đó tồn tại 1 cạnh B'C' đối xứng với BC qua O nội tiếp đường tròn
đường cao ha từ A xuống BC < đường cao hạ từ A xuống B'C'
=> SABC < S AB'C' ( vô lý với điều giả sử )
Do đó S đạt max khi ABC là tam giác nhọn

khi tam giác ABC nhọn . 
Kẻ đường cao AH của tam giác ABC . 
ta có S ABC = 1/2 BC . AH = 1/2 . căn ( R^2 - x^2 ) . ( R+x) = 1/(2 căn 3) . (3R^2 -3x^2) . (R+x) =< [1/(2 căn 3)]  ( 3R^2 -3x^2 + R^2 +2xR +x^2)/2
=[ 1/(4 căn 3) ]    (   4R^2 + 2xR - 2x^2 ) = 1/(4 căn 3)    . ( -2(x^2 -xR +1/4  R^2) +1/2R^2 +4R^2) =< 1/(4 căn 3) . (1/2 R^2 + 4R^2) ( không đổi )
dấu = khi x = R/2
 

Bài viết đã được chỉnh sửa nội dung bởi VoHuynh: 21-05-2017 - 14:39

[Haduyduc]

Nói rõ ra đi

[Haduyduc]

Nói rõ ra đi