SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2016-2017
MÔN THI: TOÁN CHUYÊN
Ngày thi: 12 tháng 6 năm 2016
Thời gian làm bài: 150 phút
ĐỀ CHÍNH THỨC
Câu 1:
a) Cho 2 số thực $a,b$ sao cho $|a|\neq |b|$ và $ab\neq 0$ thỏa mãn điều kiện:
$\frac{a-b}{a^2+ab}+\frac{a+b}{a^2-ab}=\frac{3a-b}{a^2-b^2}$
Tính giá trì của biểu thức: $P=\frac{a^3+2a^2b+3b^3}{2a^3+ab^2+b^3}$
b) Cho $m,n$ là số nguyên dương sao cho $5n+m\mid 5m+n$.Chứng minh rằng $n\mid m$
Câu 2:
a) Giải phương trình: $x^2-6x+4+2\sqrt{2x-1}=0$
b) Giải hệ phương trình: $\left\{\begin{matrix}x^3-y^3=9(x+y)\\ x^2-y^2=3 \end{matrix}\right.$
Câu 3:
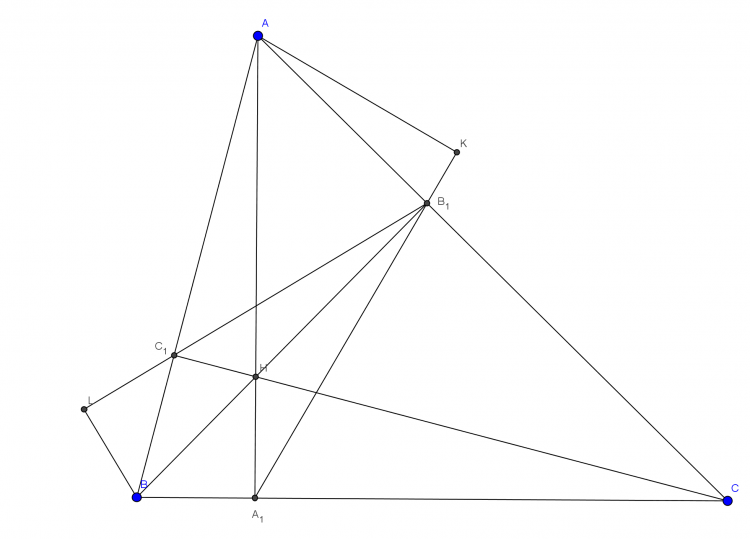
Cho tam giác $ABC$ nhọn có các đường cao $AA_1,BB_1,CC_1$.Gọi $K$ là hình chiếu của $A$ lên $A_1B_1;$ $L$ là hình chiếu của $B$ lên $B_1C_1$.Chứng minh rằng $A_1K=B_1L$
Câu 4:
Cho $x,y>0$.Chứng minh rằng: $\frac{x\sqrt{y}+y\sqrt{x}}{x+y}-\frac{x+y}{2}\leqslant \frac{1}{4}$
Câu 5:
Cho tứ giác nội tiếp $ABCD$ có $AC$ cắt $BD$ tại $E$. Tia $AD$ cắt tia $BC$ tại $F$.Dựng hình bình hành $AEBG$
a) Chứng minh: $FD.FG=FB.FE$
b) Gọi $H$ là điểm đối xứng của $E$ qua $AD.$ Chứng minh $4$ điểm $F,H,A,G$ cùng thuộc một đường tròn
Câu 6:
Nam cắt một tờ giấy ra làm $4$ miếng hoặc $8$ miếng rồi lấy một số miếng nhỏ đó cắt ra làm $4$ hoặc $8$ miếng nhỏ hơn và Nam cứ tiếp tục thực hiện việc cắt như thế nhiều lần. Hỏi Nam có thể cắt được 2016 miếng lớn,nhỏ hay không?Vì sao?