Chủ đề này có 3 trả lời

[baopbc]

Như vậy thầy Hùng đã đưa ra lời giải bài cũ tại tuần 1 tháng 9 và kèm theo đó là bài toán mới, xin trích dẫn lại bài toán mới.

 

Cho tứ giác $ABCD$ nội tiếp trong đường tròn $(O). BC$ cắt trung trực $BD$ tại $P.AP$ cắt $(O)$ tại $Q$ khác $A. CD$ cắt $OP$ tại $R$. Trên $BR$ lấy $S$ sao cho $AS\parallel BP$. Lấy $T$ thuộc $AC$ sao cho $ST\parallel BQ$. Chứng minh rằng $TA=TB$.

Hình vẽ bài toán

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 04-09-2016 - 18:33

[baopbc]

Hình vẽ bài toán

$\textbf{Lời giải.}$ Gọi $N$ là giao điểm của $BQ$ với $AC.M$ là giao điểm của $BS$ với $(O)$. Do $R$ là giao điểm của $OP$ với $CD$ nên $D,M,P$ thẳng hàng.

Xét cực đối cực với đường tròn $O$. Do $N,R$ lần lượt liên hợp với $P$ nên $NR$ là đường đối cực của $P$ đối với $(O)$. Do đó mà $NR\parallel CM\parallel BD$.

Đường thẳng qua $C\parallel AB$ cắt $BM$ tại $H$. Do $NR\parallel BD$ nên $\angle NRC=\frac{1}{2}\angle BRC$ suy ra $\angle HRN=\angle NRC=\angle NCH$ nên tứ giác $NCRH$ nội tiếp.

Từ đó $\angle NHC=\angle NCH$ nên $NH=NC$. Mặt khác do $\triangle BHC\sim \triangle SBA$ (góc - góc), $BC\parallel AS, ST\parallel BN$ nên $TA=TB$. $\blacksquare$

 

Bài viết đã được chỉnh sửa nội dung bởi baopbc: 04-09-2016 - 19:55

[quanghung86]

Cám ơn Bảo về lời giải hay, bài toán này thầy cũng dựa trên cực đối cực ra đề nhưng em làm gọn hơn thầy. Trên mô hình bài toán này có nhiều ứng dụng thú vị. Chúng ra hãy cũng thảo luận. Ví dụ ứng dụng khi đối xứng hóa bài này ta thu được bài toán như sau

 

Cho tứ giác $ABCD$ nội tiếp trong đường tròn $(O).$ $BC,AD$ lần lượt cắt trung trực $BD,AC$ tại $P,Q$. $AP,BQ$ cắt $(O)$ tại $M,N$ khác $A,B.$ $CD$ cắt $OP,OQ$ lần lượt tại $K,L$. Trên $BK,AL$ lấy $S,T$ sao cho $AS\parallel BC,BT\parallel AD$. Lấy $U,V$ lần lượt thuộc $AC,BD$ sao cho $SU\parallel BM,TV\parallel AN$. Chứng minh rằng $UV\perp AB$.

[viet nam in my heart]

Rảnh rỗi làm thử bài tuần này không biết có giống cách của Bảo không. Nếu giống thì coi như là gõ lại 

Từ giả thiết dễ thấy $DOPC$ nội tiếp nên $OP.OR=OR^2-RP.RO=OR^2-RC.RD=r^2$ trong đó $r$ là bán kính của $(O)$

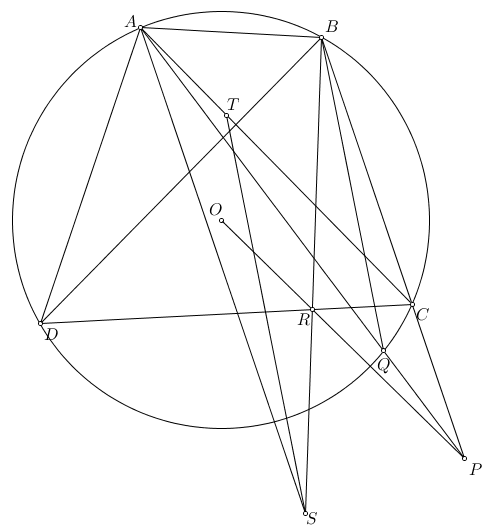
Do đó theo một bổ đề quen thuộc ta quy bài toán về: Cho tam giác $ABC$ nội tiếp $(O)$. $P$ trên $BC$. $AP$ cắt $BC$ tại $Q$. $BQ,CQ$ cắt $AC,AB$ tại $N,M$. $OP$ cắt $MN$ tại $R$. $S$ nằm trên $BR$ sao cho $AS \parallel BC$. $T$ nằm trên $AC$ sao cho $ST \parallel BQ$. Chứng minh rằng $TA=TB$

Dễ thấy $R$ là điểm $Miquel$ của tứ giác toàn phần $ABCNM$

Gọi $T'$ là điểm trên $AC$ sao cho $T'A=T'B$. Gọi $S'$ là điểm nằm trên $BR$ sao cho $T'S'\parallel BN$. Cần chứng minh $AS' \parallel BC$

Thật vậy từ trên dễ thấy $B,O,C,R$ cùng nằm trên một đường tròn. Mặt khác do $T'A=T'B$ nên $B,O,T',C$ cùng thuộc một đường tròn. Do đó $5$ điểm $B,O,C,T',R$ cùng nằm trên một đường tròn

Do $R$ là điểm $Miquel$ nên $ABRN,MBQR$ nội tiếp 

Do đó: $\widehat{BS'T'}=\widehat{RBN}=\widehat{RAN}$ nên $AS'RT'$ nội tiếp  

Suy ra $\widehat{AS'R}=\widehat{RT'C}=\widehat{RBC}$ nên $AS' \parallel BC$ 

Do đó ta có điều phải chứng minh $\blacksquare$