ĐỀ THI CHỌN ĐỘI TUYỂN QUỐC GIA THPT CHUYÊN KHTN VÒNG 1
Câu $1$ : Giải phương trình nghiệm nguyên dương $(a,p,n)$ trong đó $p$ là một số nguyên tố thỏa mãn :
$$a^{2}(a^{2}+1)=5^{n}(5^{n+1}-p^{3})$$
Câu $2$ : Tìm tất cả đa thức hệ số thực thỏa mãn :
$$2(P(x)-P(\frac{1}{x}))^{2}+3P(x^{2})P(\frac{1}{x^{2}})=0$$
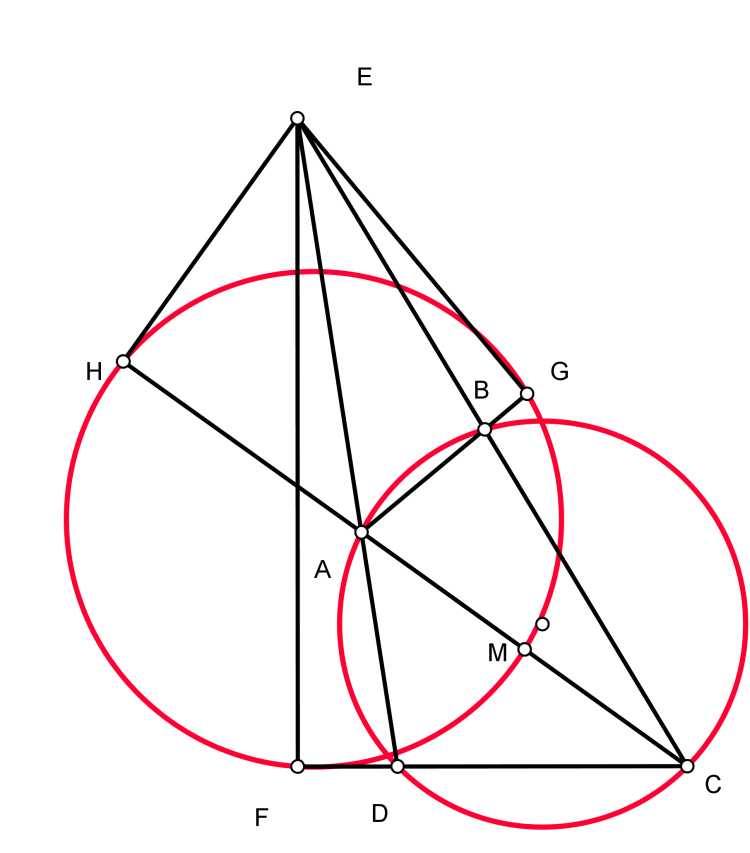
Câu $3$ : Cho tam giác $ABC$ nhọn có $AB<AC$ , $H,O$ lần lượt là trực tâm và tâm ngoại tiếp của tam giác $ABC$ . $E$ thuộc cạnh $AC$ sao cho $OE || BC$ . Gọi $OE$ cắt đường tròn ngoại tiếp tam giác $EBC$ tại $F$ . Tiếp tuyến tại $F$ của đường tròn $(EBC)$ cắt $BC,AH$ lần lượt ở $P,Q$ .
$a)$ Chứng minh đường tròn $(K)$ ngoại tiếp tam giác $BPQ$ đi qua trung điểm $M$ của $AH$
$b)$ Gọi $PA,PH$ cắt $(K)$ ở $S,T$ khác $P$ . Chứng minh rằng hai tiếp tuyến tại $S,T$ của $K$ cắt nhau trên $ME$
Câu $4$ : Một số nguyên dương $n \geq 2$ được gọi là tốt nếu với mọi $2 \leq k \leq n$ thì $n$ có dạng $n = a_{1}+a_{2}+....+a_{k}$ trong đó $(n,a_{k})=1$ và các số $a_{i}$ là nguyên dương . Tính tổng tất cả các số tốt nhỏ hơn $2016$
![]() làm khá là chán , mọi người vào chém đi .
làm khá là chán , mọi người vào chém đi .
Bài viết đã được chỉnh sửa nội dung bởi bangbang1412: 17-09-2016 - 20:04