thể tích của khối hai mươi mặt đều cạnh a=1 là bao nhiêu

thể tích của khối hai mươi mặt đều cạnh a=1 là bao nhiêu
#1
 Đã gửi 03-10-2016 - 22:42
Đã gửi 03-10-2016 - 22:42

#2
 Đã gửi 05-10-2016 - 21:35
Đã gửi 05-10-2016 - 21:35

Bài viết đã được chỉnh sửa nội dung bởi vkhoa: 05-10-2016 - 22:38
- diephu yêu thích
(Giúp với Tính $\int_m^n\left(\sqrt{ax^4 + bx^3 + cx^2 + dx + e}\right) dx$)
(Tam giác ABC cân tại A, lấy D trên cạnh BC, r1,r2 là bán kính nội tiếp ABD, ACD. Xác định vị trí D để tích r1.r2 lớn nhất )
(Nhấn nút "Thích" thay cho lời cám ơn, nút Thích nằm cuối mỗi bài viết, đăng nhập để nhìn thấy nút Thích)
#4
 Đã gửi 14-11-2016 - 07:51
Đã gửi 14-11-2016 - 07:51

Bạn nói đúng, tôi tính SO saiKhông biết là nên gọi là thầy cô hay bạn nhưng tác giả nên xem lại lời giải. Đáp số không đúng
(Giúp với Tính $\int_m^n\left(\sqrt{ax^4 + bx^3 + cx^2 + dx + e}\right) dx$)
(Tam giác ABC cân tại A, lấy D trên cạnh BC, r1,r2 là bán kính nội tiếp ABD, ACD. Xác định vị trí D để tích r1.r2 lớn nhất )
(Nhấn nút "Thích" thay cho lời cám ơn, nút Thích nằm cuối mỗi bài viết, đăng nhập để nhìn thấy nút Thích)
#5
 Đã gửi 31-12-2016 - 21:57
Đã gửi 31-12-2016 - 21:57

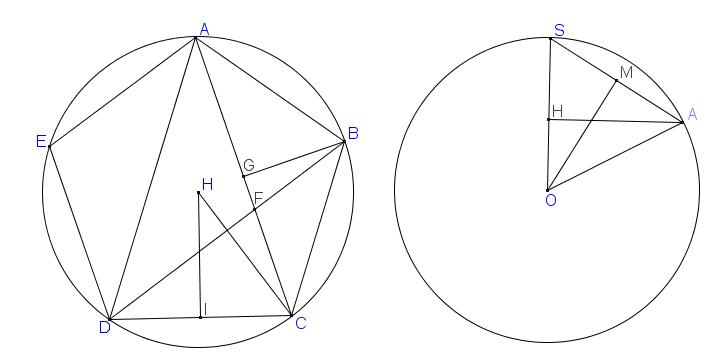
Xét ngũ giác đều ABCDE có cạnh =1 và có tâm ngoại tiếp là HG, I lần lượt là trung điểm AC, DCAC và BD cắt nhau tại Fđặt AC =dtam giác ADC có DF là phân giác$\Rightarrow\frac{DC}{FC} =\frac{DA}{FA} =\frac{DC +DA}{FC +FA} =\frac{1 +d}d$ (1)có $\triangle CDF\sim\triangle CAD$ (g, g)$\Rightarrow \frac{DC}{FC} =\frac{AC}{DC} =d$ (2)từ (1, 2)$\Rightarrow d =\frac{1 +\sqrt{5}}2$$\Rightarrow GB =\sqrt{\frac{5 -\sqrt{5}}8}$$\triangle HIC \sim\triangle AGB$ (g, g)$\Rightarrow HC =\sqrt{\frac2{5 -\sqrt{5}}}$5 mặt có một điểm chung của hình khối tại thành hình chóp ngũ giác đều S.ABCDE có cạnh bên =cạnh đáy, H là tâm ngoại tiếp ABCDEcó SH vuông góc HA$\Rightarrow SH^2 =SA^2 -HA^2 =1 -\frac2{5 -\sqrt{5}} =\frac{5 -\sqrt{5}}{10}$gọi O là tâm khối 20 mặt đều, gọi M là trung điểm SAcó $\triangle SMO\sim\triangle SHA$ (g, g)$\Rightarrow \frac{SO}{SM} =\frac{SH}{SA}$$\Rightarrow SO =\frac14 .\sqrt{2(5 +\sqrt{5})}$gọi J là tâm đường tròn ngoại tiếp SAB$JS =\frac{\sqrt{3}}3$$OJ^2 =OS^2 -JS^2 =\frac{7 +3\sqrt{5}}{24}$$\Rightarrow $thể tích =$\frac{5\sqrt{14 +6\sqrt{5}}}3$
Không biết là nên gọi là thầy cô hay bạn nhưng tác giả nên xem lại lời giải. Đáp số không đúng
Bạn nói đúng, tôi tính SO sai
Tôi vừa tính toán lại, chỗ kết quả SO là đúng, nhưng tỉ lệ đồng dạng gõ sai, phải là $ \frac{SO}{SM} =\frac{SA}{SH}$
còn thể tích phải =$\frac{5\sqrt{14+6\sqrt{5}}}{12}$
- chanhquocnghiem và leminhnghiatt thích
(Giúp với Tính $\int_m^n\left(\sqrt{ax^4 + bx^3 + cx^2 + dx + e}\right) dx$)
(Tam giác ABC cân tại A, lấy D trên cạnh BC, r1,r2 là bán kính nội tiếp ABD, ACD. Xác định vị trí D để tích r1.r2 lớn nhất )
(Nhấn nút "Thích" thay cho lời cám ơn, nút Thích nằm cuối mỗi bài viết, đăng nhập để nhìn thấy nút Thích)
#6
 Đã gửi 01-01-2017 - 15:47
Đã gửi 01-01-2017 - 15:47

thể tích của khối hai mươi mặt đều cạnh a=1 là bao nhiêu
Ôi, xin lỗi, là mình nhầm.
Bạn @vkhoa tính đúng rồi !
Bài viết đã được chỉnh sửa nội dung bởi chanhquocnghiem: 01-01-2017 - 18:39
- leminhnghiatt yêu thích
...
Ðêm nay tiễn đưa
Giây phút cuối vẫn còn tay ấm tay
Mai sẽ thấm cơn lạnh khi gió lay
Và những lúc mưa gọi thương nhớ đầy ...
#7
 Đã gửi 12-01-2017 - 16:30
Đã gửi 12-01-2017 - 16:30

Xét ngũ giác đều ABCDE có cạnh =1 và có tâm ngoại tiếp là HG, I lần lượt là trung điểm AC, DCAC và BD cắt nhau tại Fđặt AC =dtam giác ADC có DF là phân giác$\Rightarrow\frac{DC}{FC} =\frac{DA}{FA} =\frac{DC +DA}{FC +FA} =\frac{1 +d}d$ (1)có $\triangle CDF\sim\triangle CAD$ (g, g)$\Rightarrow \frac{DC}{FC} =\frac{AC}{DC} =d$ (2)từ (1, 2)$\Rightarrow d =\frac{1 +\sqrt{5}}2$$\Rightarrow GB =\sqrt{\frac{5 -\sqrt{5}}8}$$\triangle HIC \sim\triangle AGB$ (g, g)$\Rightarrow HC =\sqrt{\frac2{5 -\sqrt{5}}}$5 mặt có một điểm chung của hình khối tại thành hình chóp ngũ giác đều S.ABCDE có cạnh bên =cạnh đáy, H là tâm ngoại tiếp ABCDEcó SH vuông góc HA$\Rightarrow SH^2 =SA^2 -HA^2 =1 -\frac2{5 -\sqrt{5}} =\frac{5 -\sqrt{5}}{10}$gọi O là tâm khối 20 mặt đều, gọi M là trung điểm SAcó $\triangle SMO\sim\triangle SHA$ (g, g)$\Rightarrow \frac{SO}{SM} =\frac{SH}{SA}$$\Rightarrow SO =\frac14 .\sqrt{2(5 +\sqrt{5})}$gọi J là tâm đường tròn ngoại tiếp SAB$JS =\frac{\sqrt{3}}3$$OJ^2 =OS^2 -JS^2 =\frac{7 +3\sqrt{5}}{24}$$\Rightarrow $thể tích =$\frac{5\sqrt{14 +6\sqrt{5}}}3$
Xin hỏi tác giả thêm một chút, là sau khi tính được AC, SO, OJ,.... thì thể tích được tính bằng công thức nào vậy? Liệu có công thức tính thể tích của khối đa diện này không ? hay phải chia ra từng khối nhỏ, mà nếu chia ra từng khối nhỏ thì chia như thế nào? Thanks.
#8
 Đã gửi 13-01-2017 - 17:05
Đã gửi 13-01-2017 - 17:05

Xin hỏi tác giả thêm một chút, là sau khi tính được AC, SO, OJ,.... thì thể tích được tính bằng công thức nào vậy? Liệu có công thức tính thể tích của khối đa diện này không ? hay phải chia ra từng khối nhỏ, mà nếu chia ra từng khối nhỏ thì chia như thế nào? Thanks.
Ta tính được :
$OJ=\sqrt{\frac{7+3\sqrt{5}}{24}}$
$S_{SAB}=\frac{\sqrt{3}}{4}$
$V_{O.SAB}=\frac{S_{SAB}.OJ}{3}=\frac{\sqrt{14+6\sqrt{5}}}{48}$
$\Rightarrow$ Thể tích khối 20 mặt đều là :
$V=20\ V_{O.SAB}=\frac{5\sqrt{14+6\sqrt{5}}}{12}$.
- diephu yêu thích
...
Ðêm nay tiễn đưa
Giây phút cuối vẫn còn tay ấm tay
Mai sẽ thấm cơn lạnh khi gió lay
Và những lúc mưa gọi thương nhớ đầy ...
#9
 Đã gửi 13-01-2017 - 21:53
Đã gửi 13-01-2017 - 21:53

Cảm ơn bạn nhiều. Nhưng mình tự hỏi liệu có chứng mình được một công thức tính thể tích mà chỉ phụ thuộc a (cạnh của đa diện) không nhỉ.
Ta tính được :
$OJ=\sqrt{\frac{7+3\sqrt{5}}{24}}$
$S_{SAB}=\frac{\sqrt{3}}{4}$
$V_{O.SAB}=\frac{S_{SAB}.OJ}{3}=\frac{\sqrt{14+6\sqrt{5}}}{48}$
$\Rightarrow$ Thể tích khối 20 mặt đều là :
$V=20\ V_{O.SAB}=\frac{5\sqrt{14+6\sqrt{5}}}{12}$.
Bài viết đã được chỉnh sửa nội dung bởi diephu: 13-01-2017 - 21:55
#10
 Đã gửi 14-01-2017 - 10:50
Đã gửi 14-01-2017 - 10:50

Cảm ơn bạn nhiều. Nhưng mình tự hỏi liệu có chứng mình được một công thức tính thể tích mà chỉ phụ thuộc a (cạnh của đa diện) không nhỉ.
Nếu cạnh khối $20$ mặt đều là $a$ thì bằng cách hoàn toàn tương tự, ta tính được :
$OJ=\sqrt{\frac{7+3\sqrt{5}}{24}}\ a$
$S_{SAB}=\frac{\sqrt{3}}{4}\ a^2$
$V_{O.SAB}=\frac{S_{SAB}.OJ}{3}=\frac{\sqrt{14+6\sqrt{5}}}{48}\ a^3$
$\Rightarrow$ Thể tích khối 20 mặt đều là :
$V=20\ V_{O.SAB}=\frac{5\sqrt{14+6\sqrt{5}}}{12}\ a^3$.
Bài viết đã được chỉnh sửa nội dung bởi chanhquocnghiem: 14-01-2017 - 10:52
...
Ðêm nay tiễn đưa
Giây phút cuối vẫn còn tay ấm tay
Mai sẽ thấm cơn lạnh khi gió lay
Và những lúc mưa gọi thương nhớ đầy ...
#11
 Đã gửi 16-01-2017 - 21:19
Đã gửi 16-01-2017 - 21:19

Xét ngũ giác đều ABCDE có cạnh =1 và có tâm ngoại tiếp là HG, I lần lượt là trung điểm AC, DCAC và BD cắt nhau tại Fđặt AC =dtam giác ADC có DF là phân giác$\Rightarrow\frac{DC}{FC} =\frac{DA}{FA} =\frac{DC +DA}{FC +FA} =\frac{1 +d}d$ (1)có $\triangle CDF\sim\triangle CAD$ (g, g)$\Rightarrow \frac{DC}{FC} =\frac{AC}{DC} =d$ (2)từ (1, 2)$\Rightarrow d =\frac{1 +\sqrt{5}}2$$\Rightarrow GB =\sqrt{\frac{5 -\sqrt{5}}8}$$\triangle HIC \sim\triangle AGB$ (g, g)$\Rightarrow HC =\sqrt{\frac2{5 -\sqrt{5}}}$5 mặt có một điểm chung của hình khối tại thành hình chóp ngũ giác đều S.ABCDE có cạnh bên =cạnh đáy, H là tâm ngoại tiếp ABCDEcó SH vuông góc HA$\Rightarrow SH^2 =SA^2 -HA^2 =1 -\frac2{5 -\sqrt{5}} =\frac{5 -\sqrt{5}}{10}$gọi O là tâm khối 20 mặt đều, gọi M là trung điểm SAcó $\triangle SMO\sim\triangle SHA$ (g, g)$\Rightarrow \frac{SO}{SM} =\frac{SH}{SA}$$\Rightarrow SO =\frac14 .\sqrt{2(5 +\sqrt{5})}$gọi J là tâm đường tròn ngoại tiếp SAB$JS =\frac{\sqrt{3}}3$$OJ^2 =OS^2 -JS^2 =\frac{7 +3\sqrt{5}}{24}$$\Rightarrow $thể tích =$\frac{5\sqrt{14 +6\sqrt{5}}}3$
vẽ hình như thế nào vậy ạ
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Chờ hoài mà trời không sập
Chờ hoài mà trời không sập ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh