Bài $5$: (7,0 điểm) Tìm tất cả các hàm số $f: \mathbb{R} \rightarrow \mathbb{R}$ thỏa mãn các điều kiện:
$i)$ $f(1)>0$
$ii)$ $f(xy-1)+2f(x)f(y)=3xy-1$ $\forall x,y \in \mathbb{R}$
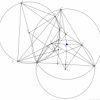
Bài $6$: (6,0 điểm) Cho $\triangle ABC$. $M$ là điểm chuyển động trên cạnh $AC$. Đường tròn ngoại tiếp $\triangle ABM$ cắt cạnh $BC$ tại điểm thứ hai là $D$, đường tròn ngoại tiếp $\triangle BCM$ cắt cạnh $AB$ tại điểm thứ hai là $E$.
$a)$ Gọi $O$ là giao điểm của $AD$ và $CE$. Chứng minh rằng 4 điểm $A,E,O,M$ cùng thuộc 1 đường tròn.
$b)$ Gọi $I,J,N$ lần lượt là giao điểm của các cặp đường thẳng $AB$ và $DM$, $BC$ và $EM$, $AJ$ và $CI$. Chứng minh $MN$ luôn đi qua điểm cố định.
Bài $7$: (7,0 điểm) Tìm các số nguyên dương $a,b,c,d$ thỏa mãn:
$a+2^b+3^c=3d!+1$,
biết rằng tồn tại các số nguyên tố $p,q$ sao cho
$a=(p+1)(2p+1)=(q+1)(q-1)^2$