ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
LỚP 12 TRUNG HỌC PHỔ THÔNG NĂM HỌC 2016-2017
Môn : TOÁN
Thời gian: 180 phút ( không kể phát đề)
Câu 1 :
a) Cho hàm số $y = 2{x^4} - {m^2}{x^2} + {m^2} + 2016\,\,\,\,\,(C)$ ( m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số (C ) có ba điểm cực trị A,B,C sao cho bốn điềm O,A,B,C là bốn đỉnh của một hình thoi ( Vối O là gốc tọa độ).
b) Giải hệ phương trình :$\left\{ \begin{array}{l}{x^3} - {y^3} + 6{y^2} + 2(x - 7y) + 12 = 0\\\sqrt {3 - x} + \sqrt {y - 3} = {x^2} + {y^2} - 10x - 5y + 22\end{array} \right.(x;y \in \mathbb{R} )$
Câu 2:
a) Cho khai triển ${(1 - 2x + {x^3})^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + + {a_{3n}}{x^{3n}}$ . Xác định hệ số ${a_6}$ biết rằng ${(1 - 2x + {x^3})^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + + {a_{3n}}{x^{3n}}$
b) Cho phương trình:${x^5} - \frac{1}{2}{x^4} - 5{x^3} + {x^2} + 4x - 1 = 0\,\,\,\,\,\,\,\,\,\,(*)$
b1) Chứng minh rằng phương trình (*) có đúng 5 nghiệm phân biệt.
b2) Với ${x_i}\,\,(i = \overline {1,5} )$ là nghiệm của phương trình (*), tính tổng S biết: $S = \sum\limits_{i = 1}^5 {\frac{{{x_i} + 1}}{{2x_{_i}^5 - x_i^4 - 2}}} $
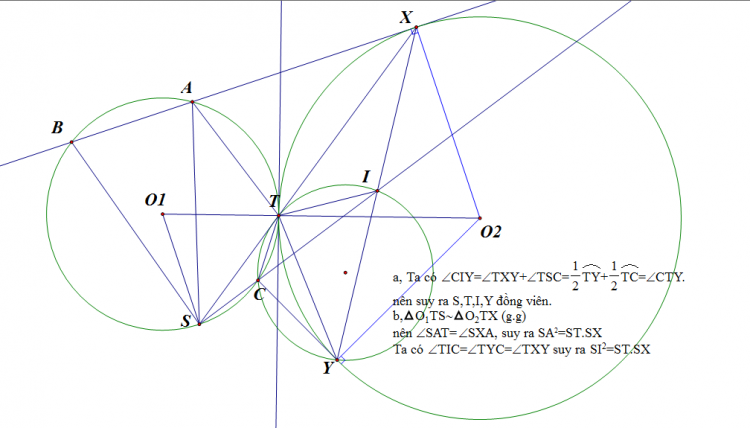
Câu 3: Cho đường tròn $({O_1}),({O_2})$ tiếp xúc ngoài tại điểm T. Một đường thẳng cắt đường tròn $({O_1})$ tại hai điểm A,B phân biệt và tiếp xúc với $({O_2})$ tại X. đường thẳng XT cắt $({O_1})$ Tại S ( S khác T và C là một điểm trên cung TS không chứa A và B. Cho CY là tiếp tuyến của $({O_2})$ tại Y sao cho các đoạn thẳng CY và ST không cắt nhau. Cho I là giao điển của các đường thẳng XY và SC. Chứng minh rằng:
a) C,T,Y và I cùng thuộc một đường tròn.
b) SA= SI
Câu 4: Cho $a,b,c$ là các số thực dương . Tìm giá trị nhỏ nhất của biểu thức:
$P = \frac{{1344}}{{a + \sqrt {ab} + \sqrt[3]{{abc}}}} - \frac{{2016}}{{\sqrt {a + b + c} }}$
Câu 5: Cho p là số nguyên tố lẻ và $T = \sum\limits_{k = 0}^p {C_p^kC_{p + k}^k} - ({2^p} + 1)$. Chứng minh rằng T chia hết cho ${p^2}$ .
Bài viết đã được chỉnh sửa nội dung bởi Dinh Xuan Hung: 13-10-2016 - 21:18