Chủ đề này có 2 trả lời

[hoangtubatu955]

Với mọi số nguyên dương $n$, kí hiệu $S(n)$ là tổng các chữ số của $n^2+1$.

Xây dựng dãy $(a_n)$ như sau: $a_0 \in \mathbb{N}$ nào đó. $a_{n+1}=S(a_n); \forall n \in \mathbb{N}$.

Chứng minh rằng dãy $a_n$ tuần nào từ một số hạng thứ $n_0$ nào đó, tức chứng minh rằng tồn tại $k,n_0 \in \mathbb{N}$ sao cho $a_{n+k}=a_n ; \forall n \ge n_0 $

Bài viết đã được chỉnh sửa nội dung bởi hoangtubatu955: 11-11-2016 - 08:36

[takarin1512]

]Nếu $a_1\equiv 0\left ( mod3 \right )\Rightarrow a_1^2+1\equiv 1\left ( mod3 \right )\Rightarrow a_2\equiv 1\left ( mod3 \right )\Rightarrow a_3\equiv 2\left ( mod3 \right )$. Nếu $a_1\equiv 1\left ( mod3 \right )\Rightarrow a_2\equiv 2\left ( mod3 \right )$. Lại có nếu $a_i\equiv 2\left ( mod3 \right )\Rightarrow a_{i+1}\equiv 2\left ( mod3 \right )$. Do đó với mọi số $a_1$ cho trước thì với $n\geq 3$ thì $a_n\equiv 2\left ( mod3 \right )$.

Ta xét các tường hợp sau:
Nếu $a_i\geq 100$, gọi số chũ số của $a_i$ là $m\left ( m\geq 3 \right )$, ta có số chữ số của $a_i^2+1$ nhỏ hơn $2m$, suy ra $a_{i+1}\leq 18m$, mà $a_i\geq 10^{m-1}$. Với $m\geq 3$, ta có $10^{m-1}>18m\Rightarrow a_i > a_{i+1}$

Nếu $36\leq a_i\leq 100$ thì $a_i^2+1$ có $4$ chữ số, suy ra $a_{i+1} < 9.4=36\leq a_i$

Nếu $28\leq a_i\leq 35$ thì $a_i^2+1$ có dạng $\overline{1x_1x_2x_3}$ hoặc $\overline{x_1x_2x_3}$ cho nên $a_{i+1}<3.9+1=28\leq a_i$

Do đó $\exists n_1/\forall n\geq n_1$ thì $a_n\leq 27$ và $a_n\equiv 2\left ( mod3 \right )$. Ta xét sơ đồ sau:

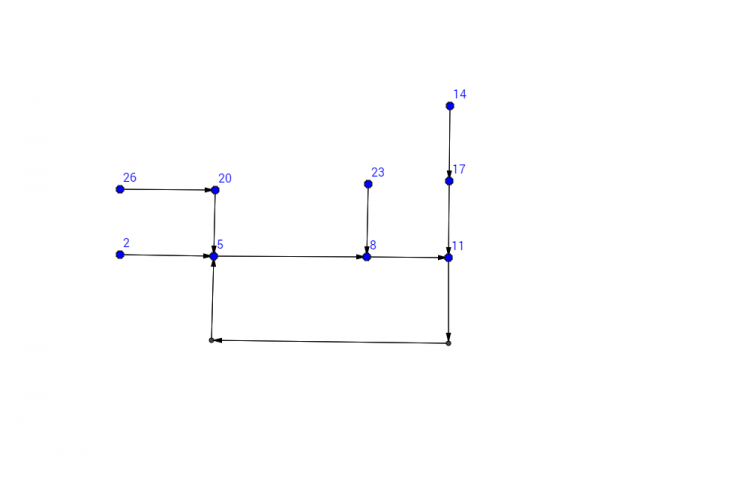
Vậy dãy sẽ luôn tuần hoàn các gía trị $5,8,11$, tức là $k=3$.

[Zaraki]

Cũng không cần phải xét chi tiết thế. Ta dùng BĐT đơn giản $s(n) \le 9 \left( \left \lfloor \log n \right \rfloor+1 \right)$ để suy ra $$a_{n+1}=s(a_n^2+1) \le 9 \left( \left \lfloor \log a_n^2+1 \right \rfloor+1 \right) < 9 \left( 2 \log a_n  +2 \right).$$

Nhận thấy rằng với $a_n \ge 100$ thì $18\log a_n+18 < a_n$ suy ra $a_{n+1} <a_n$ với $a_n \ge 100$. Ta suy ra nếu tồn tại $a_i>100$ trong dãy thì cũng sẽ tồn tại $a_j \; (j>i)$ sao cho $a_j \le 100$. 

 

Ta chứng minh rằng dãy sẽ tồn tại hai số $a_j=a_i \le 100$. Thật vậy, giả sử điều ngược lại, trong dãy có hữu hạn các số $a_i<100$ và các số này đều phân biệt. Do đó ta suy ra tồn tại $N$ sao cho $a_n>100$ với mọi $n \ge N$, điều này mâu thuẫn với điều ta vừa chứng minh trên. Như vậy sẽ tồn tại $k,n_0$ như đề bài khẳng định.