Lời giải của em ạ
Ta sẽ chứng minh bổ đề sau
Bổ đề : $\triangle ABC$, đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$.$AI$ cắt $DE,DF$ tại $M,N$. Gọi $G$ là trung điểm $BC$. Khi đó $G$ là tâm ngoại tiếp $\triangle DMN$
Chứng minh : $M$ là giao điểm của phân giác góc $\angle A$ và $DE$ nên $BM \perp AI$
Tương tự , $CN \perp AI$
Gọi $R$ là tiếp điểm của đường tròn bàng tiếp góc $\angle A$ với $BC$, $J$ là tâm bàng tiếp
Khi đó các tứ giác $JRMB, JNRC$ nội tiếp
$\implies \angle DRN = \angle MJC = \angle IBD = \angle DMN$ nên tứ giác $DMRN$ nội tiếp
Hơn nữa , $\angle DNR = \angle DNI + \angle INR = \angle DCI + \angle RCJ = 90^{\circ}$ nên $DR$ là đường kính của $(MDNR)$
$\implies G$ là tâm ngoại tiếp $(DMN)$
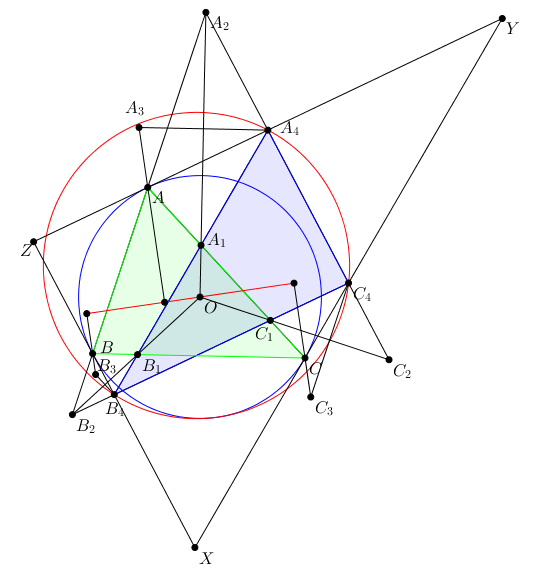
Quay lại bài toán :
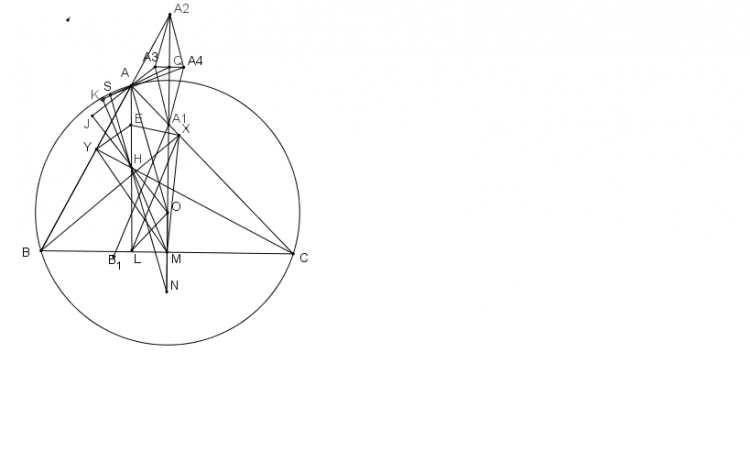
Trên trung trực đoạn $A_1A_2$ lấy điểm $A_3'$ sao cho $\triangle A_2A_3'A_1 \sim \triangle BOC$
Khi đó ta có $\angle A_3'A_2A_1 = \angle OCB $ nên $OC \perp A_3'A_2$
Tương tự ta có $OB \perp A_3'A_2$
Gọi $H$ là trực tâm $\triangle ABC$
Lại có $\triangle BHC \sim \triangle A_1AA_2 \implies \triangle A_2A_3'A_1 \cap A \sim \triangle COB \cap H$
Từ đây ta có $AA_3' \perp OH$ nên $A_3' \equiv A_3$
Nên ta có $\angle A_1A_3A_2 = \angle BOC = \angle A_2A_4A_1$ . Từ đây suy ra $A_4$ là tâm ngoại tiếp $\triangle A_1AA_2$
Tương tự ta có $B_4,C_4$ là tâm ngoại tiếp $\triangle BB_1B_2, \triangle CC_1C_2$
Có $\angle AA_4A_1 = 90^{\circ} - \angle AA_2A_1 = 90^{\circ} - \angle OAC$ nên $AA_4$ là tiếp tuyến của $(O)$ tại $A$. Tương tự ta có $BB_4,CC_4 $ cũng là tiếp tuyến của $(O)$
$AA,4,BB_4,CC_4 $ cắt nhau tạo thành $\triangle UVW$
Khi đó , $(O)$ là đường tròn nội tiếp $\triangle UVW$
Áp dụng bổ đề cho $\triangle UVW$ thì $A_4,B_4,C_4$ là trung điểm $UV,VW,WU$
Khi đó $(A_4B_4C_4)$ là đường tròn Euler của $\triangle UVW$ và $(O)$ là đường tròn nội tiếp nên $(A_4B_4C_4)$ tiếp xúc với $(O)$
Bài viết đã được chỉnh sửa nội dung bởi manhtuan00: 19-12-2016 - 12:54