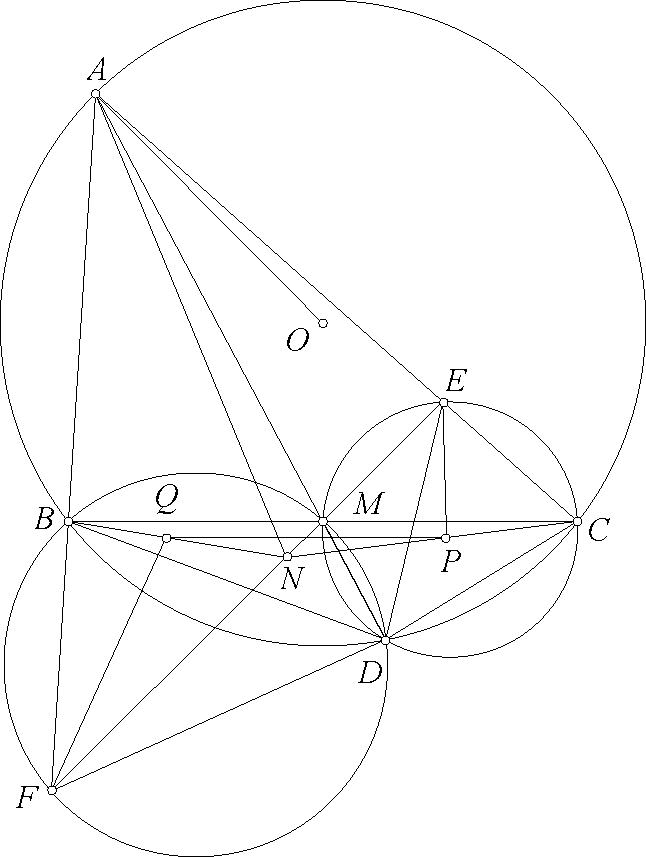Topic này là nơi dành để post các bài toán ôn tập mục đích thi vào cấp 3 chuyên toán. Một số lưu ý khi post bài như sau
- Nội dung các bài toán ở mức THCS. Ưu tiên các bài toán tứ giác nội tiếp vì chương trình thi chuyên cấp 3 hầu như chỉ xoay quanh tứ giác nội tiếp các điều kiện cần vả đủ.
- Không post bài trong các cuộc thi THCS còn hạn (như trên THTT, TTT2, PI...)
- Hạn chế hỏi bài tập về nhà.
- Post đề có nguồn gốc cụ thể.
Mình xin phép bắt đầu với một số đề hình học thi thử chuyên KHTN.
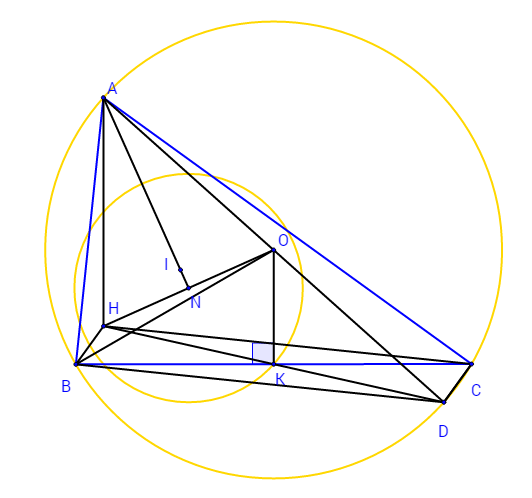
Bài toán 1 (Thi thử chuyên KHTN 2013, vòng 1, đợt 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định, $B, C$ cố định, $A$ di chuyển trên $(O)$. $D$ thuộc đoạn $BC$ sao cho $AD$ là phân giác $\angle BAC$. Đường tròn $(K)$ qua $A$ và tiếp xúc với $BC$ tại $D$.
1) Chứng minh rằng $(K)$ tiếp xúc $(O)$.
2) Gọi $(K)$ giao $CA, AB$ lần lượt tại $E, F$ khác $A$. $BE, CF$ lần lượt cắt $(K)$ tại $G, H$ khác $E, F$. $AG, AH$ cắt $BC$ lần lượt tại $M, N$. Chứng minh rằng độ dài $MN$ luôn không đổi khi $A$ di chuyển.
Bài toán 2 (Thi thử chuyên KHTN 2013, vòng 2, đợt 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. $P$ là một điểm nằm trong tam giác $ABC$. Trung trực $CA, AB$ lần lượt cắt $PA$ tại $E, F$. Đường thẳng qua $E$ song song $AC$ cắt tiếp tuyến tại $C$ của $(O)$ tại $M$. Đường thẳng qua $F$ song song $AB$ cắt tiếp tuyến tại $B$ của $(O)$ tại $N$.
1) Chứng minh rằng $MN$ tiếp xúc $(O)$.
2) Gọi $MN$ cắt dường tròn ngoại tiếp các tam giác $ACM, ABN$ lần lượt tại $Q,R$ khác $M, N$. Chứng minh rằng $BQ$ và $CR$ cắt nhau trên $(O)$.
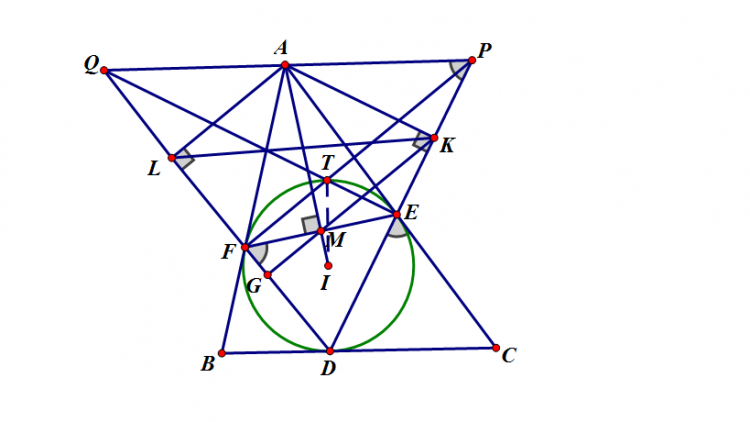
Bài toán 3 (Thi thử chuyên KHTN 2013, vòng 1, đợt 4). Cho tam giác $ABC$, đường tròn nội tiếp $(I)$ tiếp xúc $BC, CA, AB$ lần lượt tại $D, E, F$. Gọi $K, L$ lần lượt là hình chiếu của $A$ trên $DE, DF$. Gọi $IA$ giao $EF$ tại $M$.
1) Chứng minh rằng $M$ là trực tâm tam giác $DKL$.
2) Gọi $P$ đối xứng $E$ qua $K$. $Q$ đối xứng $F$ qua $L$. Chứng minh rằng $QE, PF$ cắt nhau trên đường tròn $(I)$.
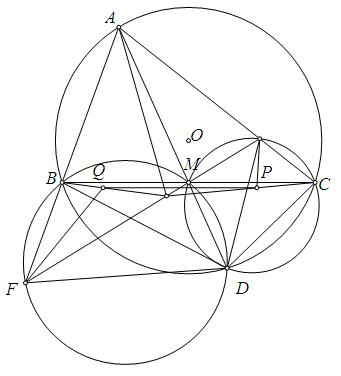
Bài toán 4 (Thi thử chuyên KHTN 2013, vòng 2, đợt 4). Cho tam giác $ABC$. Một đường tròn $(K)$ đi qua $B, C$ sao cho $(K)$ cắt đoạn $CA$ tại $E$ khác $C$ và $(K)$ cắt đoạn $AB$ tại $F$ khác $B$. $BE$ giao $CF$ tại $H$. Gọi $M$ là trung điểm $EF$. Gọi $P, Q$ lần lượt là đối xứng của $A$ qua $BE, CF$.
1) Chứng minh rằng đường tròn $(I)$ ngoại tiếp tam giác $HEP$ và đường tròn $(J)$ ngoại tiếp tam giác $HFQ$ cắt nhau trên $AM$.
2) Chứng minh rằng $(I)$ và $(J)$ có bán kinh bằng nhau.