Chủ đề này có 239 trả lời

[NHoang1608]

Bài 34: (Đề vòng 2 Chuyên Quốc Học Huế 2016-2017)

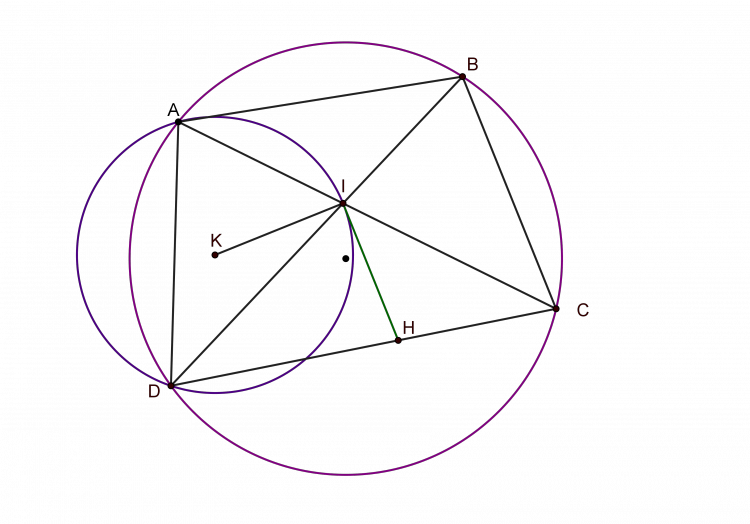
Cho hai đường tròn $(O_{1})$ và $(O_{2})$ có bán kính khác nhau, cắt nhau tại hai điểm $A$ và $B$ sao cho $O_{1}, O_{2}$ thuộc hai nửa mặt phẳng có bờ là đường thẳng $AB$. Đường tròn $(O)$ ngoại tiếp tam giác $BO_{1}O_{2}$ cắt $(O_{1})$ và $(O_{2})$ lần lượt tại $K$ và $L$ (khác $A$ và $B$). Đường thẳng $AO$ cắt $(O_{1})$ và $(O_{2})$ lần lượt tại $M$ và $N$ (khác $A$). Hai đường thẳng $MK$ và $NL$ cắt nhau tại $P$ sao cho $P$ và $B$ thuộc hai nửa mặt phẳng có bờ là đường thẳng $KL$. Chứng minh rằng

a) Tứ giác $BKPL$ nội tiếp đường tròn

b) Điểm $A$ cách đều hai đường thẳng $BK$ và $BL$

c) Điểm $P$ thuộc đường thẳng $AB$ khi và chỉ khi tam giác $PKL$ cân

$\boxed{\text{Lời giải bài 34}}$

a) Ta có $\widehat{KPL}+\widehat{KBL}=\widehat{KPL}+\widehat{KBA}+\widehat{ABL}$

                                                             $=\widehat{KPL}+\widehat{PMN}+\widehat{PNM}=180^{\circ}$

$\Rightarrow$ Tứ giác KPLB nội tiếp đường tròn $(O)$.

b) Ta có: $\widehat{AO_{2}O_{1}}=\widehat{O_{1}O_{2}B}=\widehat{O_{1}KB}=\widehat{O_{1}BK}$

             Mặt khác: Tứ giác $KO_{1}BO_{2}$ nội tiếp nên $\widehat{O_{1}BK}=\widehat{KO_{2}O_{1}}$

             Suy ra $\widehat{AO_{2}O_{1}}=\widehat{KO_{2}O_{1}}$ hay $K, A, O_{2}$ thẳng hàng.

Chứng minh tương tự ta cũng có: 3 điểm $L, A, O_{1}$ thẳng hàng.

$\widehat{LKA}=\widehat{LO_{1}O_{2}}=\frac{1}{2}\widehat{AO_{1}B}=\widehat{AKB}$

$\Rightarrow KA$ là phân giác $\widehat{BKL}$.

Tương tự ta có $LA$ là phân giác $\widehat{KLB}$

$\Rightarrow A$ là giao của 3 đường phân giác tam giác $BKL$.

$\Rightarrow AB$ là phân giác $\widehat{KBL}$ hay $A$ cách đều $BK$ và $BL$.

c) Ta sẽ chứng minh nếu $P$ thuộc đường thẳng $AB$ thi tam giác $KPL$ cân.

Ta có: $\widehat{PKL}=\widehat{KBA}=\widehat{ABL}=\widehat{PLK}$ ( Vì $AB$ là phân giác $\widehat{KBL}$)

           $\Rightarrow$ Tam giác $KPL$ cân tại $P$.

Nếu tam giác $KPL$ cân thì $P$ thuộc đường thẳng $AB$.

Vì $\widehat{PMN}=\widehat{KBA}=\widehat{ABL}=\widehat{PNA}$ 

    $\Rightarrow$ Tam giác $PMN$ cân tại $P$ mà tam giác $KPL$ cân nên $KL//MN$

Ta có $\widehat{PKL}=\widehat{PMN}=\widehat{KBA}=\widehat{ABL}$

         Mặt khác tứ giác $BLPK$ nội tiếp nên $\widehat{PKL}=\widehat{PBL}$

Suy ra $\widehat{ABL}=\widehat{PBL}$ hay $P$ thuộc đường thẳng $AB$.

Vậy bài toán chứng minh xong.

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 29-03-2017 - 17:30

[NHoang1608]

Bài toán đề xuất tiếp theo:

Bài 38: (Đề vòng 2 trường THPT Chuyên Vĩnh Phúc năm 2013-2014).

Cho tam giác nhọn $ABC$ ($AB<AC$). Các đường cao $AD,BE,CF$ của tam giác $ABC$. Gọi $P$ là giao điểm của đường thẳng $BC$ và $EF$. Đường thẳng qua $D$ song song với $EF$ lần lượt cắt các đường thẳng $AB, AC, CF$ tại $Q, R, S$. Chứng minh rằng:

1. Tứ giác $BQCR$ nội tiếp.

2. $\frac{PB}{PC}=\frac{DB}{DC}$ và $D$ là trung điểm của $QS$.

3.Đường tròn ngoại tiếp tam giác $PQR$ đi qua trung điểm $BC$

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 05-04-2017 - 13:07

[Nguyenphuctang]

Bài toán đề xuất tiếp theo:

Bài 38: (Đề vòng 2 trường THPT Chuyên Đại Học Sư Phạm Hà Nội năm 2015-2016).

Cho tam giác nhọn $ABC$ ($AB<AC$), $M$ là trung điểm của cạnh $BC$, $O$ là tâm đường tròn ngoại tiếp tam giác. Các đường cao $AD,BE,CF$ của tam giác $ABC$ đồng quy tại $H$. Các tiếp tuyến với $(O)$ tại $B$ và $C$ cắt nhau tại $S$. Gọi $X,Y$ lần lượt là các giao điểm của đường thẳng $EF$ với các đường thẳng $BS,AO$. Chứng minh rằng:

1. $MX \perp BF$

2. Hai tam giác $SMX$ và $DHF$ đồng dạng 

3.$\frac{EF}{FY}=\frac{BC}{CD}$

Xem kĩ nhé bài này trùng với bài 11. Lần sau cũng nên xem kĩ trước khi đăng tránh tình trạng loãng topic .

[diemdaotran]

$\boxed{39}$ (đề thi vào chuyên toán thpt chuyên đhsp)

Cho tứ giác lồi ABCD, trung tuyến AM của ABC, trung tuyến AN của tam giác ADC. Chứng minh $S_{ABCD}\leq\frac{1}{2}(AM+AN)^2$

p/s: đề lâu lắm rồi cũng không nhớ năm bao nhiêu

[Nguyenphuctang]

Lời giải khác cho bài 36: 

[trambau]

Cho $\Delta ABC$ ngoại tiếp $(I)$, điểm $D$ thuộc $BC$ , đường tròn $(I_{1})$ và $(I_{2})$ nội tiếp 2 tam giác $ABD$ và $ACD$. Vẽ tiếp tuyến chung ngoài khác $BC$ của $(I_{1})$ và $(I_{2})$ cắt $AD$ tại $M$, $(I)$ tiếp xúc với $AC,AB$ tại $E,F$. chứng minh $AM=AE=AF$

 

[Minhnksc]

Cho $\Delta ABC$ ngoại tiếp $(I)$, điểm $D$ thuộc $BC$ , đường tròn $(I_{1})$ và $(I_{2})$ nội tiếp 2 tam giác $ABD$ và $ACD$. Vẽ tiếp tuyến chung ngoài khác $BC$ của $(I_{1})$ và $(I_{2})$ cắt $AD$ tại $M$, $(I)$ tiếp xúc với $AC,AB$ tại $E,F$. chứng minh $AM=AE=AF$

 

Gọi S;R lần lượt là tiếp điểm của $(I_{1})$ và $(I_{2})$ với $AD$, tiếp tuyến chung của $(I_{1})$ và $(I_{2})$ lần lượt tiếp xúc với $(I_{1})$ và $(I_{2})$ $P$ và $Q$, $BC$ tiếp xúc với $(I_{1})$ và $(I_{2})$ tại G và H

Ta có $MP=MS; MQ = MR \Rightarrow AS+AR=PQ+2AM$(1)

Dễ thấy $PQ=GH=GD+DH=\frac{AD+BD-AB}{2}+\frac{AD+CD-AC}{2}=AD+\frac{BC-AB-AC}{2}$

             $AS+AR=\frac{AD+AB-BD}{2}+\frac{AD+AC-CD}{2}=AD+\frac{AB+AC-BC}{2}$

Kết hợp với (1), ta có $AM=\frac{AB+AC-BC}{2}$

Mà $AE=AF=\frac{AB+AC-BC}{2}$

$\Rightarrow AM=AE=AF$.

P/s: chị nhớ ghi số bài và cả nguồn (nếu có) nhé

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 30-03-2017 - 21:08

[NTMFlashNo1]

Bài 39: (Thi thử chuyên $KHTN-2011$)

Cho $(O)$ đường kính $AB$.Đường thẳng $d$ tiếp xúc $(O)$ tại $A$. $I$ cố định trên $AB$. $DE$ là dây cung thay đổi của $(O)$ luôn đi qua $I$. $BD,BE$ cắt $d$ tại $M,N$.Chứng minh:

a) $DENM$ nội tiếp

b) $AM.AN$ không đổi 

c) Tâm đường tròn ngoại tiếp $DENM$ thuộc đường tròn cố định.

 

 

 

$\boxed{39}$ (đề thi vào chuyên toán thpt chuyên đhsp)

Cho tứ giác lồi ABCD, trung tuyến AM của ABC, trung tuyến AN của tam giác ADC. Chứng minh $S_{ABCD}\leq\frac{1}{2}(AM+AN)^2$

p/s: đề lâu lắm rồi cũng không nhớ năm bao nhiêu

Vấn đề của bạn khá "cũ" xem như đây là bài để tham khảo.

[Minhnksc]

Bài 39: (Thi thử chuyên $KHTN-2011$)

Cho $(O)$ đường kính $AB$.Đường thẳng $d$ tiếp xúc $(O)$ tại $A$. $I$ cố định trên $AB$. $DE$ là dây cung thay đổi của $(O)$ luôn đi qua $I$. $BD,BE$ cắt $d$ tại $M,N$.Chứng minh:

a) $DENM$ nội tiếp

b) $AM.AN$ không đổi 

c) Tâm đường tròn ngoại tiếp $DENM$ thuộc đường tròn cố định.

 

 

 

 

BÀI 39:
a, ta có $BD.BM=AB^2$ và $BE.BN=AB^2$ nên $BD.BM=BE.BN$ và suy ra tứ giác $DENM$ nội tiếp

b, Gọi giao điểm của đường tròn ngoại tiếp $\Delta MBN$ với AB là K

vì $\angle{KNB}=\angle{KNM}+\angle{MNB}=\angle{DBA}+\angle{BAE}=\angle{AEI}+\angle{IAE}=\angle{BIE}$

$\Rightarrow KIEN $ nội tiếp $\Rightarrow BI.BK=BE.BN=AB^2$

mà $I$ cố định; $AB$ cố định nên $K$ cố định

lại có $AK.AB=AM.AN$ nên suy ra đpcm

c,Gọi giao điểm của đường tròn ngoại tiếp  tứ giác $DENM$ với đường thẳng AB là $L$ và $J$ ( J nằm giữa A và B)(1)

vì $AM.AN =AL.AJ$ nên $AL.AJ$ cố định

kẻ dây  PQ vuông góc với AB tại I, BQ  và BP cắt d lần lượt ở R và S

theo câu a, ta có $AM.AN=AR.AS \Rightarrow AL.AJ=AR.AS \Rightarrow RJSL$ nội tiếp

ta thấy $BL.BJ=BQ.BR(=AB^2)$ nên Q thuộc đường tròn ngoại tiếp tứ giác RJSL hay J và L là giao điểm của đường tròn ngoại tiếp tam giác RSQ với đường thẳng AB $\Rightarrow$ J và L cố định

do đó, kết hợp với (1) suy ra tâm đường tròn ngoại tiếp DENM chuyển động trên đường trung trực của JL 

 

bạn xem đề bài có sai gì không chứ câu c nó là đường thẳng cố định chứ không phải đường tròn cố định

P/s: giống đề hsg Bắc Giang năm nay nhỉ.

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 02-04-2017 - 23:10

[Nguyenphuctang]

Bài 40: (Diễn đàn AoPS)

Cho tứ giác $ABCD$ nội tiếp $(O)$ có hai đường chéo cắt nhau tại $I$. Gọi $K$ là tâm $(IAD)$. Cmr: $IK$ vuông $BC$

[Minhnksc]

Bài 40: (Diễn đàn AoPS)

Cho tứ giác $ABCD$ nội tiếp $(O)$ có hai đường chéo cắt nhau tại $I$. Gọi $K$ là tâm $(IAD)$. Cmr: $IK$ vuông $BC$

gọi giao điểm của đường thẳng $IK$ và $BC$ là $H$

Trong 2 góc IAD và IDA, có ít nhất 1 góc nhọn, giả sử góc IAD nhọn

Khi này, vì $K$ là tâm $(IAD)$ nên $\angle{DKI}=2\angle{DAI}=2\angle{IBC}$(1)

mà $\Delta IKD$ cân tại $K$ nên $\angle{KID}=90^0-\frac{\angle{DKI}}{2}$

kết hợp với (1) ta có: $\angle{KID}=90^0-\angle{IBC}\Rightarrow \angle{BIH}=90^0-\angle{IBH}$

từ đó suy ra đpcm.

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 04-04-2017 - 21:40

[Nguyenphuctang]

geogebra-export (13).png

gọi giao điểm của đường thẳng $IK$ và $BC$ là $H$

vì $K$ là tâm $(IAD)$ nên $\angle{DKI}=2\angle{DAI}=2\angle{IBC}$(1)

mà $\Delta IKD$ cân tại $K$ nên $\angle{KID}=90^0-\frac{\angle{DKI}}{2}$

kết hợp với (1) ta có: $\angle{KID}=90^0-\angle{IBC}\Rightarrow \angle{BIH}=90^0-\angle{IBH}$

từ đó suy ra đpcm

Yêu cầu bạn ghi rõ ra nhé chỗ (1) chứng minh cũng không phải dễ. Vẫn còn cách khác nhẹ nhàng hơn nhiều 

[Minhnksc]

Bài 41:(mở rộng bài 40)Cho đường tròn $(O)$ cố định và T cố định nằm trong $(O)$, hai dây $AB$ và $CD$ của $(O)$ quay quanh $T$, gọi $K$ và $J$ lần lượt là tâm của $(TAD)$ và $(TBC)$. Chứng minh $KJ$ luôn đi qua một điểm cố định khi $AB$ và $CD$ thay đổi

[Nguyenphuctang]

Có vẻ cách trên của bài 40 đơn giản nhỉ? Sau đây tôi xin trình bày 1 số cách khác cho bài 40:

Cách 1: Của Iceghost

Qua $I$ kẻ đường thẳng song song với $BC$ cắt $CD$ tại $H$.

Ta có:

$\angle DIH = \angle DBC =\angle DAC$ Suy ra $IH$ là tiếp tuyến của $(K)$ 

$\Rightarrow IH \perp KI; IH//BC\Rightarrow KI \perp BC$

Cách 2: của mình.

Gọi $J=KI \cap BC;M =AC \cap OK$.

Dễ thấy: $OK$ là đường trun trực của AD.

Ta có:

$\angle KDM =\angle KIA =\angle KAI \Rightarrow KIMD $ nội tiếp. $\Rightarrow  \angle DAM + \angle AMK =90 \Rightarrow  \angle BIJ +\angle IBC =90.$

$\Rightarrow  KI \perp BC.$

 

[Nguyenphuctang]

 

Capture.PNG

 

a, Vì $EF \parallel RQ$ nên $\angle BQR=\angle AFE=\angle RCB$ suy ra $BQCR$ nội tiếp.

 

b, Dễ thấy $EB, EC$ lần lượt là phân giác trong và phân giác ngoài đỉnh $E$ của tam giác $EDP,$ do đó 

\[\frac{BD}{BP}=\frac{ED}{EP}=\frac{CD}{CP}\]

Chú ý rằng $QS \parallel PF$ nên theo Thales $\frac{DQ}{PF}=\frac{BD}{BP}=\frac{CD}{CP}=\frac{DS}{PF},$ thành thử $DQ=DS.$

 

c, Gọi $M$ là trung điểm của $BC,$ ta có $EMDF$ nội tiếp, từ đó $\triangle PDF \sim \triangle EDM \mbox{ (g.g)}$ suy ra $DP.DM=DE.DF$

Ta có $\angle DQF=\angle AFE =\angle DFQ$ suy ra $DQ=DF,$ tương tự $DE=DR.$

Bởi vậy $DP.DM=DE.DF=DQ.DR$ suy ra $PQMR$ nội tiếp hay $(PQR)$ đi qua $M.$

Câu b:Để chứng minh: $\frac{PB}{PC}=\frac{DB}{DC}$ ta có cách khác và đó là 1 bổ đề rất quan trọng:

Cho tam giác $ABC$ và các điểm $D,E,F$ lần lượt thuộc BC,CA,AB sao cho $AD, BE, CF$ đồng quy. Giả sử $EF \cap BC=S$ Chứng minh rằng: $\frac{DB}{DC} = \frac{SB}{SC}$. Chứng minh:

Áp dụng định lí $Ceva$: $\frac{DB.AE.FB}{DC.EC.FA}=1$. Tiếp tục áp dụng định lí $Menelaus$ cho cát tuyến $S,E,F $ thì : $\frac{SC.EA.FB}{SB.EC.FA}=1$.

Từ đó suy ra điều phải chứng minh.

Câu c: Áp dụng hệ thức $Maclaurin$ cho hàng điểm điều hòa $DPBC$ ta có: $DP.DM=DB.DC=DQ.DR$. 

Ngoài ra ta có thể mở rộng lên cho 3 đường đồng quy vẫn được không nhất thiết phải là đường cao. 

Bài viết đã được chỉnh sửa nội dung bởi Nguyenphuctang: 05-04-2017 - 12:49

[Minhnksc]

Có vẻ cách trên của bài 40 đơn giản nhỉ? Sau đây tôi xin trình bày 1 số cách khác cho bài 40:

Cách 1: Của Iceghost

aops 1.png

Qua $I$ kẻ đường thẳng song song với $BC$ cắt $CD$ tại $H$.

Ta có:

$\angle DIH = \angle DBC =\angle DAC$ Suy ra $IH$ là tiếp tuyến của $(K)$ 

$\Rightarrow IH \perp KI; IH//BC\Rightarrow KI \perp BC$

Cách 2: của mình.

aops 2.png

Gọi $J=KI \cap BC;M =AC \cap OK$.

Dễ thấy: $OK$ là đường trun trực của AD.

Ta có:

$\angle KDM =\angle KIA =\angle KAI \Rightarrow KIMD $ nội tiếp. $\Rightarrow  \angle DAM + \angle AMK =90 \Rightarrow  \angle BIJ +\angle IBC =90.$

$\Rightarrow  KI \perp BC.$

các cách giải trên cũng khá hay, mình xin làm thêm 1 mở rộng nữa cho bài 40

Bài 42:cho tứ giác ABCD nội tiếp có giao điểm $I$ của 2 đường chéo, $P$ và $Q$ lần lượt là trung điểm của $AB$ và $CD$, $K$,$I$,$J$, $L$ lần lượt là tâm của $(IAD)$ , $(IBC)$, $(IBA)$, $(ICD)$. Chứng minh rằng $JI\parallel LK$

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 06-04-2017 - 17:55

[duonghaibang]

Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O) với trực tâm H. BH,CH cắt (O) lần lượt tại E,F khác B,C. M,N lần lượt thuộc đoạn AB, AC sao cho M,H,N thẳng hàng,
1, Chứng minh rằng $\angle AFM = \angle AHM$
2, Chứng minh FM cắt EN tại P nằm trên (O)
3, Giả sử AP là phân giác $\angle BAC$ . CHứng minh MN vuông góc với AP

[Nguyenphuctang]

Bài 42: (Đề vòng 2 KHTN 2015-2016)

Cho $\bigtriangleup ABC$ nhọn không cân với $AB < AC$. $M$ là trung điểm của $BC$. $H$ là hình chiếu vuông góc của $B$ lên $AM$. Trên tia đối $AM$ lấy $N$ sao cho $AN=2MH$. 

a/ Chứng minh rằng: $BN = AC$.

b/ Gọi $Q$ là điểm đối xứng với $A$ qua $N$. $AC\cap BQ=D$. Chứng minh rằng $B;D;N;C$ cùng thuộc một đường tròn $(O)$.

c/ $(AQD) \cap(O)=G$($G$ khác $D$). Chứng minh rằng $NG \parallel BC$.

Phiền bạn duonghaibang ghi nguồn và đánh số cho bài trên theo đúng quy định của Topic nhé!

[Mr Cooper]

$\boxed{43}$ Cho tam giác $ABC$ nhọn nội tiếp $(O)$ các đường cao $BE,CF,AD$ cắt nhau tại $H$, lấy $H$' đối xứng với $H$ qua $BC$, $H'E$ cắt $(O)$ tại $M$. Chứng minh $BM$ đi qua trung điểm $EF$.

[NTMFlashNo1]

$\boxed{43}$ Cho tam giác $ABC$ nhọn nội tiếp $(O)$ các đường cao $BE,CF,AD$ cắt nhau tại $H$, lấy $H$' đối xứng với $H$ qua $BC$, $H'E$ cắt $(O)$ tại $M$. Chứng minh $BM$ đi qua trung điểm $EF$.

Hình học VMF.png

Dễ thấy $D$ là trung điểm của $HH'$

$H$ là tâm nội tiếp tam giác $DEF$

$ABDE$ nội tiếp nên $\widehat{FBE}=\widehat{HDE}$

$\Rightarrow \triangle EFB\sim \triangle EHD(g.g)$

$K$ là trung điểm $EF$

$\Rightarrow \frac{EF}{HE}=\frac{BF}{HD}$ hay $\frac{EF}{2HE}=\frac{BF}{2HD}$

$\Rightarrow \frac{FK}{HE}=\frac{BF}{HH'}$

$\Rightarrow \triangle KFB\sim \triangle EHH' (c.g.c)$

$\Rightarrow \widehat{FBK}=\widehat{HH'E}=\widehat{ABM}$

$\Rightarrow Q.E.D$

 

 

 

 

Tham khảo tại đây