Lời giải bài toán.
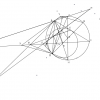
Bổ đề 1. Cho tam giác $ABC$ nội tiếp $(O)$ có tâm nội tiếp $I,L,K$ lần lượt là đối xứng của $C,B$ qua $IB,IC.$ Khi đó $KL \perp OI.$
Chứng minh. $(I)$ tiếp xúc với $BC,CA,AB$ tại $U,V,G.$
Đặt $(a,b,c)=(AG,BG,UC).$ Vì $BL=BC,BG=BU$ nên $GL=UC=c.$
Ta có: $LO^{2}-LI^{2}=LA.LB+R^{2}-(GL^{2}+r^{2})=(LA-GA).LB-GL^{2}+R^{2}-r^{2}=(c-a)(b+c)-c^{2}+(R^{2}-r^{2})=bc-a(b+c)+(R^{2}-r^{2}).$
Tương tự: $KO^{2}-KI^{2}=bc-a(b+c)+(R^{2}-r^{2})$ nên $LO^{2}-LI^{2}=KO^{2}-KI^{2}.$
Theo định lí Carnot, $LK \perp OI.$
Bổ đề 2. Gọi $P,Q$ là tâm đường tròn bàng tiếp $C,B$. Khi đó $PL,QK$ cắt nhau tại điểm nằm trên $OI.$
Chứng minh. $PL$ cắt $(ABI)$ tại $E,KQ$ cắt $(AIC)$ tại $F.LK\cap IO$ tại $T.$ Theo bổ đề 1 thì $\widehat{LTI}=90^0.$
Mặt khác ta có $\widehat{LEI}=\widehat{LTI}=90^0 \Rightarrow LEIT$ nội tiếp. (1)
Tương tự $\widehat{KFI}=\widehat{KTI}=90$ $\Rightarrow FKIT$ nội tiếp. (2)
Ta có $(FL,FK)=(IL,IQ)=(IQ,IC)=(IB,IP)=(IP,IK)=(EL,EK)\Rightarrow ELFK$ nội tiếp. (3)
(1)(2)(3) $\Rightarrow EL,FK,IT$ đồng quy, đpcm.
Trở lại bài toán ban đầu.
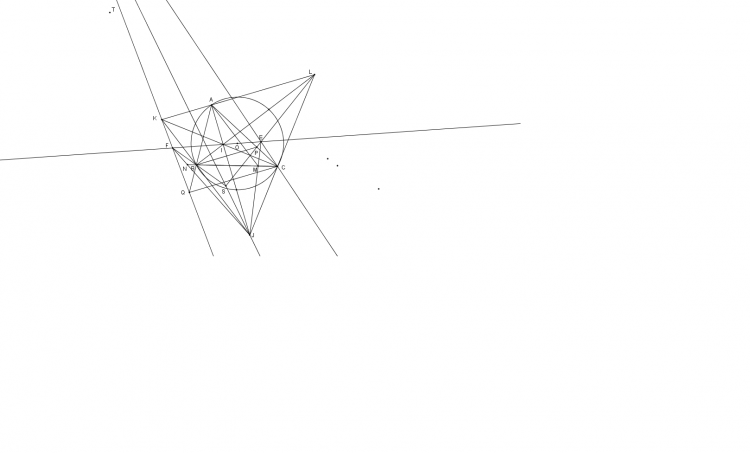
Gọi $K,L$ lần lượt là tâm bàng tiếp góc $C,B.$ Theo bổ đề 2 $JM,LP,OI$ đồng quy suy ra $P,E,L$ thẳng hàng. Tương tự $K,F,Q$ thẳng hàng.
Áp dụng định lí Desargues cho 2 tam giác $KFB$ và $ELC \Rightarrow \overline{S,J,T }.$
Bài viết đã được chỉnh sửa nội dung bởi halloffame: 27-02-2017 - 23:26