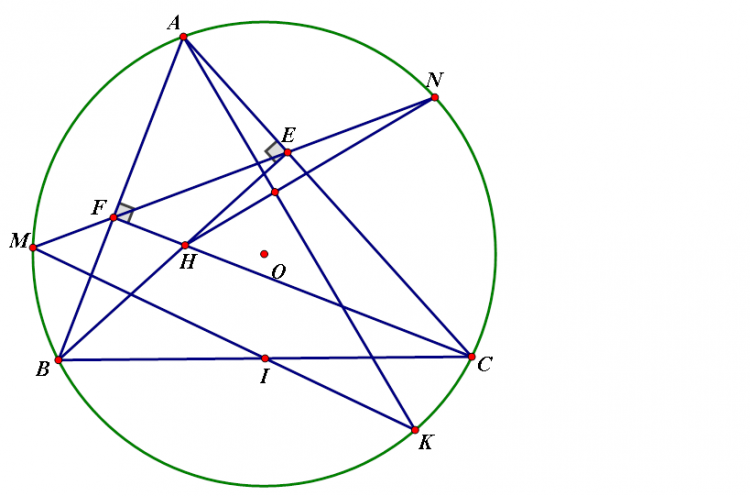
Bài này thì cũng dễ thôi 
Gọi D giao điểm của AH vs BC
đầu tiên ta nhận thấy ÁO vuông góc vs EF (tự cm) suy ra OA vuông góc vs MN suy ra A là điểm chính giữa cung MN
suy ra góc ANM = góc ACN suy ra tam AEN đồng dạng vs tam giác ANC (g.g) suy ra AN2 = AE.AC = AH.AD suy ra tam giác AHN đồng dạng vs tam giác AND (c.g.c)
suy ra góc ANH = góc ADN
để chứng minh AK vuông góc vs HN ta cần chứng minh góc ANH + góc KAN = 90 độ tương đương vs cần chứng minh góc ANH + góc KMN = 90 độ
mà ta có góc ADN + góc NDC = 90 độ suy ra ta cần chứng minh góc NDC = góc NMK hay chứng minh tứ giác MNID nội tiếp
*chứng minh tứ giác MNID nội tiếp,
Kéo dài MN cắt BC tại P ta có PM.PN = PB.PC (tứ giác MNCB nội tiếp) ta cần chứng minh PM.PN = PD.PI tương đương vs cần chứng minh PB.PC = PD.PI
các bạn chứng minh PH vuông góc vs AI(cái này dễ ) suy ra H là trưc tâm của tam giác AIP gọi T là giao điểm của IH và AP suy ra IT vuông góc vs AP mà khi gọi Q là giao điểm của IH và (O) thì IQ vuông góc vs AQ suy ra T trùng Q suy ra T nằm trên (O) suy ra PT.PA = PM.PN mà PT.PA = PD.PI suy ra PM.PN = PD.PI suy ra tam giác PMD đồng dạng vs tam giác PIN từ đó suy ra tứ giác MDIN nội tiếp
kết hợp vs trên ta chứng minh được bài toán
Bài viết đã được chỉnh sửa nội dung bởi BK29DTM: 11-03-2017 - 10:14