Đề thi HSG tỉnh Thanh Hóa năm 2016-2017

Đề thi HSG tỉnh Thanh Hóa năm 2016-2017
#1
 Đã gửi 11-03-2017 - 21:30
Đã gửi 11-03-2017 - 21:30

#2
 Đã gửi 11-03-2017 - 22:18
Đã gửi 11-03-2017 - 22:18

bài 2
với x ; y # 0
hệ ptr tương đương
$\left\{\begin{matrix} 1+\frac{1}{x+y}=\frac{3}{2\sqrt{x}} & \\ & \end{matrix}1-\tfrac{1}{x-y}=\frac{1}{2\sqrt{y}}\right.$
sau đó cộng và trừ 2 phương trình cho nhau
được 2 phương trình mới thì nhân lại với nhau sẽ tạo về ptr tích thế là ok
- trambau và IrisMorgenster thích
Lê Đình Văn LHP ![]()
![]()
![]()
#4
 Đã gửi 12-03-2017 - 09:49
Đã gửi 12-03-2017 - 09:49

SỞ GIÁO DỤC VÀ ĐÀO TẠO KÌ THI HỌC SINH GIỎI CẤP TỈNH
THANH HÓA NĂM HỌC 2016-2017
Ngày thi: 11/3/2017. Thời gian:150 phút
Câu 1: (4,0 điểm)
1. Cho biểu thức $P=(1+\frac{4}{\sqrt{x}-1}+\frac{1}{x-1}) : (\frac{x+2\sqrt{x}}{x-1})$ với $x>0;x\neq1$. Rút gọn biểu thức $P$
2. Cho biểu thức $F(x)=\sqrt{x^{8}+12x+12}-3x$. Gọi $x_{0}$ là 1 nghiệm của phương trình $x^{2}-x-1=0$. Tính giá trị của $F(x_{0})$
Câu 2: (4,0 điểm)
1. Cho phương trình $mx^{2}+x+m-1=0$. Xác định m để phương trình có 2 nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn $\left | \frac{1}{x_{1}}-\frac{1}{x_{2}} \right |>1$.
2. Giải hệ phương trình $\begin{cases} & 2\sqrt{x}\left ( 1+\frac{1}{x+y} \right )=3 \\ & 2\sqrt{y}\left ( 1-\frac{1}{x+y} \right )=1 \end{cases}$.
Câu 3: (4,0 điểm)
1.Tìm nghiệm nguyên của phương trình $x^{2}(y-5)-xy=x-y+1$.
2.Tìm các số tự nhiên $x, y, z$ đồng thời thỏa mãn hai điều kiện sau: $x^{3}+y^{3}=2z^{3}$ và $x+y+z$ là số nguyên tố.
Câu 4: (6,0 điểm)
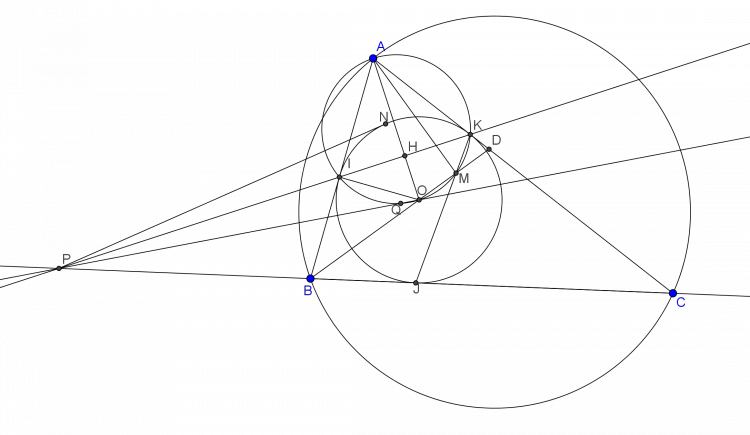
Cho $\widehat{ABx}$ cố định, trên tia $Bx$ lấy điểm $C$ sao cho $AB<AC, AB<BC$. Đường tròn tâm $O$ nội tiếp tam giác $ABC$ tiếp xúc với các cạnh $AB, BC, AC$ lần lượt tại $I, J, K$ . Tia $BO$ cắt các đường thẳng $JK$ , $AC$ lần lượt tại $M$ và $D$ .
1. Chứng minh rằng$\widehat{AOB}=90^{\circ} +\frac{1}{2}\widehat{ACB}$ và năm điểm $A, I, O, M, K$ cùng nằm trên 1 đường tròn.
2. Chứng minh $DK.BM=DM.BJ$ và đường thẳng $JK$ luôn đi qua 1 điểm cố định khi điểm $C$ di động trên tia $Bx$ thỏa mãn giả thiết.
3. Gọi $P$ là giao điểm của đường thẳng $KI$ và đường thẳng $BC$, đường thẳng $AJ$ cắt đường tròn $(O)$ tại điểm thứ hai là $N$. Chứng minh rằng $PN$ là tiếp tuyến của đường tròn $(O)$.
Câu 5: (2,0 điểm)
Cho $a, b, c$ là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức
$P=\frac{(a+b+c)^{2}}{30(a^{2}+b^{2}+c^{2})}+\frac{a^{3}+b^{3}+c^{3}}{4abc}-\frac{131(a^{2}+b^{2}+c^{2})}{60(ab+bc+ca)}.$
---------Hết--------
P/s: lần đầu đánh đề có gì sai mong mọi người bỏ qua
Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 12-03-2017 - 11:44
- namcpnh, PlanBbyFESN, linhtrang1602 và 3 người khác yêu thích
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
----- Michelangelo----
#5
 Đã gửi 12-03-2017 - 20:24
Đã gửi 12-03-2017 - 20:24

Câu 5: (2,0 điểm)
Cho $a, b, c$ là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức
$P=\frac{(a+b+c)^{2}}{30(a^{2}+b^{2}+c^{2})}+\frac{a^{3}+b^{3}+c^{3}}{4abc}-\frac{131(a^{2}+b^{2}+c^{2})}{60(ab+bc+ca)}.$
Ta có:$\frac{a^{3}+b^3+c^3}{4abc}-\frac{3}{4}=\frac{(a+b+c)(a^2+b^2+c^2-ab-bc-ac)}{4abc}
\geq \frac{(a+b+c)(a^2+b^2+c^2-ab-bc-ac)}{\frac{4}{9}(a+b+c)(ab+bc+ac)}
=\frac{9(a^2+b^2+c^2-ab-bc-ac)}{4(ab+bc+ac)}$
Đặt $x=a^2+b^2+c^2;y=ab+bc+ac$
Ta có:$\geq \frac{x+2y}{30x}+\frac{9(x-y)}{4y}-\frac{131x}{60y}+3/4
$=\frac{1}{30}+\frac{y}{15x}+\frac{9x}{4y}-\frac{9}{4}-\frac{131x}{60y}$+3/4
$=\frac{x}{15y}+\frac{y}{15x}-\frac{22}{15}$
$\geq \frac{2}{15}-\frac{22}{15}=\frac{-4}{3}$
Đẳng thức xảy ra$\Leftrightarrow a=b=c$
- VOHUNGTUAN, NMD202 và NHoang1608 thích
#6
 Đã gửi 12-03-2017 - 20:25
Đã gửi 12-03-2017 - 20:25

bài 2
với x ; y # 0
hệ ptr tương đương
$\left\{\begin{matrix} 1+\frac{1}{x+y}=\frac{3}{2\sqrt{x}} & \\ & \end{matrix}1-\tfrac{1}{x-y}=\frac{1}{2\sqrt{y}}\right.$
sau đó cộng và trừ 2 phương trình cho nhau
được 2 phương trình mới thì nhân lại với nhau sẽ tạo về ptr tích thế là ok
Cụ thể hơn được ko
#7
 Đã gửi 12-03-2017 - 21:02
Đã gửi 12-03-2017 - 21:02

Với$x=0\Rightarrow y^3=2z^3\Rightarrow y=z=0\Rightarrow x+y+z=0$không phải số nguyên tố(Loại)
Tương tự ta cũng loại với y=0
Nên$x;y\geq 1\Rightarrow z\geq 1$
Đặt p=x+y+z là số nguyên tố
Ta có:$x^3+y^3=2z^3$
$\Leftrightarrow (p-z)(x^2+y^2-xy)=2z^3$
Mà$(p-z,z^3)=1$$\Rightarrow x^2+y^2-xy= z^{3}k(k\epsilon \mathbb{N}*)$
$\Rightarrow (x+y)k=2$
$x=y=k=1$
$\Rightarrow z=1\Rightarrow p=3$(Thỏa mãn)
Vậy(x;y;z)=(1;1;1)
#8
 Đã gửi 12-03-2017 - 22:50
Đã gửi 12-03-2017 - 22:50

Câu 3: (4,0 điểm)
1.Tìm nghiệm nguyên của phương trình $x^{2}(y-5)-xy=x-y+1$.
Ta có: $x^{2}(y-5)-xy=x-y+1\Leftrightarrow x^{2}(y-5)-x(y+1)+y-1=0$
$\Delta =(y+1)^2-4(y-1)(y-5)=-3y^2+26y-19 \geq 0\Leftrightarrow \frac{13-4\sqrt{7}}{3}\leq y \leq \frac{13+4\sqrt{7}}{3}$
y nguyên...
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 12-03-2017 - 22:52
- HoangTienDung1999 và ToanTHPTHT thích
#9
 Đã gửi 13-03-2017 - 13:18
Đã gửi 13-03-2017 - 13:18

#10
 Đã gửi 16-03-2017 - 20:36
Đã gửi 16-03-2017 - 20:36

Lời giải của thầy Nguyễn Việt Hùng - Giáo viên trường THPT Chuyên KHTN-ĐHQGHN.


#11
 Đã gửi 02-04-2017 - 18:03
Đã gửi 02-04-2017 - 18:03

![]()
![]()
![]() Đề năm nay nhẹ hơn đề năm ngoái chút chút :
Đề năm nay nhẹ hơn đề năm ngoái chút chút :
[Dương Tuệ Linh ]
[Linh]
#12
 Đã gửi 05-05-2017 - 11:04
Đã gửi 05-05-2017 - 11:04

Giải bài hình câu cuối sai rồi bạn nhé: O, Q, P chưa thẳng hàng
#13
 Đã gửi 05-05-2017 - 17:03
Đã gửi 05-05-2017 - 17:03

Ta có:$\frac{a^{3}+b^3+c^3}{4abc}-\frac{3}{4}=\frac{(a+b+c)(a^2+b^2+c^2-ab-bc-ac)}{4abc}
\geq \frac{(a+b+c)(a^2+b^2+c^2-ab-bc-ac)}{\frac{4}{9}(a+b+c)(ab+bc+ac)}
=\frac{9(a^2+b^2+c^2-ab-bc-ac)}{4(ab+bc+ac)}$
Đặt $x=a^2+b^2+c^2;y=ab+bc+ac$
Ta có:$\geq \frac{x+2y}{30x}+\frac{9(x-y)}{4y}-\frac{131x}{60y}+3/4
$=\frac{1}{30}+\frac{y}{15x}+\frac{9x}{4y}-\frac{9}{4}-\frac{131x}{60y}$+3/4
$=\frac{x}{15y}+\frac{y}{15x}-\frac{22}{15}$
$\geq \frac{2}{15}-\frac{22}{15}=\frac{-4}{3}$
Đẳng thức xảy ra$\Leftrightarrow a=b=c$
Ta có:
\[\frac{{{{\left( {a + b + c} \right)}^2}}}{{30\left( {{a^2} + {b^2} + {c^2}} \right)}} + \frac{{{a^3} + {b^3} + {c^3}}}{{4abc}} - \frac{{131\left( {{a^2} + {b^2} + {c^2}} \right)}}{{60\left( {ab + bc + ca} \right)}} = \sum\limits_{cyc} {{{\left( {a - b} \right)}^4}\left( {\frac{{a + b + 3c}}{{540abc\left( {{a^2} + {b^2} + {c^2}} \right)}} + \frac{{131}}{{1080ab\left( {ab + bc + ca} \right)}}} \right)} - \frac{4}{3} \ge - \frac{4}{3}\]
Vậy min=-4/3
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#14
 Đã gửi 09-05-2017 - 21:08
Đã gửi 09-05-2017 - 21:08

Các bạn thử giải lại bài hình câu cuối đi
#15
 Đã gửi 10-05-2017 - 11:11
Đã gửi 10-05-2017 - 11:11

Giải bài hình câu cuối sai rồi bạn nhé: O, Q, P chưa thẳng hàng
Các bạn thử giải lại bài hình câu cuối đi
Không cần thẳng hàng đâu. Mình xin trình bày lại để bạn rõ
Gọi $Q$ là giao điểm của $(AIOK)$ và $OP$; $H$ là giao điểm của $OA$ và $IP$ $\Rightarrow \widehat{AQO}=90^o$. Mà $\widehat{OHP}=90^o\Rightarrow AHQP$ nội tiếp $\Rightarrow OQ.OP=OH.OA=OI^2=ON^2\Rightarrow \frac{OQ}{ON}=\frac{ON}{OP}\Rightarrow \Delta ONQ \sim \Delta OPN(g.g)\Rightarrow \widehat{PNO}=\widehat{NQO}=90^o\Rightarrow Q.E.D$
#16
 Đã gửi 12-05-2017 - 22:03
Đã gửi 12-05-2017 - 22:03

Ta có: $x^{2}(y-5)-xy=x-y+1\Leftrightarrow x^{2}(y-5)-x(y+1)+y-1=0$
$\Delta =(y+1)^2-4(y-1)(y-5)=-3y^2+26y-19 \geq 0\Leftrightarrow \frac{13-4\sqrt{7}}{3}\leq y \leq \frac{13+4\sqrt{7}}{3}$
y nguyên...
Bạn chưa xét TH hệ số a=0
TH1: y-5=0
TH2: $y-5\neq 0$
Bài viết đã được chỉnh sửa nội dung bởi THAN DONG TOAN HOC LDK: 12-05-2017 - 22:50
#17
 Đã gửi 12-05-2017 - 22:23
Đã gửi 12-05-2017 - 22:23

Đề này mình làm hôm đó được 15 điểm thôi, nhưng cũng cao nhất Tp Thanh Hóa
#18
 Đã gửi 12-05-2017 - 22:41
Đã gửi 12-05-2017 - 22:41

Giải bài hình câu cuối sai rồi bạn nhé: O, Q, P chưa thẳng hàng
Câu 2.1 bạn giải thiếu rồi
Kết quả phải là
$$0\leq m\leq \frac{6}{5}, m\neq 1$$
Không tin bạn làm lại xem
Bài viết đã được chỉnh sửa nội dung bởi THAN DONG TOAN HOC LDK: 12-05-2017 - 22:53
#19
 Đã gửi 13-05-2017 - 17:13
Đã gửi 13-05-2017 - 17:13

câu hình b hình như sai rồi, C di động thì BD di động nên M di động
#20
 Đã gửi 17-05-2017 - 10:37
Đã gửi 17-05-2017 - 10:37

Không cần thẳng hàng đâu. Mình xin trình bày lại để bạn rõ
Gọi $Q$ là giao điểm của $(AIOK)$ và $OP$; $H$ là giao điểm của $OA$ và $IP$ $\Rightarrow \widehat{AQO}=90^o$. Mà $\widehat{OHP}=90^o\Rightarrow AHQP$ nội tiếp $\Rightarrow OQ.OP=OH.OA=OI^2=ON^2\Rightarrow \frac{OQ}{ON}=\frac{ON}{OP}\Rightarrow \Delta ONQ \sim \Delta OPN(g.g)\Rightarrow \widehat{PNO}=\widehat{NQO}=90^o\Rightarrow Q.E.D$
Theo cach nay thì góc NQO chưa chắc bằng 90 độ
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh