Chủ đề này có 15 trả lời

[Hoang Dinh Nhat]

Lúc sáng mới đi thi về.

Hình gửi kèm

• 

[HoangKhanh2002]

SỞ GIÁO DỤC VÀ ĐÀO TẠO            KÌ THI HỌC SINH GIỎI VĂN HOÁ LỚP 9

            QUẢNG TRỊ                                    Khoá thi ngày 15 tháng 3 năm 2017

      ĐỀ THI CHÍNH THỨC                                         Môn thi: TOÁN

     (Đề thi gồm có 01 trang)           Thời gian làm bài: 150 phút (không kể thời gian giao đề)

 

Bài 1: (5,0 điểm) Cho biểu thức $A=\frac{x\sqrt{x}}{x\sqrt{x}+1}:\frac{\sqrt{x}-1}{x(\sqrt{x}-1)+\sqrt{x}}$

1. Tìm điều kiên của x để A có nghĩa và rút gọn A

2. Tính giá trị của A khi $x=\sqrt[3]{\frac{3+2\sqrt{2}}{3-2\sqrt{2}}}-\sqrt[3]{\frac{3-2\sqrt{2}}{3+2\sqrt{2}}}$

3. Giả sử số thực x thoả mãn $x\geq 5$. Tìm giá trị nhỏ nhất của A

 

Bài 2 (5,0 điểm)

1. Giải phương trình $x+11=7\sqrt{x+1}$

2. Cho các số thực dương a, b, c, d. Chứng minh rằng: $\frac{b}{(a+\sqrt{b})^2}+\frac{d}{(c+\sqrt{d})^2}\geq \frac{\sqrt{bd}}{ac+\sqrt{bd}}$

 

Bài 3 (2,0 điểm) Giải hệ phương trình: $\left\{\begin{matrix} xy+x+y=x^2-2y^2\\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{matrix}\right.$

 

Bài 4 (6,0 điểm)

1. Cho tứ giác ABCD nội tiếp đường tròn (O), đường kính AD. Hai đường chéo AC và BD cắt nhau tại E; Gọi F là hình chiếu của E trên AD và G là trung điểm ED. Đường tròn ngoại tiếp tam giác DGF cắt (O) tại điểm thứ hai là H ($H\not\equiv D$). Gọi I là giao điểm của BC và FG

a) Chứng minh rằng tứ giác BCGF nội tiếp đường tròn

b) Chứng minh rằng D, I, H thẳng hàng

2. Bên trong hình tròn có bán kính bằng 1 chọn 7 điểm bất kí. Chứng minh rằng tồn tại 2 điểm trong 7 điểm đã cho có khoảng cách giữa chúng nhỏ hơn 1

 

Bài 5 (2,0 điểm)

1. Cho các số thực x, y. Chứng minh rằng: $\left [ x \right ]+\left [ y \right ]\leq \left [ x +y\right ]\leq \left [ x \right ]+\left [ y \right ]+1$ (Kí hiệu $\left [ x \right ]$ là số nguyên lớn nhất không vượt quá x)

2. Ta gọi một bộ số nguyên tố đẹp khi tích của các số nguyên tố này bằng 10 lần tổng của chúng. Hãy tìm tất cả các bộ số nguyên tố đẹp nói trên ( các số trong bộ không nhất thiết phải phân biệt).

--------------------HẾT--------------------

 

Thí sinh không được sử dụng tài liêu. Cán bộ coi thi không giải thích gì thêm

 

 

Họ và tên thí sinh:...................................................................Số báo danh:...................

 

PS: Bạn xem lại đúng chưa vì một số chỗ hơi mờ

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 16-03-2017 - 10:42

[NHoang1608]

Bài 2b): Sử dụng bất đẳng thức quen thuộc $\frac{1}{(x+1)^{2}}+\frac{1}{(y+1)^{2}}\geq \frac{1}{xy+1}$ (có thể chứng minh bằng biến đổi tương đương)

Ta có: $\frac{1}{(\frac{a}{\sqrt{b}}+1)^{2}}+\frac{1}{(\frac{c}{\sqrt{d}}+1)^{2}}\geq \frac{1}{\frac{ac}{\sqrt{bd}}+1}$

          $\Leftrightarrow \frac{b}{(a+\sqrt{b})^{2}}+\frac{d}{(c+\sqrt{d})^{2}}\geq \frac{bd}{ac+\sqrt{bd}}.$ ĐPCM. Dấu bằng xảy ra khi $a=\sqrt{b}, c=\sqrt{d}$

Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 15-03-2017 - 17:16

[Ngoc Hung]

 

Bài 5 (2,0 điểm)

2. Ta gọi một bộ số nguyên tố đẹp khi tích của các số nguyên tố này bằng 10 lần tổng của chúng. Hãy tìm tất cả các bộ số nguyên tố đẹp nói trên ( các số trong bộ không nhất thiết phải phân biệt).

 

Dễ thấy bộ số nguyên tố đẹp phải chứa số 2 và 5. Giả sử $p_{1}\leq p_{2}\leq ...\leq p_{n}$ là các số còn lại trong bộ.

Ta có $10p_{1}...p_{n}=10(7+p_{1}+...+p_{n})\Rightarrow p_{1}...p_{n}=7+p_{1}+...+p_{n}$. 

Ta có $x\geq 2;y\geq 2\Rightarrow xy\geq x+y$. Do đó bằng quy nạp ta chứng minh được $x_{1}...x_{k}\geq x_{1}+...+x_{k}$ với $x_{i}\geq 2$ (i = 1, 2, 3, .., k)

Do đó $p_{1}+...+p_{n}+7=p_{1}...p_{n}\geq (p_{1}+...+p_{n-1})p_{n}\Leftrightarrow s+p_{n}+7\geq sp_{n}$ với $s=p_{1}+...+p_{n-1}$

Suy ra $(p_{n}-1)(s-1)\leq 8$. Do $s\geq 2$ suy ra $p_{n}-1\leq 8\Rightarrow p\in \left \{ 2;3;5;7 \right \}$

Lần lượt xét các TH ta có bộ số (2; 3; 5; 5) và các hoán vị của chúng

[HoangKhanh2002]

Bài 4 (6,0 điểm)

2. Bên trong hình tròn có bán kính bằng 1 chọn 7 điểm bất kí. Chứng minh rằng tồn tại 2 điểm trong 7 điểm đã cho có khoảng cách giữa chúng nhỏ hơn 1

Chia hình tròn thành 6 hình quạt đều

Theo nguyên lí Dirichlet thì có 2 điểm nằm trong 1 hình quạt

+) Nếu 1 trong 2 điểm đó trùng tâm thì luôn đúng

+) Nêu 2 điểm đó không trùng tâm thì giả sử đó là A và B nằm trong hình quạt COD có $\widehat{COD}=60^o$ thì qua A và B kẻ các bán kính: $OA; OB$ cắt (O) tại $A_{1};B_{1}\Rightarrow \widehat{A_{1}OB{1}}\leq 60^o\Rightarrow AB\leq max\left \{ OA;OB \right \}<1$

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 15-03-2017 - 18:09

[Ngoc Hung]

Bài 5 (2,0 điểm)

1. Cho các số thực x, y. Chứng minh rằng: $\left [ x \right ]+\left [ y \right ]\leq \left [ x +y\right ]\leq \left [ x \right ]+\left [ y \right ]+1$ (Kí hiệu $\left [ x \right ]$ là số nguyên lớn nhất không vượt quá x)

 

Ta có $\left [ x \right ]+\left [ y \right ]=\left [ \left [ x \right ] +\left \{ x \right \}+\left [ y \right ]+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \}+\left \{ y \right \} \right ]$

Do $0\leq \left \{ x \right \}< 1\Rightarrow 0\leq \left \{ x \right \}+\left \{ y \right \}< 2\Rightarrow 0\leq \left [ \left \{ x \right \} +\left \{ y \right \}\right ]< 1$

Từ đó suy ra $\left [ x+y \right ]\leq \left [ x \right ]+\left [ y \right ]+1$

Mặt khác ta lại có $x=\left [ x \right ]+\left \{ x \right \};y=\left [ y \right ]+\left \{ y \right \}\Rightarrow \left [ x+y \right ]=\left [ \left [ x \right ] +\left [ y \right ]+\left \{ x \right \}+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \} +\left \{ y \right \}\right ]\geq \left [ x \right ]+\left [ y \right ]$

[lenadal]

câu 5 b 

đặt 3 số nguyên tố là a ; b;c .....$(a\leq b\leq c.....)$

ta có $abc....=10(a+b+c.....)$

suy ra abc... chia hết cho 5 

abc chia hết cho 2

mà a;b;.....c là số ng tố

suy ra a;b;c...... có 1 số bằng 2 một số bằng 5

đến đây ok rồi

Bài viết đã được chỉnh sửa nội dung bởi lenadal: 15-03-2017 - 22:27

[Hoang Dinh Nhat]

Ta có $\left [ x \right ]+\left [ y \right ]=\left [ \left [ x \right ] +\left \{ x \right \}+\left [ y \right ]+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \}+\left \{ y \right \} \right ]$

Do $0\leq \left \{ x \right \}< 1\Rightarrow 0\leq \left \{ x \right \}+\left \{ y \right \}< 2\Rightarrow 0\leq \left [ \left \{ x \right \} +\left \{ y \right \}\right ]< 1$

Từ đó suy ra $\left [ x+y \right ]\leq \left [ x \right ]+\left [ y \right ]+1$

Mặt khác ta lại có $x=\left [ x \right ]+\left \{ x \right \};y=\left [ y \right ]+\left \{ y \right \}\Rightarrow \left [ x+y \right ]=\left [ \left [ x \right ] +\left [ y \right ]+\left \{ x \right \}+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \} +\left \{ y \right \}\right ]\geq \left [ x \right ]+\left [ y \right ]$

 

em không hiểu cho lắm thầy, cái {x} là gì thầy

Bài viết đã được chỉnh sửa nội dung bởi Hoang Dinh Nhat: 16-03-2017 - 08:07

[Hoang Dinh Nhat]

Câu hệ pt như này bạn nè

 

 

Bài 3 (2,0 điểm) Giải hệ phương trình: $\left\{\begin{matrix} xy+x+y=x^2-2y^2\\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{matrix}\right.$

 

 

[HoangKhanh2002]

Câu hệ pt như này bạn nè

Bài 3 (2,0 điểm) Giải hệ phương trình: $\left\{\begin{matrix} xy+x+y=x^2-2y^2\\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{matrix}\right.$

Thế thì dễ:

ĐK: $x\geq 1;y\geq 0$

$\left\{\begin{matrix} xy+x+y=x^2-2y^2\\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x+y)(x-2y-1)=0 \\ x\sqrt{2y}-y\sqrt{x-1}=2x-2y \end{matrix}\right.\Leftrightarrow \Rightarrow \left\{\begin{matrix} x=2y+1\\ (2y+1)\sqrt{2y}-y\sqrt{2y}=2y+2 \end{matrix}\right. \Rightarrow \Rightarrow \left\{\begin{matrix} x=2y+1\\ (y+1)(\sqrt{2y}-2)=0 \end{matrix}\right. \Rightarrow \begin{bmatrix} \left\{\begin{matrix} x=-1\\ y=-1 \end{matrix}\right.(KTM)\\ \left\{\begin{matrix} x=5\\ y=2 \end{matrix}\right.(TM) \end{bmatrix}$

[Ngoc Hung]

em không hiểu cho lắm thầy, cái {x} là gì thầy

 

$\left \{ x \right \}$ là phần lẻ của một số thực. Em xem định nghĩa phần nguyên, phần lẻ

Phần nguyên của số thực x, kí hiệu $\left [ x \right ]$, là số nguyên lớn nhất không vượt quá x, hay $\left [ x \right ]$ là số nguyên thỏa mãn $\left [ x \right ]\leq x< \left [ x \right ]+1$

Phần lẻ của số thực x, kí hiệu $\left \{ x \right \}$ là hiệu $x-\left [ x \right ]$, hay  $\left \{ x \right \}$ là số thực thỏa mãn $0\leq \left \{ x \right \}< 1$  

[Nguyenphuctang]

Bài 4.1:

Câu a:

$\angle BGF=\angle BCF=2\angle ECF$ $\Rightarrow$ tứ giác BCGF nội tiếp. 

Câu b:

Gọi H' là giao điểm của ID với (DFG). Theo hệ thức lượng đường tròn ta có:

ID.IH' = IG.IF. Lại áp dụng 1 lần nữa: IG.IF = IC.IB (Tứ giác BCGF nội tiếp)

$\Rightarrow$ ID.IH' = IC.IB $\Rightarrow$ H' là giao điểm của (O) và (FGD)

$\Rightarrow H\equiv H'$. Vậy I, D, H thẳng hàng.

Câu hình này cứ cho tới cho lui .Đây là đề vào 10 chuyên toán của Trường Đại học Sư Phạm TPHCM 2013 - 2014.

Câu b có thể chuyển thành: Gọi I là giao điểm của HD và BC. Chứng minh rằng: I, G, F thẳng hàng  (Cũng chứng minh tương tự  như trên)

[murasaki]

anh

 

Ta có $\left [ x \right ]+\left [ y \right ]=\left [ \left [ x \right ] +\left \{ x \right \}+\left [ y \right ]+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \}+\left \{ y \right \} \right ]$

Do $0\leq \left \{ x \right \}< 1\Rightarrow 0\leq \left \{ x \right \}+\left \{ y \right \}< 2\Rightarrow 0\leq \left [ \left \{ x \right \} +\left \{ y \right \}\right ]< 1$

Từ đó suy ra $\left [ x+y \right ]\leq \left [ x \right ]+\left [ y \right ]+1$

Mặt khác ta lại có $x=\left [ x \right ]+\left \{ x \right \};y=\left [ y \right ]+\left \{ y \right \}\Rightarrow \left [ x+y \right ]=\left [ \left [ x \right ] +\left [ y \right ]+\left \{ x \right \}+\left \{ y \right \}\right ]=\left [ x \right ]+\left [ y \right ]+\left [ \left \{ x \right \} +\left \{ y \right \}\right ]\geq \left [ x \right ]+\left [ y \right ]$

anh ơi, kí hiệu {x} là sao ạ

[HoangKhanh2002]

anh

 

anh ơi, kí hiệu {x} là sao ạ

Như thầy Hùng đã giải thích ở trên

{x} là phần lẻ của số thực x, {x} = x - [x]; [x] là số nguyên lớn nhất không vượt quá x

[Mr Cooper]

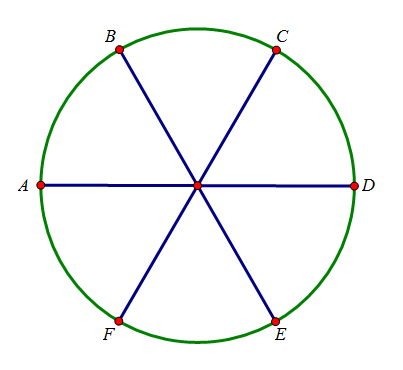
Bài 4. b) Lấy $6$ điểm $A,B,C,D,E,F$ chia đường tròn thành $6$ cung bằng nhau

Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 02-05-2017 - 17:23

[Anhhungbanphim]

Bài 2b): Sử dụng bất đẳng thức quen thuộc $\frac{1}{(x+1)^{2}}+\frac{1}{(y+1)^{2}}\geq \frac{1}{xy+1}$ (có thể chứng minh bằng biến đổi tương đương)
Ta có: $\frac{1}{(\frac{a}{\sqrt{b}}+1)^{2}}+\frac{1}{(\frac{c}{\sqrt{d}}+1)^{2}}\geq \frac{1}{\frac{ac}{\sqrt{bd}}+1}$
          $\Leftrightarrow \frac{b}{(a+\sqrt{b})^{2}}+\frac{d}{(c+\sqrt{d})^{2}}\geq \frac{bd}{ac+\sqrt{bd}}.$ ĐPCM. Dấu bằng xảy ra khi $a=\sqrt{b}, c=\sqrt{d}$

bạn cm bđt áp dụng giúp mk dc ko