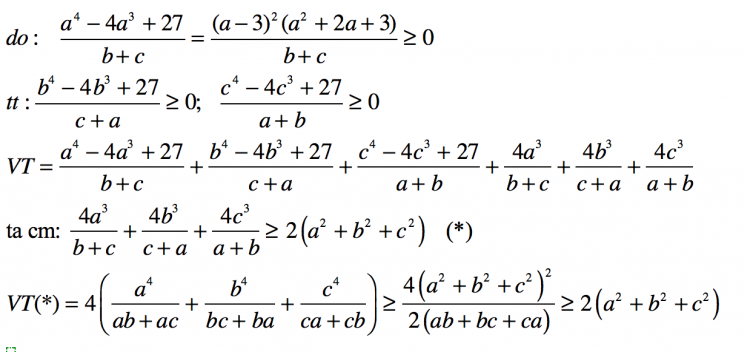Kì thi Olympic tháng 4 TP.HCM lần 3 2016-2017 lớp 10

Kì thi Olympic tháng 4 TP.HCM lần 3 2016-2017 lớp 10
#1
 Đã gửi 08-04-2017 - 18:28
Đã gửi 08-04-2017 - 18:28

#2
 Đã gửi 08-04-2017 - 19:14
Đã gửi 08-04-2017 - 19:14

#3
 Đã gửi 08-04-2017 - 20:19
Đã gửi 08-04-2017 - 20:19

Bài 3 đề chuyên
Áp dụng bđt $AM-GM$ thì ta có: $\frac{a^{4}}{3}+\frac{a^{4}}{3}+\frac{a^{4}}{3}+27 \geq 4\sqrt[4]{a^{12}} = 4a^{3}$
$\Rightarrow a^{4}+27 \geq 4a^{3}$ $(1)$
Sử dụng $(1)$ và áp dụng bđt $AM-GM$ thì ta có:
$\frac{a^{4}+27}{b+c} + a(b+c) \geq \frac{4a^{3}}{b+c} + a(b+c) \geq 2\sqrt{\frac{4a^{3}}{b+c}.a(b+c)} = 4a^{2}$
Suy ra $\frac{a^{4}+27}{b+c} + a(b+c) \geq 4a^{2}$ $(2)$
Hoàn toàn tương tự thì ta có : $ \frac{b^{4}+27}{c+a} + b(c+a) \geq 4b^{2}$ $(3)$
$ \frac{c^{4}+27}{a+b} + c(a+b) \geq 4c^{2}$ $(4)$
Cộng $(2)(3)(4)$ vế theo vế thì ta được $\frac{a^{4}+27}{b+c}+ \frac{b^{4}+27}{c+a} +\frac{c^{4}+27}{a+b} + 2(ab+bc+ca) \geq 4(a^{2}+b^{2}+c^{2})$ $(5)$
Lại có $ab+bc+ca \leq a^{2}+b^{2}+c^{2} \Rightarrow 2(ab+bc+ca) \leq 2(a^{2}+b^{2}+c^{2})$ $(6)$
Từ $(5)$ và $(6)$ suy ra $\frac{a^{4}+27}{b+c}+ \frac{b^{4}+27}{c+a} +\frac{c^{4}+27}{a+b} + 2(a^{2}+b^{2}+c^{2}) \geq 4(a^{2}+b^{2}+c^{2})$
$\Leftrightarrow \frac{a^{4}+27}{b+c}+ \frac{b^{4}+27}{c+a} +\frac{c^{4}+27}{a+b} \geq 2(a^{2}+b^{2}+c^{2})$ $Q.E.D$
Đẳng thức xảy ra khi $a=b=c=3$
Bài viết đã được chỉnh sửa nội dung bởi NHoang1608: 08-04-2017 - 20:34
- ngoisaouocmo và Nghiapnh1002 thích
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
----- Michelangelo----
#4
 Đã gửi 08-04-2017 - 20:21
Đã gửi 08-04-2017 - 20:21

Khối 10 chuyên
Câu bất mình xin làm !!! ![]()
Đặt $a^2+b^2+c^2=x$
Dùng bất đẳng thức Schwarz ta có $\left\{\begin{matrix} \sum \frac{a^4}{b+c}\geq \frac{(a^2+b^2+c^2)^2}{2(a+b+c)}\geq \frac{x^2}{2\sqrt{3x}} & & \\ \sum \frac{27}{b+c}\geq \frac{243}{2(a+b+c)}\geq \frac{243}{2\sqrt{3x}} & & \end{matrix}\right.$
Ta chứng minh $\frac{x^2+243}{2\sqrt{3x}}\geq 2x$
Bình phương hai vế rồi nhân chéo ,,,ta được $\Leftrightarrow (x-27)^2(x^2+6x+81)\geq 0$ ( Đúng )
Vậy ta có đpcm ,,,,dấu bằng xảy ra khi a=b=c=3
- Thanh Long 2001, Trinm, Nghiapnh1002 và 1 người khác yêu thích
SÓNG BẮT ĐẦU TỪ GIÓ
GIÓ BẮT ĐẦU TỪ ĐÂU ?
ANH CŨNG KHÔNG BIẾT NỮA
KHI NÀO...? TA YÊU NHAU .
#5
 Đã gửi 09-04-2017 - 11:43
Đã gửi 09-04-2017 - 11:43

Bài 4 đề chuyên:
Từ đề bài ra ta dễ dàng có $(2n)^2-1=3(2a+1)^2$. Ta cần chứng minh tồn tại số tự nhiên $m$ sao cho $m^2+(m+1)^2=n$, hay $2n-1=(2m+1)^2$. Giả sử $3|2n-1$, khi đó $2n+1\equiv 2 \pmod 3$ và $2n-1=3(2b+1)^2,\ 2n+1=(2c+1)^2$, vô lí. Vậy $3|2n+1$ và $2n-1=(2m+1)^2$, đpcm. $\square$
Bài viết đã được chỉnh sửa nội dung bởi halloffame: 11-04-2017 - 21:24
- lehakhiem212, Nghiapnh1002 và Lolem187 thích
#6
 Đã gửi 09-04-2017 - 14:45
Đã gửi 09-04-2017 - 14:45

Bài toán Hình học không mới và đã từng xuất hiện ở đây:
http://analgeomatica...-2-thang-3.html
Trong thời gian thi hạn chế mà độ khó bài hình học thế này thì thật sự không đẹp lắm. Không khác gì việc lấy bài kiểm tra đội tuyển IMO năm 2015 ra để làm đề thi chính thức năm vừa rồi.
- quanghung86, hoaichung01, IHateMath và 4 người khác yêu thích
#7
 Đã gửi 09-04-2017 - 17:50
Đã gửi 09-04-2017 - 17:50

#9
 Đã gửi 09-04-2017 - 23:11
Đã gửi 09-04-2017 - 23:11

Bài 3: [đề không chuyên] :v
#10
 Đã gửi 09-04-2017 - 23:27
Đã gửi 09-04-2017 - 23:27

Chia hình vuông có cạnh 12x12 thành 36 hình vuông nhỏ cạnh 2x2 thì mỗi hình vuông nhỏ này chứa đúng một hình tròn có bán kính 1 cm. Mặt khác chỉ có 31 lỗ kim châm nên theo nguyên lí Đi-rích-lê tồn tại ít nhất 5 hình vuông nhỏ không chứa lỗ kim châm nào. Do đó ta có đpcm.
#11
 Đã gửi 10-04-2017 - 23:49
Đã gửi 10-04-2017 - 23:49

Khối 10 chuyên
làm câu bất nha :
Áp dụng BĐT Cô-si :
$3*\frac{a^4}{3} +27 \geq 4a^3$
$3*\frac{b^4}{3} +27 \geq 4b^3$
$3*\frac{c^4}{3} +27 \geq 4c^3$
Sử dụng Cauchy - Schwarts :
$\sum \frac{a^4+27}{b+c}\geq 4*\sum \frac{a^4}{ab+ac}\geq 4*\sum \frac{(a^2+b^2+c^2)^2}{2(ab+bc+ca)}\geq 2\sum a^2$ (đpcm).
Bài viết đã được chỉnh sửa nội dung bởi II3amII3i: 10-04-2017 - 23:50
Những điều chúng ta biết chỉ là giọt nước. Những điều chúng ta không biết là cả một đại dương - Isaac Newton
#12
 Đã gửi 14-04-2017 - 22:03
Đã gửi 14-04-2017 - 22:03

Chia hình vuông có cạnh 12x12 thành 36 hình vuông nhỏ cạnh 2x2 thì mỗi hình vuông nhỏ này chứa đúng một hình tròn có bán kính 1 cm. Mặt khác chỉ có 31 lỗ kim châm nên theo nguyên lí Đi-rích-lê tồn tại ít nhất 5 hình vuông nhỏ không chứa lỗ kim châm nào. Do đó ta có đpcm.
Chia hình vuông có cạnh 12x12 thành 36 hình vuông nhỏ cạnh 2x2 thì mỗi hình vuông nhỏ này chứa đúng một hình tròn có bán kính 1 cm. Mặt khác chỉ có 31 lỗ kim châm nên theo nguyên lí Đi-rích-lê tồn tại ít nhất 5 hình vuông nhỏ không chứa lỗ kim châm nào. Do đó ta có đpcm.
bạn ơi hình như có gì đó ko đúng
#13
 Đã gửi 04-05-2017 - 21:32
Đã gửi 04-05-2017 - 21:32

để vậy thì nói làm gì.lỗ kim châm nằm ngay trên cánh thì sao
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: đề thi học sinh giỏi

|
Toán Trung học Cơ sở →
Tài liệu - Đề thi →
Đề thi chọn đội tuyển Amsterdam lần 3Bắt đầu bởi taconghoang, 03-11-2017 |
|

|
|

|
Toán Trung học Cơ sở →
Tài liệu - Đề thi →
ĐỀ THI HỌC SINH GIỎI TOÁN 9 TRƯỜNG THCS NGUYỄN NGHIÊM QUẢNG NGÃI 2017-2018Bắt đầu bởi taconghoang, 02-11-2017 |
|

|
|

|
Toán Trung học Cơ sở →
Tài liệu - Đề thi →
Đề thi học sinh giỏi vòng 2Bắt đầu bởi hoduchieu01, 14-11-2016 |
|

|
|

|
Toán Trung học Cơ sở →
Tài liệu - Đề thi →
Đề thi học giỏi toán quận lớp 9 2015-2016Bắt đầu bởi hoduchieu01, 30-10-2015 |
|

|
|

|
Toán Trung học Phổ thông và Thi Đại học →
Đại số →
Phương trình - hệ phương trình - bất phương trình →
$x^{4}-2x=y^{2}-y$Bắt đầu bởi dhdhn, 28-01-2015 |
|

|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh