cho a,b,c>0. CMR: $\sqrt{a^{2}+b^{2}-\sqrt{3}ab}+\sqrt{b^{2}+c^{2}-bc}\geq \sqrt{a^{2}+c^{2}}$

cho a,b,c>0. CMR: $\sqrt{a^{2}+b^{2}-\sqrt{3}ab}+\sqrt{b^{2}+c^{2}-bc}\geq \sqrt{a^{2}+c^{2}}$
#1
 Đã gửi 16-04-2017 - 20:53
Đã gửi 16-04-2017 - 20:53

#2
 Đã gửi 16-04-2017 - 21:46
Đã gửi 16-04-2017 - 21:46

cho a,b,c>0. CMR: $\sqrt{a^{2}+b^{2}-\sqrt{3}ab}+\sqrt{b^{2}+c^{2}-bc}\geq \sqrt{a^{2}+c^{2}}$
Ta có định lí hàm Cos trong tam giác: $a=\sqrt{b^2+c^2-2bc.CosA}$
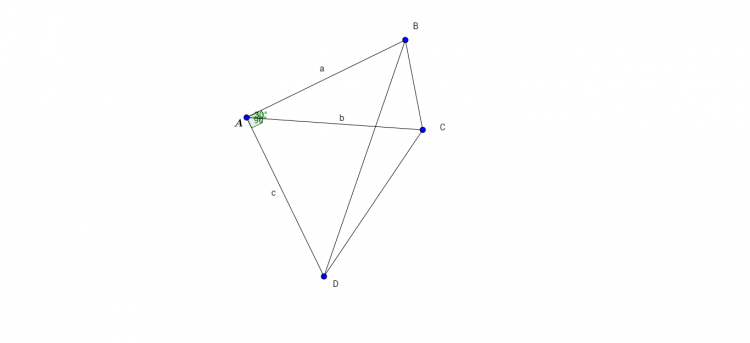
Xét tứ giác ABCD có $\widehat{BAC}=30^{\circ}; \widehat{CAD}=60^{\circ}; AB=a; AC=b, AD=c$
$\Rightarrow \left\{\begin{matrix} BC=\sqrt{a^2+b^2-2ab.Cos30^{\circ}} & & \\ CD=\sqrt{b^2+c^2-2bc.Cos60^{\circ}}& & \\ BD=\sqrt{a^2+c^2} & & \end{matrix}\right.$
$\Leftrightarrow \left\{\begin{matrix} BC=\sqrt{a^2+b^2-\sqrt{3}ab} & & \\ CD=\sqrt{b^2+c^2-bc} & & \\ BD=\sqrt{a^2+c^2} & & \end{matrix}\right.$
Mà $BC+CD\geq BD$
$\Rightarrow \sqrt{a^{2}+b^{2}-\sqrt{3}ab}+\sqrt{b^{2}+c^{2}-bc}\geq \sqrt{a^{2}+c^{2}}$( đpcm)
Dấu ''='' xảy ra $\Leftrightarrow$ C nằm giữa B và D
Bài viết đã được chỉnh sửa nội dung bởi githenhi512: 16-04-2017 - 21:47
- nguyenduy287, viet9a14124869 và lanh24042002 thích
'' Ai cũng là thiên tài. Nhưng nếu bạn đánh giá một con cá qua khả năng trèo cây của nó, nó sẽ sống cả đời mà tin rằng mình thực sự thấp kém''.
Albert Einstein
#3
 Đã gửi 16-04-2017 - 22:03
Đã gửi 16-04-2017 - 22:03

\[VT = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}a - b} \right)}^2} + \frac{1}{4}{a^2}} + \sqrt {{{\left( {b - \frac{c}{2}} \right)}^2} + \frac{3}{4}{c^2}} \ge \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}a - \frac{c}{2}} \right)}^2} + {{\left( {\frac{a}{2} + \frac{{\sqrt 3 }}{2}c} \right)}^2}} = \sqrt {{a^2} + {c^2}} \]
- lanh24042002 yêu thích
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#4
 Đã gửi 16-04-2017 - 22:11
Đã gửi 16-04-2017 - 22:11

bạn trình bày rõ hơn đc ko, cái bước $\geq$ mk ko hiểu
\[VT = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}a - b} \right)}^2} + \frac{1}{4}{a^2}} + \sqrt {{{\left( {b - \frac{c}{2}} \right)}^2} + \frac{3}{4}{c^2}} \ge \sqrt {{{\left( {\frac{{\sqrt 3 }}{2}a - \frac{c}{2}} \right)}^2} + {{\left( {\frac{a}{2} + \frac{{\sqrt 3 }}{2}c} \right)}^2}} = \sqrt {{a^2} + {c^2}} \]
#5
 Đã gửi 16-04-2017 - 22:28
Đã gửi 16-04-2017 - 22:28

bạn trình bày rõ hơn đc ko, cái bước $\geq$ mk ko hiểu
bc do la` su dung BDT Mincopxki
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: bdt

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
$Cho a,b,c\geq 0 \sum a\doteq 1 \sum \sqrt{\frac{a}{2a^{2}+bc}}\geq 2$Bắt đầu bởi TARGET, 07-03-2022 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
$\sqrt{\frac{4x^2+y^2}{2}}+\sqrt{\frac{4x^2+2xy+y^2}{3}}\geq 2x+y$Bắt đầu bởi lmtrtan123334, 18-10-2021 |
|

|
|

|
Toán Trung học Phổ thông và Thi Đại học →
Bất đẳng thức và cực trị →
Tìm GTNN của $P=8(a^2+b^2)-2a-2b$ biết $2a\sin^2 x+b(\sin x-\cos x)^2=0$ luôn có nghiệmBắt đầu bởi hieulu, 02-09-2021 |
|

|
|
 
|
Toán Trung học Phổ thông và Thi Đại học →
Bất đẳng thức và cực trị →
Bất đẳng thứcBắt đầu bởi yungazier, 12-08-2021 |
|

|
|

|
Toán Trung học Phổ thông và Thi Đại học →
Bất đẳng thức và cực trị →
CMR $ 3\sum \frac{b}{a+b+1} \geq \sum \frac{4-a}{a+2} $Bắt đầu bởi Sin99, 24-07-2019 |
|

|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh