Lời giải bài 2 của em ạ
Gọi $X_a,X_b,X_c$ là các đỉnh tam giác đều dựng ra bên ngoài $\triangle ABC$. $Y_a,Y_b,Y_c$ là các đỉnh tam giác đều dựng ra bên trong $\triangle ABC$
Gọi $U_a,V_a$ là các đỉnh tam giác đều dựng vào phía trong $\triangle F_1BC$. Tương tự ta có $U_b,U_c,V_b,V_c$
Do $F_a$ là điểm Fermat thứ hai của $\triangle F_1BC$ nên $F_1BF_aU_a, F_1CV_aF_a$ nội tiếp
Chứng minh tương tự ta có các tứ giác nội tiếp $F_bV_bCF_1,AF_bU_bF_1,AV_cF_cF_1,F_1U_cF_cB$
Do $\angle AF_1V_b = \angle V_bCF_1 = 60^{\circ}$ nên $AF_1$ tiếp xúc $F_bV_bCF_1$. Từ đây suy ra $AF_b.AV_b = AF_1^2$
Tương tự ta có $AF_1^2 = AU_c.AF_c$ nên tứ giác $F_cU_cF_bV_b$ nội tiếp. Tương tự ta cũng có các tứ giác nội tiếp $F_bU_bU_aF_a,V_aF_aF_cV_c$
Ta có $\angle BF_2C = \angle BY_aC = BU_cC = \angle BV_bC = 180^{\circ} - \angle BF_aC = 60^{\circ}$ nên các điểm $U_c,F_2,Y_a,V_b,C,F_a,B$ đồng viên
Tương tự ta có $A,F_b,C,V_a,Y_b,V_c,F_2$ đồng viên
Từ đây ta có biến đổi góc $\angle F_2F_bF_c = \angle AF_bF_c - \angle AF_bF_2 = \angle AU_cV_b - \angle AF_bF_2 $
Và $\angle F_2F_aF_c = \angle F_2F_aB - \angle F_cF_aB = \angle F_2F_aB - \angle BV_cV_a= \angle F_2CB - \angle BV_cV_a$
Ta cần chứng minh $\angle F_2F_aF_c = \angle F_2F_bF_c$. Điều này tương đương với $\angle AU_cV_b+ \angle BV_cV_a = \angle ACB $
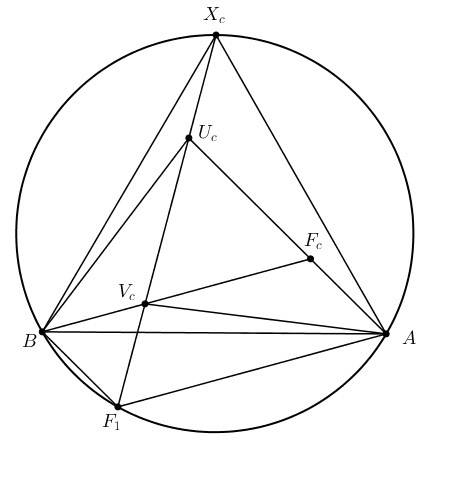
Khi và chỉ khi $\angle AU_cF_1 +\angle BV_cF_1 = \angle F_1BC+\angle F_1AC+\angle BAC = 120^{\circ}$
Điều này tương đương với $\angle U_cBV_c = \angle U_cAV_c$
Thật vậy ta có do $BF_cAF_1$ là hình bình hành nên $F_cA = BF_1 = BV_c$
Mà $V_cU_c = V_cF_c$ suy ra $\triangle U_cV_cB = \triangle V_cF_cA \implies \angle U_cBV_c = \angle U_cAV_c$. Vậy ta có điều cần chứng minh là đúng
Vậy $F_a,F_b,F_c,F_2$ đồng viên
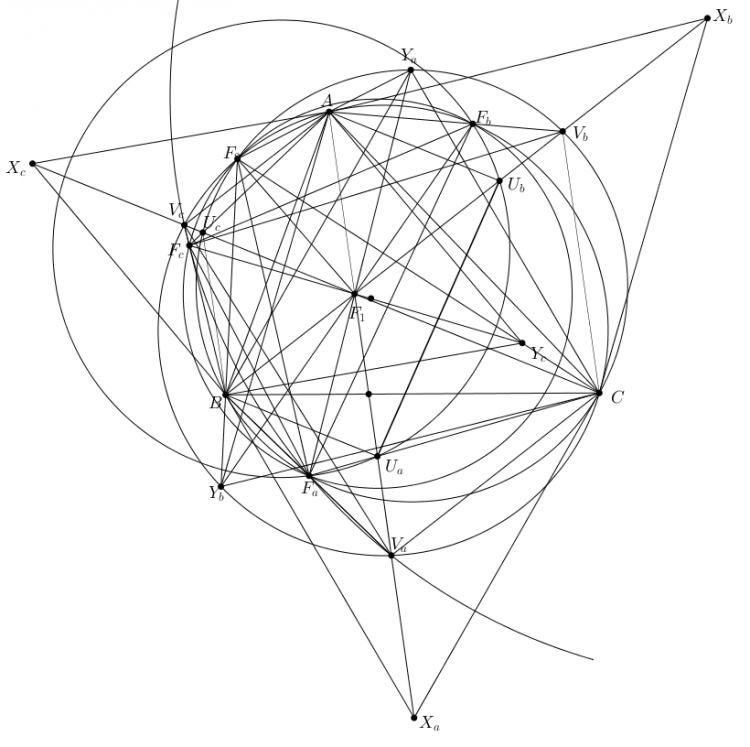
Bài viết đã được chỉnh sửa nội dung bởi manhtuan00: 06-05-2017 - 11:04